2022-2023学年冀教版数学九年级上册25.5相似三角形的性质同步测试题
试卷更新日期:2022-08-31 类型:同步测试
一、单选题
-
1. 已知两个相似三角形的周长比为 , 若较大三角形的面积等于 , 则较小三角形的面积等于( )A、 B、 C、 D、2. 如图,在矩形ABCD中,AB=2BC,点M是CD边的中点,点E,F分别是边AB,BC上的点,且AF⊥ME,G为垂足.若EB=2,BF=1,则四边形BFGE的面积为( )
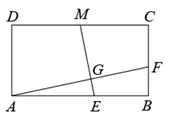 A、 B、 C、 D、3. 如图, 中, 是 的中位线,连接 , 相交于点 ,若 ,则 为( )
A、 B、 C、 D、3. 如图, 中, 是 的中位线,连接 , 相交于点 ,若 ,则 为( )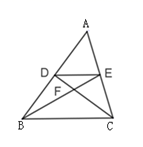 A、3 B、4 C、9 D、124. 如图,在 ABC中,DE BC,EF AB,下列等式成立的是( )
A、3 B、4 C、9 D、124. 如图,在 ABC中,DE BC,EF AB,下列等式成立的是( )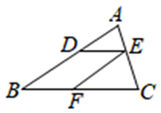 A、 B、 C、 D、5. 已知 ,且相似比为 ,则 与 的周长比为( )A、 B、 C、 D、6. 如图,在△ABC中,DE∥BC, = ,则下列结论中正确的是( )
A、 B、 C、 D、5. 已知 ,且相似比为 ,则 与 的周长比为( )A、 B、 C、 D、6. 如图,在△ABC中,DE∥BC, = ,则下列结论中正确的是( )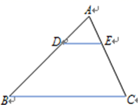 A、 B、 C、 D、7. 如果两个相似三角形的周长比为 , 那么它们的对应角平分线的比为( )A、 B、 C、 D、8. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ABC的面积为16,则四边形BCED的面积为( )
A、 B、 C、 D、7. 如果两个相似三角形的周长比为 , 那么它们的对应角平分线的比为( )A、 B、 C、 D、8. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ABC的面积为16,则四边形BCED的面积为( )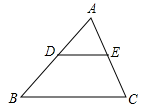 A、8 B、12 C、14 D、169. 如果两个相似三角形的面积比是4:9,则它们对应边上的高之比为( )A、4:9 B、16:81 C、2:3 D、3:210. 如果两个相似三角形的对应边之比为2:5,其中一个三角形的一个内角的角平分线长为7,则另一个三角形对应角平分线的长为( )A、 B、 C、 或 D、无法确定
A、8 B、12 C、14 D、169. 如果两个相似三角形的面积比是4:9,则它们对应边上的高之比为( )A、4:9 B、16:81 C、2:3 D、3:210. 如果两个相似三角形的对应边之比为2:5,其中一个三角形的一个内角的角平分线长为7,则另一个三角形对应角平分线的长为( )A、 B、 C、 或 D、无法确定二、填空题
-
11. 已知△ABC∽△DEF,相似比为3,则它们的周长之比是.12. 若将△ABC的各边都扩大为原来的2倍,则该三角形的周长会扩大为原来的倍.13. 如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,如果BC=2AD,那么S△AOD:S△BOC的值为.
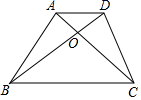 14. 如果两个相似三角形的周长比为2:3,那么它们的对应高的比为 .15. 如果两个相似三角形的面积比为1:4,其中较大三角形的周长为18,那么较小三角形的周长是 .16. 若两个相似三角形的相似比是5:7,则它们的对应高线的比是 .
14. 如果两个相似三角形的周长比为2:3,那么它们的对应高的比为 .15. 如果两个相似三角形的面积比为1:4,其中较大三角形的周长为18,那么较小三角形的周长是 .16. 若两个相似三角形的相似比是5:7,则它们的对应高线的比是 .三、解答题
-
17. 已知△ABC∽△DEF,且DE=2 cm,AB=4 cm,BC=5 cm,CA=6 cm,求△DEF的周长.18. 已知 和 中,有 ,且 和 的周长之差为15厘米,求 和 的周长.19. 已知△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比为k.(1)、如果CD和C′D′是它们的对应高,那么 等于多少?(2)、如果CD和C′D′是它们的对应角平分线,那么 等于多少?如果CD和C′D′是它们的对应中线呢?
四、综合题
-
20. 如图,AD和BC相交于点E,AC∥BD,点F在CD上,AC=4,BD=6, ,
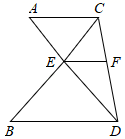 (1)、求EF的长;(2)、已知S△CBD=25,求△CEF的面积.21. [探索规律]
(1)、求EF的长;(2)、已知S△CBD=25,求△CEF的面积.21. [探索规律]如图①,在△ABC中,点D、E、F分别在AB、 BC、 AC上,且DF//BC,EF//AB.设△ADF的边DF上的高为h1 , △EFC的边CE上的高为h2.
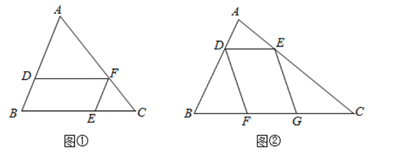 (1)、若△ADF、△EFC的面积分别为4和1,则 =;(2)、某校数学兴趣小组的同学对△ADF、△EFC、四边形BDEF的面积关系进行了研究设△ADF、△EFC、四边形BDEF的面积分别为S1、 S2、S, EC的长为a,则S2= (用含a和h2的式子表示);S1= (用含a、h1和h2的式子表示);S=(用含a、h1的式子表示);从而得出S=2 .(3)、[解决问题]
(1)、若△ADF、△EFC的面积分别为4和1,则 =;(2)、某校数学兴趣小组的同学对△ADF、△EFC、四边形BDEF的面积关系进行了研究设△ADF、△EFC、四边形BDEF的面积分别为S1、 S2、S, EC的长为a,则S2= (用含a和h2的式子表示);S1= (用含a、h1和h2的式子表示);S=(用含a、h1的式子表示);从而得出S=2 .(3)、[解决问题]如图②,在△ABC中,点D、E分别在AB、AC上,点F、G在BC上,且DE//BC,DF//EG.若△ADE、△DBF.△EGC的面积分别为2、3、 5,求△ABC的面积.