2022年苏科版初中数学七年级上册 2.8 有理数的混合运算同步练习

试卷更新日期：2022-08-30 类型：同步测试

进入出卷网下载

一、夯实基础

1. 下列计算中，正确的是（）

A、 $\frac{1}{2} - \frac{1}{2} \times 3 = 0 \times 3 = 0$ B、 $74 - 2^{2} \div 70 = 70 \div 70 = 1$ C、 $6 \div (\frac{3}{2} - \frac{2}{3}) = 6 \div \frac{5}{6} = \frac{36}{5}$ D、 ${(- 3)}^{2} - {(- 2)}^{3} = 9 - 8 = 1$

查看试题解析
2. 用2，0，2，2这四个数进行如下运算，计算结果最小的式子是 $($ $)$

A、 $2 - 0 \times 2 + 2$ B、 $2 - 0 + 2 \times 2$ C、 $2 \times 0 + 2 - 2$ D、 $2 + 0 - 2 \times 2$

查看试题解析
3. 在算式3-|-1□2|中的“□”里，选择一个运算符号，使得算式的值最大（）

A、+ B、- C、× D、÷

查看试题解析
4. 某地区每升高100米，气温降低0.6℃，测得地面气温为0℃，问550米的高空的气温为多少摄氏度？（）

A、33℃ B、－33℃ C、3.3℃ D、－3.3℃

查看试题解析
5. 某校规定英语竞赛成绩85分以上为优秀，老师将85分记为0，并将一组5名同学的成绩简记为−3，+14，0，+5，−6，这5名同学的平均成绩是（）

A、83 B、87 C、82 D、84

查看试题解析
6. 计算：

(1)、 $- 3^{2} - (- 8) \times {(- 1)}^{5} \div {(- 1)}^{4}$ ；

(2)、 $- 1^{2} + {(- 1 \frac{1}{2})}^{3} \div \frac{3}{4} - | 0.25 - \frac{3}{8} |$

(3)、 $(\frac{2}{3} - \frac{3}{4} + \frac{1}{6}) \div (- \frac{1}{24})$

查看试题解析
7. 计算： ${(- \frac{2}{3})}^{2} =$ ； $(\frac{1}{4} + \frac{1}{6} - \frac{1}{2}) \times 12 =$ ； $(- \frac{6}{25}) \div \frac{3}{5} =$ .

查看试题解析
8. 计算（ $1 \frac{3}{4} - \frac{7}{8} - \frac{7}{12}$ ）÷（﹣ $\frac{7}{8}$ ）+ $\frac{8}{7}$ ÷（ $1 \frac{3}{4} - \frac{7}{8} - \frac{7}{12}$ ）的结果为.

查看试题解析
9. 一只蚂蚁由数轴上表示 $- 2$ 的点先向右爬3个单位长度，再向左爬5个单位长度，则此蚂蚁所在的位置表示的数是．

查看试题解析
10. 定义“*”是一种运算符号，规定 $a * b = 3 a - 2 b + 2042$ ，则 $(- 4) * 5$ 的值为.

查看试题解析
11. 已知a、b互为倒数，c、d互为相反数， $| m | = 5$ ，n是最大的负整数.求代数式 ${(- a b)}^{2020} - 4 (c + d) - n + m^{2}$ 的值.

查看试题解析
12. 气象统计资料表明，高度每增加1000米，气温就降低大约5℃，我省著名风景区庐山的最高峰高于地面约为1200米，若现在地面温度约为3℃，则山顶气温大约是多少？

查看试题解析
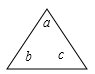13. 若“三角” 表示适算a+b+c，“方框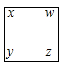表示运算x-y+z+w.
求：表示的速算，并计算结果。

查看试题解析
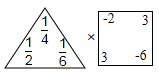14. “ $24$ ”点游戏的规则是这样的：在整数范围内任意取四个数，然后进行加、减、乘、除四则运算（每个数只能用一次，可使用小括号、中括号），使其结果等于 $24$ ．例如，取 $2$ ， $3$ ， $6$ ， $9$ 这四个数进行运算，得： $2 \times 6 + 3 + 9 = 24$ ，或 $6 \times 9 \div 2 - 3 = 24$ ，或 $3 \times 9 - 6 \div 2 = 24$ 等．

(1)、用-3，-1，5，3这四个整数，写出 $1$ 种算式，使其运算结果为24；

(2)、用 $- 6$ ， $3$ ， $4$ ， $10$ 这四个整数，写出 $2$ 种不同的算式，使其运算结果为24；

(3)、用 $- 4$ ， $2$ ， $8$ ， $11$ 这四个整数，写出 $1$ 种算式，使其运算结果为 $24$ ．

查看试题解析
15. 某出租车沿南北方向行驶，从A地出发，晚上到达B地．规定向北为正方向．行驶记录如下（单位：㎞）：+18、-9、+7、-14、-6、+13、-6，

(1)、B地在A地的什么位置？

(2)、若出租车每行驶1㎞耗油1升，求该天共耗油多少升？

(3)、若出租车起步价为7元，起步里程为3千米（包括3千米），超过部分每千米1.2元，则该天车费多少元？

查看试题解析

二、能力提优

16. 下列计算正确的是（）

A、 $- 1^{2} - (- 2) \times 3 = 7$ B、 $3 \div 4 \times \frac{1}{4} = 3$ C、 $5 \times (- 2) - {(- 1)}^{2} = 9$ D、 ${(- 1)}^{10} - 8 \div (- 2) + 4 \times (- 5) = - 15$

查看试题解析
17. 在某一段时间里，计算机按如图所示的程序工作，若输入的数为 $- 5$ ，则输出的数为（）

A、15 B、135 C、-135 D、615

查看试题解析
18. 一根木料锯成3段需6分钟，如果锯成6段需要的时间是（）

A、15分钟 B、9分钟 C、12分钟 D、16分钟

查看试题解析
19. 某商贩在一次买卖中，同时卖出两件上衣，每件都以60元出售，若按成本计算，其中一件赢利25%，另一件亏本25%，在这次买卖中，该商贩（）

A、不盈不亏 B、盈利8元 C、亏损8元 D、盈利10元

查看试题解析
20. $2021$ 减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ，....，以此类推，一直减到余下的 $\frac{1}{2021}$ ，则最后剩下的数是（）

A、 $0$ B、 $1$ C、 $\frac{2020}{2021}$ D、 $\frac{2021}{2020}$

查看试题解析
21. 如图，已知正方形的边长为24厘米，甲，乙两动点分别从正方形ABCD的顶点D，B同时沿正方形的边开始移动，甲点按顺时针方向环行，乙点按逆时针方向环行，若乙的速度为9厘米/秒，甲的速度为3厘米/秒，当它们运动了2022秒时，它们在正方形边上相遇了（）

A、252 次 B、253次 C、254次 D、255次

查看试题解析
22. 水池 $A, B, C$ 都是长方体，深为 $1.6 m$ ，底部尺寸为 $3 m \times 4 m$ .1号阀门 $24 min$ 可将无水A池注满；2号阀门用来从A池向B池放水， $30 min$ 可将A池中满池水放入B池；3号阀门用来从B池向C池放水， $48 \min$ 可将B池中满池水放入C池.若开始 $A 、 B 、 C$ 三池无水，同时打开1号、2号和3号阀门，那么当B池水深 $0.4 m$ 时，A池有（） $m^{3}$ 的水.

A、1.2 B、3.2 C、6 D、16

查看试题解析
23. 计算： $\frac{1}{63} \div (- 1 \frac{1}{7} + \frac{4}{9} - \frac{1}{3})$ ＝；

查看试题解析
24. 某魔术师的魔术表演风靡全国，小明也学起了某魔术师发明了一个魔术盒，当任意实数对（a，b）进入其中时，会得到一个新的实数：a²+b﹣1，例如把（3，﹣2）放入其中，就会得到3²+（﹣2）﹣1＝6.现将实数对（﹣1，3）放入其中，得到实数m，再将实数对（m，1）放入其中后，得到实数是.

查看试题解析
25. 我们常用的十进制数，如 $2639=2 \times 10^{3} +6 \times 10^{2} +3 \times 10^{1} +9$ ，我国古代《易经》一书记载，远古时期，人们通过在绳子上打结来记录数量，如图，一位母亲在如下排列的绳子上打结，并采用七进制（如 $2513=2 \times 7^{3} +5 \times 7^{2} +1 \times 7^{1} +3$ ），用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（）

A、1326天 B、510天 C、336天 D、84天

查看试题解析
26. 计算：

(1)、 $10 - (- 5) + (- 9)$

(2)、 $(- \frac{1}{6} + \frac{2}{3} - \frac{5}{12}) \div (- \frac{1}{48})$

(3)、 $- 1^{2021} - \frac{1}{6} \div (- 3 \times \frac{1}{9}) + | - 2 |$

查看试题解析
27. 定义运算“ $*$ ”：对于任意有理数a和b，规定 $a * b = b^{2} - a b - 3$ ，如 $2 * 3 = 3^{2} - 2 \times 3 - 3 = 0$ .

(1)、求 $- 5 * (- 3)$ 的值；

(2)、若 $(a - 3) * (- \frac{3}{4}) = a - 1$ ，求a的值.

查看试题解析

三、延伸拓展

28. 已知，如图，点A对应的数为2 .

(1)、点B在点A左边，距离点A 6个单位长度，则点B对应的数为

(2)、若点C距点A 10个单位长度，则点C所对应的数为

(3)、在（1）的条件下，点A与点 B之间(包括 A，B 两点)所有的非正整数之和为

(4)、在（1）的条件下A，B 两点同时运动，点A以每秒2个单位长度的速度沿数轴向左运动，点B以每秒3个单位长度的速度向右运动，当点A运动到-4所在的点，点B运动到的点对应的数为

(5)、在（1）的条件下，点A 静止不动，点 B以每秒3个单位长度的速度向右运动，经过多长时间 A，B两点之间相距3个单位长度?

查看试题解析
29. 某超市对顾客实行优惠购物，规定如下：
（1）若一次性购物不超过100元，则不予优惠；
（2）若一次性购物超过100元，但不超过300元，按标价给予九折优惠；
（3）若一次性购物超过300元，其中300元以下部分（包括300元）给予九折优惠；超过300元部分给予八折优惠.
小李两次去该超市购物，分别付款99元和252元.现在小张决定一次性购买小李分两次购买的物品，他需付款多少元?

查看试题解析
30. 问题探索：如图，将一根木棒放在数轴（单位长度为1cm）上，木棒左端与数轴上的点A重合，右端与数轴上的点B重合.

(1)、若将木棒沿数轴向右水平移动，则当它的左端移动到点B时，它的右端在数轴上所对应的数为30；若将木棒沿数轴向左水平移动，则当它的右端移动到点A时，它的左端在数轴上所对应的数为6，由此可得这根木棒的长为cm.

(2)、图中点A所表示的数是，点B所表示的数是.

(3)、实际应用：由（1）（2）的启发，请借助“数轴”这个工具解决下列问题：
一天，妙妙去问奶奶的年龄，奶奶说：“我若是你现在这么大，你还要35年才出生；你若是我现在这么大，我就115岁啦! ”请问妙妙现在多少岁了？

查看试题解析

2022年苏科版初中数学七年级上册 2.8 有理数的混合运算 同步练习

一、夯实基础

二、能力提优

三、延伸拓展

2022年苏科版初中数学七年级上册 2.8 有理数的混合运算同步练习