广东省珠海市2022届高三上学期数学期末考试试卷

试卷更新日期：2022-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | - 1 < x < 2}$ ， $B = [0 ， 4)$ ，则 $A ∪ B =$ （）

A、 $(- 1 ， + \infty)$ B、 $(- 1 ， 4)$ C、 $(0 ， 4)$ D、 $(1 ， 4)$

查看试题解析
2. 若复数 $z = \frac{2 + i}{2 - i}$ ，则 $| z | =$ （）

A、1 B、3 C、 $\sqrt{5}$ D、5

查看试题解析
3. 设 $a = l o g_{3} π$ ， $b = l o g_{2} 3$ ， $c = 0 . 2^{0.3}$ ，则a，b，c大小关系为（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > b > a$ D、 $c > a > b$

查看试题解析
4. 数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， a $2 = 2$ 且 $a_{n + 2} = a_{n} + {(- 1)}^{n}$ ， $n \in N^{*}$ ，则该数列的前40项之和为（）

A、-170 B、80 C、60 D、230

查看试题解析
5. 已知 $f (x)$ 是定义域在 $R$ 上的奇函数，且满足 $f (x + 1) = f (x - 1)$ ．当 $x \in (0 ， 1)$ 时， $f (x) = 2^{x} + 1$ ，则 $f (l o g_{2} 3) =$ （）

A、 $- \frac{7}{3}$ B、 $\frac{7}{3}$ C、4 D、-4

查看试题解析
6. 在 $△ A B C$ 中， $A B = \sqrt{2}$ ， $∠ A B C = \frac{π}{4}$ ， $B C = 3$ ， $A D$ 为 $B C$ 边上的高；O为 $A D$ 上靠近点A的三等分点，且 $\vec{A O} = λ \vec{A B} + μ \vec{A C}$ ，其中 $λ$ ， $μ \in R$ ，则 $λ - μ =$ （）

A、 $\frac{1}{2}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、 $\frac{1}{3}$

查看试题解析
7. 双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 的右支上一点M关于原点O的对称点为点N，F为双曲线的右焦点，若 $M O = O F$ ， $∠ F M N = \frac{π}{3}$ ，则双曲线C的离心率e为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{2} + 1$ D、 $\sqrt{3} + 1$

查看试题解析
8. 已知 $f (x) = x^{2} - (a + 2) x e^{x - 1} + (a + 1) e^{2 (x - 1)}$ 恰有三个不同的零点，则实数a的范围为（）

A、 $(0 ， 1)$ B、 $(- 1 ， 1)$ C、 $(0 ， e)$ D、 $(- 1 ， 0)$

查看试题解析

二、多选题

9. 以下结论正确的是（）

A、两个随机变量的线性相关性越强，则相关系数r的绝对值越接近于1 B、在检验A与B是否有关的过程中，根据数据算得 $K^{2}$ 的值， $K^{2}$ 越小，认为“A与B有关”的把握越小 C、随机变量 $X ~ B (n ， p)$ ，若 $E (X) = 30$ ， $D (X) = 20$ ，则 $n = 45$ D、在残差图中，残差点分布的水平带状区域越窄，说明模型的拟合效果越好

查看试题解析
10. 关于函数 $f (x) = 2 s i n (2 x + \frac{π}{4})$ ，下列说法正确的是（）

A、函数 $y = f (x)$ 的图象可由函数 $y = 2 s i n 2 x$ 的图象向左平移 $\frac{π}{4}$ 个单位得到 B、 $y = f (x)$ 的图象关于直线 $x = - \frac{3 π}{8}$ 对称 C、 $y = f (x)$ 的表达式可以改写为 $f (x) = - 2 c o s (2 x - \frac{π}{4})$ D、若函数 $f (x)$ 在 $[- \frac{π}{4} ， m]$ 的值域为 $[- \sqrt{2} ， 2]$ ，则m的取值范围是 $[\frac{π}{8} ， \frac{π}{2}]$

查看试题解析
11. 已知O为坐标原点，M为平面上一动点，且满足 $O M = 1$ ．若M的轨迹为曲线C，点P在直线 $l ： 2 x + y - 3 = 0$ 上，过点P作曲线C的两条切线，A、B是切点．下列结论中错误的为（）

A、曲线C上不存在到直线l的距离为1的点 B、切线长 $P A$ 的最小值为 $\frac{2 \sqrt{5}}{5}$ C、直线l上存在点P，使 $∠ A P B = 50 °$ D、四边形 $P A O B$ 面积的最小值为1

查看试题解析
12. 如图，在直棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，各棱长均为2， $∠ A B C = \frac{π}{3}$ ，则下列说法正确的是（）

A、三棱锥 $A_{1} - A B C$ 外接球的表面积为 $\frac{28}{3} π$ B、异面直线 $A B_{1}$ 与 $B C_{1}$ 所成角的余弦值为 $\frac{1}{2}$ C、当点M在棱 $B B_{1}$ 上运动时， $| M D | + | M A_{1} |$ 最小值为 $2 \sqrt{5 + 2 \sqrt{3}}$ D、N是平面 $A B C D$ 上一动点，若N到直线 $A A_{1}$ 与 $B C$ 的距离相等，则N的轨迹为抛物线

查看试题解析

三、填空题

13. 非负实数x，y满足 $2 x y - x - 6 y = 0$ ，则 $x + 2 y$ 的最小值为．

查看试题解析
14. 若函数 $f (x) = l n x + \frac{a}{x}$ 在 $x = 1$ 处的切线与直线 $x + 2 y - 1 = 0$ 垂直，则 $a =$ ．

查看试题解析
15. 接种疫苗是预防控制新冠疫情最有效的方法．我国自2021年1月9日起实施全民免费接种新冠疫苗．截止到2021年5月底，国家已推出了三种新冠疫苗（腺病毒载体疫苗、新冠病毒灭活疫苗、重组新冠病毒疫苗）供接种者选择，每位接种者任选其中一种．若5人去接种新冠疫苗，恰有3人接种同一种疫苗的概率为．

查看试题解析
16. 在数列 ${a_{n}}$ 中，给定 $a_{1}$ ，且函数 $f (x) = \frac{1}{3} x^{3} - a_{n + 1} s i n x + (a_{n} + 2) x + 1$ 的导函数有唯一的零点，则 $a_{2} - a_{1} =$ ；设函数 $g (x) = 8 x + s i n (π x) - c o s (π x)$ 且 $g {(a)}_{1} + g (a_{2}) + \cdot \cdot \cdot + g (a_{9}) = 18$ ，则 $a_{5} =$ ．

查看试题解析

四、解答题

17. 等差数列 ${a_{n}}$ 前n项和为 $S_{n}$ ，且 $a_{3} + a_{6} = 16$ ， $S_{9} = 81$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设数列 ${\frac{1}{a_{n + 1} a_{n + 2}}}$ 的前n项和为 $T_{n}$ ，若 $T_{n} > \frac{2}{15}$ ，求n的最小值．

查看试题解析
18. 在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c，且 $a = b (\sqrt{3} s i n C + c o s C)$ ．

(1)、求B；

(2)、已知 $B C = 2 \sqrt{3}$ ， D为边 $A B$ 上的一点，若 $B D = 1$ ， $∠ A C D = \frac{π}{2}$ ，求 $A C$ 的长．

查看试题解析
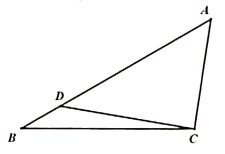19. 为建设粤港澳大湾区教育高地，办人民满意的教育，深入推进基础教育课堂教学改革，某高中为了提升教育质量，探索了一种课堂教学改进项目．某研究机构为了解实施新项目后的教学效果，通过随机抽样调查了该校某年级100位学生，对这些学生的课堂测试成绩进行统计，得到样本的频率分布直方图，如图所示．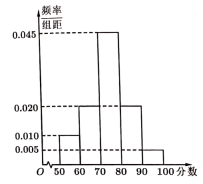
附参考数据：若 $X ~ N (μ ， σ^{2})$ ，则 $P (μ - σ < X \leq μ + σ) = 0.6827$ ； $P (μ - 2 σ < X \leq μ + 2 σ) = 0.9545$ ； $P (μ - 3 σ < X \leq μ + 3 σ) = 0.9973$ ．

(1)、若这些学生课堂测试成绩的分数X近似地服从正态分布 $N (μ ， 100)$ ，其中 $μ$ 近似为样本平均数 $\bar{x}$ （同一组数据用该组数据区间的中点值表示），求 $P (64 < X \leq 94)$ ；

(2)、为做进一步了解，研究机构采用分层抽样的方法从课堂测试成绩位于分组 $[50 ， 60)$ ， $[60 ， 70)$ ， $[80 ， 90)$ 的学生中抽取10人，再从中任选3人进行调查，求抽到分数位于 $[80 ， 90)$ 的人数 $ξ$ 的分布列和数学期望．

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，四边形 $A B C D$ 为平行四边形，P在平面 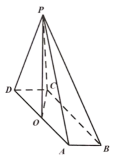$A B C D$ 的投影为边 $A D$ 的中点O， $∠ A B C = \frac{π}{3}$ ， $B C = 4$ ， $A B = 1$ ， $P O = 3$ ．

(1)、求证： $A B ⊥$ 平面 $P O C$ ；

(2)、在线段 $P B$ 上，是否存在一点E，使得平面 $P O C$ 与平面 $E O C$ 的夹角的余弦值为 $\frac{3 \sqrt{10}}{10}$ ，若存在，指明点E的位置，若不存在，说明理由．

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的长轴长为4，左顶点A到上顶点B的距离为 $\sqrt{5}$ ， F为右焦点．

(1)、求椭圆C的方程和离心率；

(2)、设直线l与椭圆C交于不同的两点M，N（不同于A，B两点），且直线 $B M ⊥ B N$ 时，求F在l上的射影H的轨迹方程．

查看试题解析
22. 已知函数 $f (x) = e^{x} - k s i n (2 x)$ 在区间 $(0 ， \frac{π}{4})$ 内存在极值点 $α$ ．

(1)、求实数k的取值范围；

(2)、求证：在区间 $(0 ， \frac{π}{2})$ 内存在唯一的 $β$ ，使 $f (β) = 1$ ，并比较 $β$ 与 $2 α$ 的大小．

查看试题解析