北京市顺义区2022届高三上学期数学期末考试试卷

试卷更新日期：2022-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 在复平面内，复数 $z = \frac{2 i}{1 - i}$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 集合 $A = {- 2 ， - 1 ， 0}$ ， $B = {x | x^{2} \leq 1}$ ，则 $A ∩ B =$ （）

A、{-1} B、 ${- 1 ， 0}$ C、 ${- 2 ， - 1}$ D、 ${- 2 ， 0}$

查看试题解析
3. 下列函数中，既是奇函数又在区间 $(0 ， 1)$ 上单调递增的是（）

A、 $y = \frac{1}{x}$ B、 $y = 2^{x}$ C、 $y = l o g_{2} x$ D、 $y = s i n x$

查看试题解析
4. 已知 $| \vec{a} | = | \vec{b} | = 1$ ，且 $\vec{a} ⊥ (\vec{a} + 3 \vec{b}) ，$ 则向量 $\vec{a} ， \vec{b}$ 夹角的余弦值为（）

A、 $- \frac{1}{3}$ B、 $- \frac{1}{5}$ C、 $\frac{1}{5}$ D、 $\frac{1}{3}$

查看试题解析
5. 在等差数列 ${a_{n}}$ 中， $a_{7} - a_{3} = 2$ ， $a_{4} = 1$ ，则 $a_{12} =$ （）

A、5 B、4 C、3 D、2

查看试题解析
6. 设 $x \in R$ ，则“ $\frac{1}{x} < 1$ ”是“ $x > 1$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 已知过 $B D_{1}$ 的平面与正方体 $A B C D$ 相交，分别交棱 $A A_{1}$ ， $C C_{1}$ 于 $M$ ， $N$ .则下列关于截面 $B M D_{1} N$ 的说法中，不正确的是（）

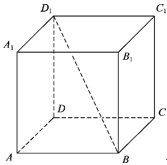A、截面 $B M D_{1} N$ 可能是矩形 B、截面 $B M D_{1} N$ 可能是菱形 C、截面 $B M D_{1} N$ 可能是梯形 D、截面 $B M D_{1} N$ 不可能是正方形

查看试题解析
8. 已知两点 $M (- 5 ， 0)$ ， $N (5 ， 0)$ ，若直线上存在点P，使得 $| P M | - | P N | = 8$ 成立，则称该直线为“单曲直线”.下列直线中，“单曲直线”是（）
① $y = x + 2$ ；② $x = 4$ ；③ $y = \frac{3}{4} x$ ；④ $y = \frac{1}{2} x - 1$

A、①② B、①③ C、②③ D、②④

查看试题解析
9. 如图，△ $O B_{1} A_{1}$ ， △ $A_{1} B_{2} A_{2}$ 是全等的等腰直角三角形， $B_{1} ， B_{2}$ 为直角顶点， $O ， A_{1} ， A_{2}$ 三点共线.若点 $P_{1} ， P_{2}$ 分别是边 $A_{1} B_{1} ， A_{2} B_{2}$ 上的动点（不包含端点）.记 $m = \vec{O B_{1}} \cdot \vec{O P_{2}}$ ， $n = \vec{O B_{2}} \cdot \vec{O P_{1}}$ ，则（）

A、 $m > n$ B、m＜n C、m=n D、 $m ， n$ 大小不能确

查看试题解析
10. 为弘扬传统文化，某中学举办了主题为“琴、棋、书、画”的传统文化知识竞赛.现有四位选手进入到决赛.决赛按“琴、棋、书、画”的主题分为四个环节，规定每个环节的第一名到第四名的得分依次为4，3，2，1分，四个环节结束后统计总分.若总分第一名获得14分，总分第二名获得13分.有下列结论：①总分第三名不超过9分；②总分第四名可能在某一个环节的比赛中拿到3分；③总分第四名不超过6分；④总分第三名可能获得某一个环节比赛的第一名.其中，所有正确结论的序号是（）

A、①② B、①④ C、①②③ D、②③④

查看试题解析

二、填空题

11. 函数 $f (x) = \sqrt{2 - x} + lg (x + 1)$ 的定义域为.

查看试题解析
12. ${(x^{2} + \frac{1}{x})}^{5}$ 展开式中 $x$ 的系数为.（用数字作答）

查看试题解析
13. 若实数 $a ， b$ 满足 $a = b - 1$ ，则使得 $0 < a b < 2$ 成立的一个 $a$ 的值是.

查看试题解析
14. 城市的许多街道是相互垂直或平行的，因此，乘坐出租车往往不能沿直线到达目的地，只能按直角拐弯的方式行走.在平面直角坐标系中，定义 $d (P ， Q) = | x_{1} - x_{2} | + | y_{1} - y_{2} |$ 为两点 $P (x_{1} ， y_{1})$ 、 $Q (x_{2} ， y_{2})$ 之间的“出租车距离”.
给出下列四个结论：①若点 $O (0 ， 0)$ ，点 $A (1 ， 2)$ ，则 $d (O ， A) = 3$ ；
②到点 $O (0 ， 0)$ 的“出租车距离”不超过 $1$ 的点的集合所构成的平面图形面积是 $π$ ；
③若点 $A (1 ， 2)$ ，点 $B$ 是抛物线 $y^{2} = x$ 上的动点，则 $d (A ， B)$ 的最小值是 $1$ ；
④若点 $A (1 ， 2)$ ，点 $B$ 是圆 $x^{2} + y^{2} = 1$ 上的动点，则 $d (A ， B)$ 的最大值是 $3 + \sqrt{2}$ .
其中，所有正确结论的序号是.

查看试题解析
15. 将直线 $l ：$ $x - y + 2 = 0$ 绕着点 $A (1 ， 3)$ 按逆时针方向旋转 $1 5^{∘}$ ，得到直线 $l_{1}$ .则 $l_{1}$ 的倾斜角为， $l_{1}$ 的方程是.

查看试题解析

三、解答题

16. 如图，在长方体 $A B C D$ 中， $A D = A A_{1} = 1 ， A B = 2$ ，点 $E$ 在线段AB上.

(1)、证明： $A_{1} D ⊥ D_{1} E$ ；

(2)、当点 $E$ 是AB中点时，求 $A_{1} D$ 与平面 $D_{1} E C$ 所成角的大小.

查看试题解析
17. 在 $△ A B C$ 中， $a = 1$ ， $c s i n A = \sqrt{3} a c o s C$ .

(1)、求 $C$ 的大小；

(2)、再从条件①、条件②、条件③这三个条件中选择一个作为已知，判断 $△ A B C$ 是否存在，若不存在，说明理由；若存在，求出 $△ A B C$ 的面积.条件①： $c o s A c o s C = \frac{\sqrt{2}}{4}$ ；条件②： $b^{2} - c^{2} = a c$ ；条件③： $a ， b ， c$ 成等差数列.注：如果选择多个符合要求的条件分别解答，按第一个解答计分.

查看试题解析
18. 某单位4人积极参加本地区农产品的网购活动，共有 $A 、 B$ 两种农产品供选择，每人只购其中一种.大家约定：每人通过掷一次质地均匀的骰子决定自己去购买哪种农产品.若掷出点数为1或2，购买农产品A，若掷出点数大于2，则购买农产品B.

(1)、求这4个人中恰有1人购买农产品A的概率；

(2)、用 $ξ ， η$ 分别表示这4个人中购买农产品A和B的人数，记 $X = ξ η$ ，求随机变量 $X$ 的分布列与数学期望 $E (X)$ .

查看试题解析
19. 已知函数 $f (x) = \frac{1}{2} a x + \frac{a - 2}{2 x} (a > 0)$ .

(1)、若 $a = 1$ ，求曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、若对任意 $x \in [1 ， + ∞)$ ，都有 $f (x) \geq l n x$ ，求实数 $a$ 的取值范围.

查看试题解析
20. 已知椭圆 $W ：$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 过点 $A (0 ， - 1)$ ，且离心率 $e = \frac{\sqrt{3}}{2}$ .

(1)、求椭圆 $W$ 的方程；

(2)、点 $B$ 在直线 $x = 4$ 上，点 $B$ 关于 $x$ 轴的对称点为 $B_{1}$ ，直线 $A B$ 、 $A B_{1}$ 分别交椭圆 $W$ 于 $C$ 、 $D$ 两点（不同于 $A$ 点）.求证：直线 $C D$ 过定点.

查看试题解析
21. 数列 $A_{n}$ ： $a_{1} ， a_{2} ， ⋯ ， a_{n} (n \geq 2)$ 满足 $a_{i} \in {- 1 ， 1} ， (i = 1 ， 2 ， ⋯ ， n)$ ，称 $T_{n} = a_{1} \cdot 2^{n - 1} + a_{2} \cdot 2^{n - 2} + a_{3} \cdot 2^{n - 3} + ⋯ + a_{n - 1} \cdot 2^{1} + a_{n} \cdot 2^{0}$ 为数列 $A_{n}$ 的指数和.

(1)、若 $n = 3$ ，求 $T_{3}$ 所有可能的取值；

(2)、求证： $T_{n} < 0$ 的充分必要条件是 $a_{1} = - 1$ ；

(3)、若 $T_{100} < 0$ ，求 $T_{100}$ 的所有可能取值之和.

查看试题解析