天津市东丽区2021-2022学年高二下学期数学期末考试试卷

试卷更新日期：2022-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {0 ， 1 ， 2} ， B = {1 ， 2 ， 3}$ ，则 $A ∩ B =$ （）

A、 ${1 ， 2}$ B、 ${0 ， 1 ， 2}$ C、 ${1 ， 2 ， 3}$ D、 ${0 ， 1 ， 2 ， 3}$

查看试题解析
2. 在 ${(x - \frac{1}{x})}^{5}$ 的展开式中， $x^{3}$ 的系数为（）

A、-5 B、5 C、-10 D、10

查看试题解析
3. 已知 $a = 3^{- 2}$ ， $b = l o g_{0.4} 2$ ， $c = l o g_{2} 3$ ，则（）

A、 $a > b > c$ B、 $a > c > b$ C、 $b > c > a$ D、 $c > a > b$

查看试题解析
4. 已知 $x \in R$ ，则“ $x < - 2$ ”是“ $x^{2} + x - 2 > 0$ "的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 命题“ $\forall x \in R$ ， $x^{2} - 3 < 0$ ”的否定是（）

A、 $\forall x \in R$ ， $x^{2} - 3 > 0$ B、 $\forall x \in R$ ， $x^{2} - 3 \geq 0$ C、 $\exists x \in R$ ， $x^{2} - 3 > 0$ D、 $\exists x \in R$ ， $x^{2} - 3 \geq 0$

查看试题解析
6. 一箱产品中有8件正品和2件次品．每次从中随机抽取1件进行检测，抽出的产品不再放回．已知前两次检测的产品均是正品，则第三次检测的产品是正品的概率为（）

A、 $\frac{64}{125}$ B、 $\frac{7}{15}$ C、 $\frac{3}{4}$ D、 $\frac{1}{4}$

查看试题解析
7. 某校开展“迎奥运阳光体育”活动，共设踢毽、跳绳、拔河、推火车、多人多足五个集体比赛项目，各比赛项目逐一进行．为了增强比赛的趣味性，在安排比赛顺序时，多人多足不排在第一场，拔河排在最后一场，则不同的安排方案种数为（）

A、3 B、18 C、21 D、24

查看试题解析
8. 在下列4组样本数据的散点图中，样本相关系数最大的是（）

A、 $r_{1}$ B、 $r_{2}$ C、 $r_{3}$ D、 $r_{4}$

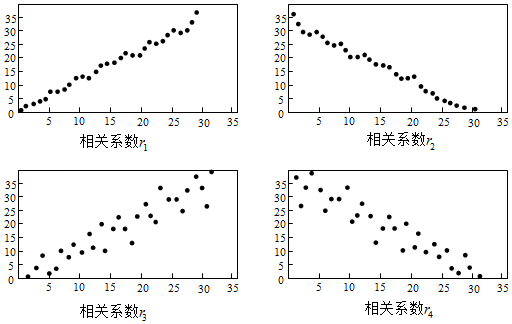查看试题解析
9. 已知函数f（x）的定义域为[－1，5]，其部分自变量与函数值的对应情况如下表：
x
－1
0
2
4
5
f（x）
3
1
2.5
1
3
f（x）的导函数 $f^{^{'}} (x)$ 的图象如图所示．给出下列四个结论：
①f（x）在区间[－1，0]上单调递增；②f（x）有2个极大值点；③f（x）的值域为[1，3]；④如果x∈[t，5]时，f（x）的最小值是1，那么t的最大值为4．
其中，所有正确结论的序号是（）

A、③ B、①④ C、②③ D、③④

查看试题解析

二、填空题

10. 已知 ${(2 + x)}^{n}$ 的展开式的二项式系数之和为16，则 $n =$ ；展开式的常数项是．

查看试题解析
11. 数列{ $a_{n}$ }是公比为2的等比数列，其前n项和为 $S_{n}$ 。若 $a_{2} = \frac{1}{2}$ ，则 $a_{n}$ =； $S_{5}$ =

查看试题解析
12. 从4名男生和2名女生中任选3人参加演讲比赛，则所选3人中至少有1名女生的概率是．

查看试题解析
13. 曲线 $f (x) = x^{3} + l n x$ 在点 $(1 ， 1)$ 处的切线方程为.

查看试题解析
14. 已知随机变量 $X ∼ N (1 ， σ^{2})$ ， $P (X \leq 2) = 0.84$ ，则 $P (X \leq 0) =$ ．

查看试题解析
15. 已知正数a，b满足 $a + b = 1$ ，则 $\frac{1}{a} + \frac{a}{b}$ 的最小值是.

查看试题解析

三、解答题

16. 已知函数 $f (x) = x^{3} + 3 x^{2} - a x$ 在x＝1处取得极值．

(1)、求a的值；

(2)、求f（x）在区间[－4，4]上的最大值和最小值．

查看试题解析
17. 某学校学生会有10名志愿者，其中高一2人，高二3人，高三5人，现从这10人中任意选取3人参加一个冬奥会志愿活动.

(1)、求选取的3个人来自同一年级的概率；

(2)、设 $X$ 表示选取的志愿者是高二学生的人数，求 $X$ 的分布列和期望.

查看试题解析
18. 教育部决定自2020年起，在部分高校开展基础学科招生改革试点（也称强基计划）．强基计划主要选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生，强基计划的校考由试点高校自主命题.已知甲、乙两所大学的笔试环节都设有三门考试科目，且每门科目是否通过相互独立．若某考生报考甲大学，每门科目通过的概率分别为 $\frac{1}{3}$ ， $\frac{2}{3}$ ， $\frac{1}{2}$ ，该考生报考乙大学，每门科目通过的概率均为 $\frac{2}{5}$ ．

(1)、设A为事件“该考生报考乙大学在笔试环节至少通过二门科目”求事件A发生的概率；

(2)、设X为该考生通过甲大学的笔试环节科目数，求随机变量X的分布列和数学期望．

查看试题解析
19. 已知等比数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， $a_{5} = \frac{1}{8} a_{2}$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、求数列 ${a_{n}}$ 的前n项和 $S_{n}$ ；

(3)、求数列 ${\frac{n}{a_{n}}}$ 的前n项和 $T_{n} .$

查看试题解析
20. 已知函数 $f (x) = e^{x} - a x$ ．

(1)、若 $f^{'} (0) = 0$ ，求 $f (x)$ 的极值

(2)、讨论 $f (x)$ 的单调区间；

(3)、对 $\forall x \in (0 ， + \infty)$ ，都有 $f (x) > 0$ 恒成立，求 $a$ 的取值范围．

查看试题解析

x	－1	0	2	4	5
f（x）	3	1	2.5	1	3