辽宁省大连市金普新区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是（）．

A、 $x \neq 2$ B、 $x = 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
2. 下列二次根式中，最简二次根式是（）．

A、 $\sqrt{\frac{1}{6}}$ B、 $\sqrt{6}$ C、 $\sqrt{12}$ D、 $\sqrt{36}$

查看试题解析
3. 下列各组数中能作为直角三角形的三边长的是（）

A、6，7，8 B、5，6，7 C、4.5，6，7.5 D、4，5，6

查看试题解析
4. 若平行四边形中两内角的度数比为2∶3，则其中较小的内角是（）．

A、36° B、45° C、60° D、72°

查看试题解析
5. 直线 $y = 3 x - 6$ 与x轴的交点坐标是（）．

A、 $(2 ， 0)$ B、 $(0 ， 2)$ C、 $(0 ， - 6)$ D、 $(- 6 ， 0)$

查看试题解析
6. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩平均数均为9环，方差分别为： $s_{甲}^{2} = 0.56$ ， $s_{乙}^{2} = 0.48$ ， $s_{丙}^{2} = 0.58$ ， $s_{丁}^{2} = 0.52$ ，则成绩最稳定的是（）．

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 四边形 $A B C D$ 是平行四边形，下列结论中正确的是（）

A、当 $A C = B D$ 时，它是菱形 B、当 $A C = B D$ 时，它是矩形 C、当 $A C = B D$ 时，它是正方形 D、当 $A C ⊥ B D$ 时，它是正方形

查看试题解析
8. 顺次连接菱形四边中点所得的四边形一定是（）

A、矩形 B、菱形 C、正方形 D、梯形

查看试题解析
9. 若一次函数的 $y = - 3 x + b$ 图象上有两点 $A (- 2 ， y_{1})$ ， $B (6 ， y_{2})$ ，则下列 $y_{1}$ ， $y_{2}$ 大小关系正确的是（）．

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} \geq y_{2}$ D、 $y_{1} \leq y_{2}$

查看试题解析
10. 如图，将矩形纸片ABCD折叠，使点C与点A重合，折痕为EF，若AB=4，BC=8.则D′F的长为（）

A、2 $\sqrt{5}$ B、4 C、3 D、2

查看试题解析

二、填空题

11. 一组数据：23，29，22，m，27，它的中位数是24，则这组数据的平均数是．

查看试题解析
12. 小明参加演讲比赛，演讲内容、演讲能力、演讲效果三个方面得分分别为85分、95分、95分，按演讲内容占50％、演讲能力占40％、演讲效果占10％计算成绩，则小明的成绩是分．

查看试题解析
13. 在平面直角坐标中，点 $A (- 3 ， - 2)$ 、 $B (- 1 ， - 2)$ ，直线 $y = k x (k \neq 0)$ 与线段AB有交点，则k的取值范围为．

查看试题解析
14. 如图，正方形ABCD的边长为4，点M在AB上，且 $A M = 1$ ， N是BD上一动点，则 $A N + M N$ 的最小值为．

查看试题解析
15. 如图，在菱形 $A B C D$ 中， $∠ B A D = 60 °$ ，点E在边 $B C$ 上，将 $△ A B E$ 沿直线 $A E$ 翻折180°，得到 $△ A B' E$ ，点B的对应点是点 $B^{'}$ 若 $A B^{'} ⊥ B D$ ， $B E = 2$ ，则 $B B^{'}$ 的长是．

查看试题解析
16. “五一黄金周”期间李师傅一家开车去旅游，出发前查看了油箱里有50升油，下面的两幅图分别描述了行驶里程及耗油情况，行驶130公里时，油箱里剩油量为升.

查看试题解析

三、解答题

17. 计算： ${(\sqrt{5} - 1)}^{2} + (\sqrt{3} + 2) (2 - \sqrt{3}) + \frac{10}{\sqrt{5}}$ ．

查看试题解析
18. 已知一次函数的图象过点 $(2 ， 3)$ 与 $(- 3 ， - 7)$ ．

(1)、求这个一次函数的解析式；

(2)、直接写出这个一次函数的图象与两坐标轴的交点坐标．

查看试题解析
19. 如图，已知四边形ABCD是平行四边形，BE∥DF，且分别交对角线AC于点E，F，连接DE，BF．求证：四边形DEBF是平行四边形．

查看试题解析
20. 如图，在四边形 $A B C D$ 中，已知 $∠ B = 90 °$ ， $A B = B C = 2 ， A D = 1 ， C D = 3$ .

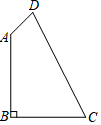(1)、求 $∠ D A B$ 的度数；

(2)、求四边形 $A B C D$ 的面积.

查看试题解析
21. 甲乙两名射击运动员10次射击训练成绩如下表（10环制）：
甲
7
10
9
7
8
10
9
10
10
10
乙
7
8
10
9
8
10
10
9
10
9

(1)、填空：甲运动员成绩的众数是环，乙运动员成绩的中位数是环；

(2)、计算甲运动员的平均成绩和方差．

查看试题解析
22. 下表给出A、B、C三种上宽带网的收费方式．
收费方式
月使用费/元
包时上网时间/h
超时费/（元/min）
A
30
25
0.05
B
50
50
0.05
C
120
不限时

(1)、设月上网时间为xh，方式A、B、C的收费金额分别为 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ ，直接写出 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的解析式，并写出自变量x的取值范围；

(2)、填空：①当上网时间时，选择方式A最省钱；
②当上网时间时，选择方式B最省钱；
③当上网时间时，选择方式C最省钱．

查看试题解析
23. 四边形 $A B C D$ 是正方形，点E是边 $B C$ 上的点（与B、C不重合）．点F在正方形外角 $∠ D C G$ 的平分线 $C H$ 上，且 $A E = E F$ ．求证： $∠ A E F = 90 °$ ．

查看试题解析
24. 如图，正方形ABCD的边长为6cm，P，Q两动点同时从点C出发，点P沿CB→BA以3cm/s的速度向终点A匀速运动，点Q沿CD→DB以2cm/s的速度向点B匀速运动，当点P到达终点A时，点Q同时停止运动．设点P的运动时间为t（s），△CPQ的面积为S（cm²）．

(1)、填空：点P的运动时间为 s；

(2)、求S关于t的函数解析式，并直接写出自变量t的取值范围．

查看试题解析
25. 如图，直线 $x = t$ 与直线 $y = - x$ 和直线 $y = \frac{1}{2} x + 2$ 分别交于点E，D（D在E的上方）．

(1)、直线 $y = - x$ 和直线 $y = \frac{1}{2} x + 2$ 交于点M，填空：点M的坐标为；

(2)、求线段DE的长（用含t的代数式表示）；

(3)、点N是y轴上一动点，且 $△ N D E$ 为等腰直角三角形，直接写出t的值及点N的坐标．

查看试题解析
26. 如图，点E，F，分别是正方形ABCD的边BC，CD的中点，AF与DE交于点G，连接BG．

(1)、写出线段AF与DE的数量关系和位置关系，并证明；

(2)、求证： $∠ B G E = ∠ D A F$ ．

查看试题解析

收费方式	月使用费/元	包时上网时间/h	超时费/（元/min）
A	30	25	0.05
B	50	50	0.05
C	120	不限时

甲	7	10	9	7	8	10	9	10	10	10
乙	7	8	10	9	8	10	10	9	10	9