辽宁省本溪市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-29 类型:期末考试
一、单选题
-
1. 若 , 则下列各式正确的是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
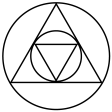 B、
B、 C、
C、 D、
D、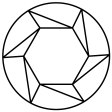 3. 下列因式分解正确的是( )A、 B、 C、 D、4. 一个多边形的内角和与外角和相等,这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形5. 如图,的对角线 , 相交于点O, , 过点O,且点E,H在边上,点G,F在边上,则阴影区域的面积与的面积比值是( )
3. 下列因式分解正确的是( )A、 B、 C、 D、4. 一个多边形的内角和与外角和相等,这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形5. 如图,的对角线 , 相交于点O, , 过点O,且点E,H在边上,点G,F在边上,则阴影区域的面积与的面积比值是( )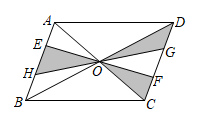 A、 B、 C、 D、6. 如图,是线段的垂直平分线,垂足为点G,E,F是上两点.下列结论错误的是( )
A、 B、 C、 D、6. 如图,是线段的垂直平分线,垂足为点G,E,F是上两点.下列结论错误的是( ) A、 B、 C、 D、7. 已知是完全平方式,则m的值是( )A、 B、 C、 D、8. 如图,在同一平面直角坐标系中,一次函数的图象与正比例函数的图象相交于点A,且点A的纵坐标是2,则不等式的解集是( )
A、 B、 C、 D、7. 已知是完全平方式,则m的值是( )A、 B、 C、 D、8. 如图,在同一平面直角坐标系中,一次函数的图象与正比例函数的图象相交于点A,且点A的纵坐标是2,则不等式的解集是( )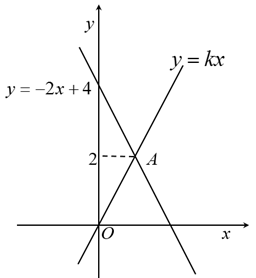 A、 B、 C、 D、9. 如图,在中, , , 以点C为圆心,长为半径作弧交于点D,分别以点A和点D为圆心,大于长为半径作弧,两弧相交于点E,作直线 , 交于点F,则的度数是( )
A、 B、 C、 D、9. 如图,在中, , , 以点C为圆心,长为半径作弧交于点D,分别以点A和点D为圆心,大于长为半径作弧,两弧相交于点E,作直线 , 交于点F,则的度数是( ) A、 B、 C、 D、10. 如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接 . 若 , , , 则的长是( )
A、 B、 C、 D、10. 如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接 . 若 , , , 则的长是( )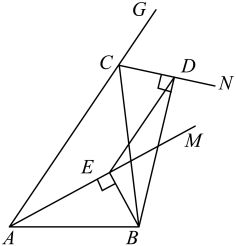 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 不等式的解集是 .12. 分解因式:3ax2+6axy+3ay2=.13. 若分式 有意义,则 的取值范围是 .14. 如图, , 是四边形的对角线,点E,F分别是 , 的中点,点M,N分别是 , 的中点,顺次连接 , , , , 若 , 则四边形的周长是 .
 15. 如图,一艘船从A处出发向正北航行50海里到达B处,分别从A,B望灯塔C,测得 , , 则B处到灯塔C的距离是海里.
15. 如图,一艘船从A处出发向正北航行50海里到达B处,分别从A,B望灯塔C,测得 , , 则B处到灯塔C的距离是海里. 16. 如图,在中, , , , 则的面积是 .
16. 如图,在中, , , , 则的面积是 .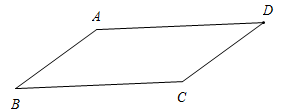 17. 如图,在中, , , , 点P为斜边上的一个动点(点P不与点A,B重合),过点P作 , , 垂足分别为点D和点E,连接 , 交于点Q,连接 , 当为直角三角形时,的长是 .
17. 如图,在中, , , , 点P为斜边上的一个动点(点P不与点A,B重合),过点P作 , , 垂足分别为点D和点E,连接 , 交于点Q,连接 , 当为直角三角形时,的长是 .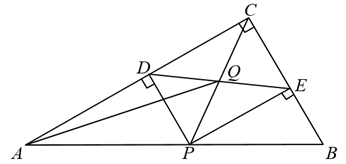 18. 如图,在中,对角线与相交于点 , 延长至点E,使得 , 连接交于点 , 连接 . 下列结论:①;②平分;③以点A,C,E,D为顶点构成的四边形是平行四边形;④ . 其中正确的是(填写所有正确结论的序号).
18. 如图,在中,对角线与相交于点 , 延长至点E,使得 , 连接交于点 , 连接 . 下列结论:①;②平分;③以点A,C,E,D为顶点构成的四边形是平行四边形;④ . 其中正确的是(填写所有正确结论的序号).
三、解答题
-
19. 先化简,再求值: , 再从0,1,2中选择一个合适的a值代入求值.20. 解不等式组: .21. 如图,点P,Q是对角线上的两个点,且 , 顺次连接 , , , .
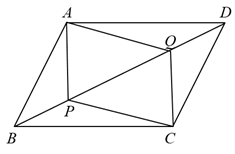
求证:四边形是平行四边形.
22. 在如图所示的平面直角坐标系中,每个小正方形的边长均为1,的三个顶点均在格点上,且 , , (本题不必写作图结论).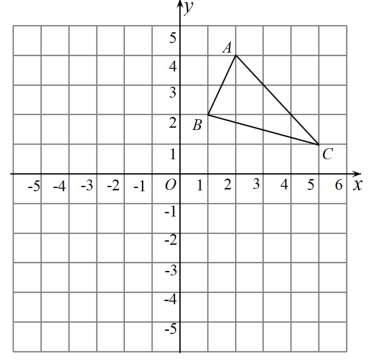
( 1 )将以点为旋转中心逆时针旋转 , 画出旋转后的 , 并直接写出点的坐标: ▲ , ▲ , ▲ ;
( 2 )画出向下平移6个单位长度后的 , 并直接写出点的坐标: ▲ , ▲ , ▲ ;
23. 某工厂安排A,B两种型号的机器加工同一种零件.已知一台A型机器比一台B型机器每天多加工10个这种零件,一台A型机器加工150个这种零件所用的时间与一台B型机器加工120个这种零件所用的时间相等.(1)、求A,B两种型号的机器每天各加工多少个这种零件?(2)、该工厂安排A,B两种型号的机器共20台同时加工这种零件,为确保每天完成不少于860个这种零件的加工任务,至少安排多少台A型号的机器?24. 在和中, , , , 连接 , , 是边上的中线.(1)、如图,当点D,E分别在边 , 延长线上时,请直接写出与的数量关系:;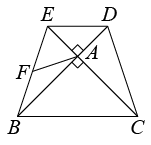 (2)、将绕点A旋转到如图的位置时,(1)中的结论是否成立?若成立,请完成证明;若不成立,写出你的结论并说明理由;
(2)、将绕点A旋转到如图的位置时,(1)中的结论是否成立?若成立,请完成证明;若不成立,写出你的结论并说明理由; (3)、若 , , 在绕点A旋转的过程中,当点C,D,E三点共线时,请直接写出线段的长.
(3)、若 , , 在绕点A旋转的过程中,当点C,D,E三点共线时,请直接写出线段的长.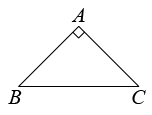 25. 如图,在平面直角坐标系中,的顶点O,B的坐标分别为 , , 将沿对角线翻折得到(点O,A,D在同一直线上),边与边相交于点E,此时,是等边三角形.
25. 如图,在平面直角坐标系中,的顶点O,B的坐标分别为 , , 将沿对角线翻折得到(点O,A,D在同一直线上),边与边相交于点E,此时,是等边三角形.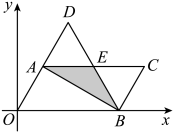 (1)、求线段的长;(2)、求重叠部分的面积;(3)、点N在轴上,点M在直线上,若以点B,C,M,N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
(1)、求线段的长;(2)、求重叠部分的面积;(3)、点N在轴上,点M在直线上,若以点B,C,M,N为顶点的四边形是平行四边形时,请直接写出点M的坐标.