江西省新余市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-29 类型:期末考试
一、单选题
-
1. 直线与y轴的交点坐标为( ).A、 B、 C、 D、2. 如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少走( )
 A、140米 B、120米 C、100米 D、90米3. 如图,已知菱形的对角线AC;BD交于点O,E为CD的中点,若 , 则菱形的周长为( ).
A、140米 B、120米 C、100米 D、90米3. 如图,已知菱形的对角线AC;BD交于点O,E为CD的中点,若 , 则菱形的周长为( ). A、18 B、48 C、24 D、124. 下列命题是假命题的是( )A、平行四边形的对角线互相平分 B、正方形的对角线相等且互相垂直平分 C、对角线相等的平行四边形是矩形 D、对角线互相垂直的四边形是菱形5. 如图,直线y=x+b与直线y=kx+6交于点P(1,3),则关于x的不等式x+b>kx+6的解集是( )
A、18 B、48 C、24 D、124. 下列命题是假命题的是( )A、平行四边形的对角线互相平分 B、正方形的对角线相等且互相垂直平分 C、对角线相等的平行四边形是矩形 D、对角线互相垂直的四边形是菱形5. 如图,直线y=x+b与直线y=kx+6交于点P(1,3),则关于x的不等式x+b>kx+6的解集是( ) A、 B、 C、 D、6. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间x(秒)之间的函数关系如图所示,则下列结论中正确的个数是( ).
A、 B、 C、 D、6. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间x(秒)之间的函数关系如图所示,则下列结论中正确的个数是( ).①乙的速度为5米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点60米;
③甲、乙两人之间的距离为40米时,甲出发的时间为55秒和90秒;
④乙到达终点时,甲距离终点还有80米.
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
7. 若代数式有意义,则实数x的取值范围是 .8. 现有甲、乙两种糖果的单价与千克数如下表所示:
甲种糖果
乙种糖果
单价(元/千克)
30
20
千克数
2
3
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为元/千克。
9. 当直线y=(1-k)x-3经过第二、三、四象限时,则k的取值范围是.10. 已知一组数据 , , , , 的平均数是3,则数据 , , , , 的平均数是 .11. 对实数a、b,定义“★”运算规则如下:a★b= , 则★(★)= .12. 如图,在矩形ABCD中, , , 点P从点A向点D以每秒1cm的速度运动,Q以每秒4cm的速度从点C出发,在B、C两点之间做往返运动,两点同时出发,点P到达点D为止(同时点Q也停止),这段时间内,当运动时间为时,P、Q、C、D四点组成矩形.
三、解答题
-
13. 计算:(1)、(2)、14. 如图,在中,点D在AB上,连接CD, , , , .
 (1)、求证:;(2)、求AC的长.15. 如图,在 ABCD中,E,F分别是AB,CD的中点,∠BFD=100°.求∠BED的大小.
(1)、求证:;(2)、求AC的长.15. 如图,在 ABCD中,E,F分别是AB,CD的中点,∠BFD=100°.求∠BED的大小. 16. 如图,点E是正方形外一点,且 . 请仅用无刻度的直尺按要求作图(保留作图痕迹).
16. 如图,点E是正方形外一点,且 . 请仅用无刻度的直尺按要求作图(保留作图痕迹). (1)、在图1中,作出BC边的中点M;(2)、在图2中,作出CD边的中点N.17. 如图,在四边形ABCD中, , 对角线BD垂直平分对角线AC;垂足为点O.求证:四边形是菱形.
(1)、在图1中,作出BC边的中点M;(2)、在图2中,作出CD边的中点N.17. 如图,在四边形ABCD中, , 对角线BD垂直平分对角线AC;垂足为点O.求证:四边形是菱形. 18. 每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共1200名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:
18. 每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共1200名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:七年级抽取的学生的竞赛成绩:
4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.

根据以上信息,解答下列问题:
(1)、填空:a= , b= , c=;(2)、根据以上数据分析,从中位数来看,年级成绩更优异;从合格率来看,年级成绩更优异;从方差来看,年级成绩更整齐;(3)、估计该校七、八年级共1200名学生中竞赛成绩达到9分及以上的约有多少人?19. 如图,一次函数y1=x+2的图象是直线l1 , 一次函数y2=kx+b的图象是直线l2 , 两条直线相交于点A(1,a),已知直线l1和l2与x轴的交点分别是点B,点C,且直线l2与y轴相交于点E(0,4).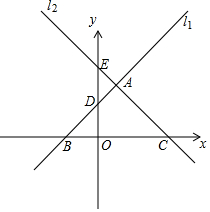 (1)、点A坐标为 , 点B坐标为 .(2)、求出直线l2的表达式;(3)、试求△ABC的面积.20. 从今年3月开始,上海的疫情时刻牵动着全国人民的心.4月9日,上海最大方舱医院投入使用,市政府计划派出360名医务工作者去上海方舱医院支援.经研究,决定租用当地租车公司提供的A,B两种型号客车共20辆作为交通工具,运送所有医务工作者去方舱医院.下表是租车公司提供的两种型号客车的载客量和租金信息。设租用A型号客车x辆,租车总费用为y元.
(1)、点A坐标为 , 点B坐标为 .(2)、求出直线l2的表达式;(3)、试求△ABC的面积.20. 从今年3月开始,上海的疫情时刻牵动着全国人民的心.4月9日,上海最大方舱医院投入使用,市政府计划派出360名医务工作者去上海方舱医院支援.经研究,决定租用当地租车公司提供的A,B两种型号客车共20辆作为交通工具,运送所有医务工作者去方舱医院.下表是租车公司提供的两种型号客车的载客量和租金信息。设租用A型号客车x辆,租车总费用为y元.型号
载客量
租金
A
20人/辆
300元/辆
B
15人/辆
240元/辆
(1)、求y关于x的函数解析式,并求出自变量x的取值范围;(2)、若要使租车总费用不超过5700元,一共有几种租车方案?并求出最低租车费用.21. 阅读下列解题过程:例:若代数式 , 求a的取值.
解:原式 ,
当时,原式 , 解得(舍去);
当时,原式 , 等式恒成立;
当时,原式 , 解得;
所以,a的取值范围是 .
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
(1)、当时,化简:;(2)、若 , 求a的取值;(3)、请直接写出满足的a的取值范围 .22. 如图1,在正方形中,点E是边CD上一点(点E不与点C、D重合),连接BE,过点A作交BC于点F.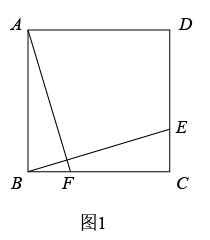

 (1)、求证:;(2)、如图2,取BE的中点M,过点M作 , 交AD于点G,交BC于点H.
(1)、求证:;(2)、如图2,取BE的中点M,过点M作 , 交AD于点G,交BC于点H.①求证:;
②连接CM,若 , 求GH的长;
(3)、如图3,取BE的中点M,连接CM,过点C作交AD于点G,连接EG、MG,若 , 则四边形的面积为 . (直接写出结果)23. 如图1,在平面直角坐标系中,点O是坐标原点,四边形是菱形,点A的坐标为 , 点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.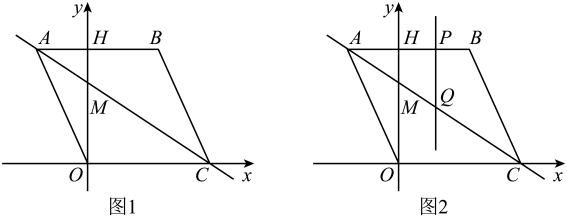 (1)、求菱形的边长;(2)、求直线AC的解析式:(3)、如图2,动点P从点A出发,沿折线向终点C运动,过点P作轴交AC于点Q,设点P的横坐标为a,线段PQ的长度为l.
(1)、求菱形的边长;(2)、求直线AC的解析式:(3)、如图2,动点P从点A出发,沿折线向终点C运动,过点P作轴交AC于点Q,设点P的横坐标为a,线段PQ的长度为l.①求l与a之间的函数关系式;
②取OM的中点N,请问以P、Q、N、M四点构成的四边形能否成为平行四边形?如果能成为平行四边形,请求出点P点Q的坐标,如果不能,请说明理由.