江西省南昌市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-29 类型:期末考试
一、单选题
-
1. 下列实数中,有理数是( )A、 B、 C、 D、2. 如图,菱形ABCD的周长是4cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
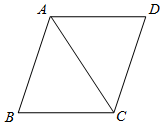 A、1cm B、2 cm C、3cm D、4cm3. 在平面直角坐标系中,函数的图象如图所示,则下列判断正确的是( )
A、1cm B、2 cm C、3cm D、4cm3. 在平面直角坐标系中,函数的图象如图所示,则下列判断正确的是( ) A、 B、 C、 D、4. 一个四边形顺次添加下列中的三个条件便得到正方形:
A、 B、 C、 D、4. 一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( )
A、仅① B、仅③ C、①② D、②③5. 从一组数据中取出a个x1 , b个x2 , c个x3 , 组成一个样本,那么这个样本的平均数是( )A、 B、 C、 D、6. 如图,直线 经过点 ,则不等式 的解集为( )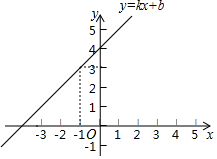 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 在平面直角坐标系中,若一次函数的图象过点 , , 则m的值为 .8. 如图所示,在正方形ABCD中,点P在AC上, , ,垂足分别为E,F, ,则DP的长为 .
 9. 若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .10. “共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩, , 则品种更适合在该村推广.(填“甲”或“乙”)11. 如图,在矩形 中, 是 边上一点, 是 边的中点, ,则 .
9. 若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .10. “共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩, , 则品种更适合在该村推广.(填“甲”或“乙”)11. 如图,在矩形 中, 是 边上一点, 是 边的中点, ,则 .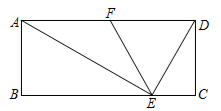 12. 已知a,b,c分别是的三条边长,c为斜边长, , 我们把关于x的形如的一次函数称为“勾股一次函数”.若点在“勾股一次函数”的图象上,且的面积是4,则c的值是 .
12. 已知a,b,c分别是的三条边长,c为斜边长, , 我们把关于x的形如的一次函数称为“勾股一次函数”.若点在“勾股一次函数”的图象上,且的面积是4,则c的值是 .三、解答题
-
13. 化简(1)、(2)、14. 只用无刻度的直尺作图(保留作图痕迹,不要求写作法).
如图,已知 , , 点E在OB边上,其中四边形AEBF是平行四边形,

 (1)、请在图中画出的平分线.(2)、请在图中画出菱形AOBN.15. 已知:中, , , BC边上的高 , 求BC.16. 如图,将两张长为10,宽为4的矩形纸条交叉叠放,使一组对角的顶点重合,其重叠部分是四边形AGCH.
(1)、请在图中画出的平分线.(2)、请在图中画出菱形AOBN.15. 已知:中, , , BC边上的高 , 求BC.16. 如图,将两张长为10,宽为4的矩形纸条交叉叠放,使一组对角的顶点重合,其重叠部分是四边形AGCH. (1)、证明:四边形AGCH是菱形;(2)、求菱形AGCH的周长.17. 如图,直线的函数表达式为: , 与x轴交于点B,直线经过点 , 并与直线交于点 .
(1)、证明:四边形AGCH是菱形;(2)、求菱形AGCH的周长.17. 如图,直线的函数表达式为: , 与x轴交于点B,直线经过点 , 并与直线交于点 .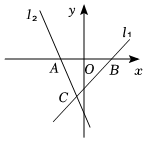 (1)、求直线的解析式;(2)、点P在直线上,点Q在直线上,轴,若 , 求点P的坐标.18. 2022年北京冬奥会和冬残奥会的吉祥物冰墩墩和雪容融深受国内外广大朋友的喜爱,北京奥组委会官方也推出了许多吉祥物的周边产品.现有以下两款:
(1)、求直线的解析式;(2)、点P在直线上,点Q在直线上,轴,若 , 求点P的坐标.18. 2022年北京冬奥会和冬残奥会的吉祥物冰墩墩和雪容融深受国内外广大朋友的喜爱,北京奥组委会官方也推出了许多吉祥物的周边产品.现有以下两款:已知购买3个冰墩墩和2个雪容融需要560元;购买1个冰墩墩和3个雪容融需要420元:
 (1)、请问冰墩墩和雪容融每个的售价分别是多少元?(2)、北京奥运官方特许零售店开始销售的第一天4个小时内全部售罄,于是从厂家紧急调配24000个商品,拟租用甲、乙两种车共6辆,一次性将商品送到指定地点,若每辆甲种车的租金为400元可装载4500个商品,每辆乙种车的租金为280元可装载3000个商品,请给出最节省费用的租车方案,并求出最低费用.19. 学校组织七、八年级全体学生开展了“防诈骗”网上竞赛活动.为了解竞赛情况,从两个年级各随机抽取了10名同学的成绩(满分为100分).收集数据:七年级:90,95,95,80,90,80,85,90,85,100;八年级:85,85,95,80,95,90,90,90,100,90.
(1)、请问冰墩墩和雪容融每个的售价分别是多少元?(2)、北京奥运官方特许零售店开始销售的第一天4个小时内全部售罄,于是从厂家紧急调配24000个商品,拟租用甲、乙两种车共6辆,一次性将商品送到指定地点,若每辆甲种车的租金为400元可装载4500个商品,每辆乙种车的租金为280元可装载3000个商品,请给出最节省费用的租车方案,并求出最低费用.19. 学校组织七、八年级全体学生开展了“防诈骗”网上竞赛活动.为了解竞赛情况,从两个年级各随机抽取了10名同学的成绩(满分为100分).收集数据:七年级:90,95,95,80,90,80,85,90,85,100;八年级:85,85,95,80,95,90,90,90,100,90.整理数据:
分数
80
85
90
95
100
七年级
2
2
3
2
1
八年级
1
2
4
a
1
分析数据:
平均数
中位数
众数
方差
七年级
89
b
90
39
八年级
c
90
d
30
根据以上信息回答下列问题:
(1)、请直接写出表格中a,b,c,d的值;(2)、通过数据分析,你认为哪个年级的成绩比较好?请说明理由;(3)、该校七、八年级共有600人,本次竞赛成绩不低于90分的为“优秀”.估计这两个年级共有多少名学生达到“优秀”?四、八年级成绩的众数和中位数相同,但是八年级的平均成绩比七年级的高,且从方差看,八年级的方差更小,成绩更稳定,
-
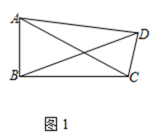
20. 定义:有一个内角为90°,且对角线相等的四边形称为准矩形.(1)、如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=4,则BD=;
 (2)、如图2,正方形ABCD中,点E,F分别是边AD,AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(2)、如图2,正方形ABCD中,点E,F分别是边AD,AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;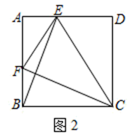 (3)、如图3,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,AC=DC,求这个准矩形的面积.
(3)、如图3,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,AC=DC,求这个准矩形的面积.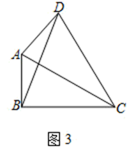 21. 学习一次函数时,我们通过列表、描点、连线画出一次函数图象,并结合函数图象研究函数性质。小南结合学习一次函数的经验,对函数的图像和性质进行了研究,下面是小南的探讨过程,请补充完整:(1)、列表:
21. 学习一次函数时,我们通过列表、描点、连线画出一次函数图象,并结合函数图象研究函数性质。小南结合学习一次函数的经验,对函数的图像和性质进行了研究,下面是小南的探讨过程,请补充完整:(1)、列表:x
…
-2
-1
0
1
2
3
…
y
…
m
1
2
3
2
n
…
表格中 , ;
(2)、
①根据列表在给出的平面直角坐标系中描点、画出函数图象;
②根据所画的函数图象,该函数有(填“最大值”或“最小值”);这个值为;
(3)、直接写出函数图象与x轴所围成的图形的面积:;(4)、过点作直线l//x轴,结合所画的函数图象,若直线l与函数图像有两个交点,请直接写出a的取值范围.