江西省抚州市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 一次函数y=（m﹣3）x+m+2的图象经过第一、二、四象限，则m的取值范围在数轴上表示为（　　）

A、 B、 C、 D、

查看试题解析
3. 一个多边形的内角和是外角和的3倍，则这个多边形的边数是（　　）

A、4 B、8 C、10 D、12

查看试题解析
4. 如图，已知AB＝AC＝7，BC＝5，以A，B两点为圆心，大于 $\frac{1}{2}$ AB的长为半径画圆弧，两弧相交于点M，N，连接MN与AC相交于点D，则△BCD的周长是（　　）

A、12 B、14 C、15 D、17

查看试题解析
5. 如图，点A，B，C在一条直线上，△ABD和△BCE是等边三角形，连接AE和CD交于点M，则∠AMC的度数为（　　）

A、135° B、120° C、105° D、90°

查看试题解析
6. 如图，在平行四边形ABCD中，对角线AC，BD交于点O，BD＝2AD，E，F，G分别是OA，OB，CD的中点，EG交FD于点H．则下列结论：①ED⊥CA；②EF＝CG；③EH= $\frac{1}{2}$ EG；④S_△EFD＝S_△CEG成立的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 分解因式：3m²﹣3n²＝．

查看试题解析
8. 已知分式 $\frac{(x + 2021) (x - 2022)}{x + 2021}$ 的值为0，则x的值为．

查看试题解析
9. 若分式方程有 $\frac{2}{x - 1} + 3 = \frac{m}{x - 1}$ 增根，则m的值是．

查看试题解析
10. 如图，在△ABC中，∠C＝90°，∠A＝15°，∠DBC＝60°，BC＝ $\sqrt{3}$ ，则AD的长为．

查看试题解析
11. 如图，等腰△ABC的底边BC＝20，面积为160，点F是BC边上的一个动点，EG是腰AC的垂直平分线，若点D在EG上运动，则CD+DF的最小值为．

查看试题解析
12. 如图所示，在平行四边形ABCD中，AB＝5cm，AD＝9cm．点P在AD边上以1cm/s的速度从点A向点D运动，点Q在BC边上以4cm/s的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时，P、Q同时停止运动，设运动时间为t（s）且t＞0，当以P，D，Q，B为顶点的四边形是平行四边形时，则t的所有可能值为．

查看试题解析

三、解答题

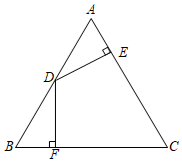
13. 计算

(1)、解不等式组： ${\begin{array}{l} 2 (x + 3) \leq 4 x + 7 \\ \frac{x + 2}{2} > x \end{array}$ ；

(2)、解方程： $\frac{x}{x - 1} - 1 = \frac{3}{x^{2} - 1}$ ．

查看试题解析
14. 如图，在△ABC中，AB＝AC，D为AB边的中点，DE⊥AC于点E，DF⊥BC于点F，DE＝DF．求证：△ABC是等边三角形．

查看试题解析
15. 已知 $\frac{1}{b} - \frac{1}{a}$ ＝5，求 $\frac{3 a + 2 a b - 3 b}{a - a b - b}$ 的值．

查看试题解析
16. 如图所示：

(1)、在图①中画出△ABC先向上平移3个单位，再向右平移2个单位后得到的图形．

(2)、在图②中画出△ABC绕点C逆时针旋转90°后得到的图形．

查看试题解析
17. 已知x为整数，且 $\frac{2}{x + 3}$ + $\frac{2}{3 - x}$ + $\frac{2 x + 18}{x^{2} - 9}$ 化简结果为整数，求出所有符合条件的x值．

查看试题解析
18. 如图，点O是△ABC内一点，连接OB，OC，并将AB，OB，OC，AC的中点D，E，F，G依次连接，得到四边形DEFG．

(1)、求证：四边形DEFG是平行四边形．

(2)、如果∠OBC＝45°，∠OCB＝30°，OC＝8，求EF的长．

查看试题解析
19. 在今年新冠肺炎防疫工作中，某公司购买了A、B两种不同型号的口罩，已知A型口罩的单价比B型口罩的单价多1.5元，且用8800元购买A型口罩的数量与用5500元购买B型口罩的数量相同．

(1)、A、B两种型号口罩的单价各是多少元？

(2)、根据疫情发展情况，该公司还需要增加购买一些口罩，增加购买B型口罩的数量是A型口罩数量的2倍，若总费用不超过3600元，则增加购买A型口罩的数量最多是多少个？

查看试题解析
20. 在理解例题的基础上，完成下列两个问题：
例题：若m²+2mn+2n²﹣4n+4＝0，求m和n的值；
解：由题意得：（m²+2mn+n²）+（n²﹣4n+4）＝0，
∴（m+n）²+（n﹣2）²＝0
∴ ${\begin{array}{l} m + n = 0 \\ n - 2 = 0 \end{array}$ ，解得 ${\begin{array}{l} m = - 2 \\ n = 2 \end{array}$ ．请解决以下问题：

(1)、若x²+4xy+5y²﹣4y+4＝0，求yx的值；

(2)、若a，b，c是△ABC的边长，满足a²+b²＝12a+8b﹣52，c是△ABC的最长边，且c为偶数，则c可能是哪几个数？

查看试题解析
21. 如图1，在平行四边形ABCD中，过点A作AE⊥BC交BC于点E，连接ED，且ED平分∠AEC．

(1)、求证：AE＝BC；

(2)、如图2，过点C作CF⊥DE交DE于点F，连接AF，BF，猜想△ABF的形状并证明．

查看试题解析
22. 定义运算min{a，b}，当a≥b时，min{a，b}＝b；当a＜b时，min{a，b}＝a；如：min{4，0}＝0；min{2，2}＝2；min{﹣3，﹣1}＝﹣3．根据该定义运算完成下列问题：

(1)、min{﹣3，2}＝，当x≤2时，min{x，2}＝；

(2)、如图，已知直线y₁＝x+m与y₂＝kx﹣2相交于点P（﹣2，1），若min{x+m，kx﹣2）＝kx﹣2，结合图象，直接写出x的取值范围是．

(3)、在（2）的基础上，直线y₁＝x+m交x轴于点C，交y轴于点A，直线y₂＝kx﹣2交x轴于点B，求△ABP的面积．

查看试题解析
23.

(1)、阅读理解：如图①，在四边形ABCD中，AB $∥$ CD，点E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，CD之间的等量关系．
解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC，得到AB＝CF，从而把AB，AD，CD转化在一个三角形中即可判断：AB，AD，CD之间的等量关系为；

(2)、问题探究：如图②，在四边形ABCD中，AB $∥$ CD，AF与DC的延长线交于点F，点E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论；

(3)、问题解决：如图③，AB $∥$ CF，AE与BC交于点E，且点E是BC的中点，点D在线段AE上，且∠EDF＝∠BAE＝30°，若AB＝6，CF＝2，求CD的值．

查看试题解析