吉林省长春市长春新区2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2022-08-29 类型:期末考试
一、单选题
-
1. 下列代数式中,属于分式的是( )A、 B、 C、 D、2. “”表示此类型的口罩能过滤空气中的粒径约为的非油性颗粒,其中用科学记数法表示为( ).A、 B、 C、 D、3. 在平面直角坐标系中,点P的坐标为 , 那么点P在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 把分式中的x,y的值同时扩大为原来的2倍,则分式的值( )A、不变 B、扩大为原来的2倍 C、扩大为原来的4倍 D、缩小为原来的5. 如图,在四边形ABCD中,ABCD,要使四边形ABCD是平行四边形,下列添加的条件错误的是( )
 A、AB=CD B、BC=AD C、∠A=∠C D、6. 某同学这学期前四次数学测验的成绩依次为93、82、76和88,马上要进行第五次数学测验了,她这五次成绩的平均数能够达到或超过85分,那么,这次测验她的分数至少是( )A、83 B、84 C、85 D、867. 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处,易证四边形AECF是平行四边形.当∠BAE为( )度时,四边形AECF是菱形.
A、AB=CD B、BC=AD C、∠A=∠C D、6. 某同学这学期前四次数学测验的成绩依次为93、82、76和88,马上要进行第五次数学测验了,她这五次成绩的平均数能够达到或超过85分,那么,这次测验她的分数至少是( )A、83 B、84 C、85 D、867. 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处,易证四边形AECF是平行四边形.当∠BAE为( )度时,四边形AECF是菱形. A、30° B、40° C、45° D、50°8. 在同一直角坐标系中,函数 与 的图象可能是( )A、
A、30° B、40° C、45° D、50°8. 在同一直角坐标系中,函数 与 的图象可能是( )A、 B、
B、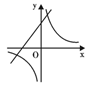 C、
C、 D、
D、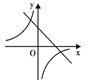
二、填空题
-
9. 计算: .10. 当式子有意义时,实数的取值范围是 .11. 在平面直角坐标系中,将直线沿着y轴向下平移3个单位长度,平移后的直线所对应的函数解析式为 .12. 在平面直角坐标系中,一次函数y=kx和y=-x+3的图象如图所示,则二元一次方程组的解是 .
 13. 如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2 .
13. 如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2 .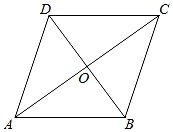 14. 在平面直角坐标系中,若点、、都在函数的图象上,则、、的大小关系是(用“>”号连接).
14. 在平面直角坐标系中,若点、、都在函数的图象上,则、、的大小关系是(用“>”号连接).三、解答题
-
15. 先化简,再求值: , 其中 .16. 为丰富师生的体育文化生活,某中学决定组建足球社团,学校在商场购进A、B两种品牌的足球,购买A品牌足球花费了2000元,购买B品牌足球花费了2500元,且购买A品牌足球数量是购买B品牌足球数量的2倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元,问购买一个B品牌的足球花费多少钱?17. 图①、图②都是4×4的正方形网格,每个小正方形的顶点称为格点,点A、B均在格点上,仅用无刻度的直尺在下列网格中按要求作图.
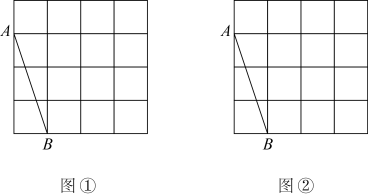 (1)、在图①中,画出一个以AB为边的四边形ABCD,使其是中心对称图形不是轴对称图形且边长均为无理数.(2)、在图②中,画出一个以线段AB为边的四边形ABMN,使其既是轴对称图形又是中心对称图形.18. 如图,在△ABC中,AB=AC,AD⊥BC于点D,过点B作AD的平行线交外角∠BAF的平分线于点E.求证:四边形ADBE是矩形.
(1)、在图①中,画出一个以AB为边的四边形ABCD,使其是中心对称图形不是轴对称图形且边长均为无理数.(2)、在图②中,画出一个以线段AB为边的四边形ABMN,使其既是轴对称图形又是中心对称图形.18. 如图,在△ABC中,AB=AC,AD⊥BC于点D,过点B作AD的平行线交外角∠BAF的平分线于点E.求证:四边形ADBE是矩形. 19. 如图,在平面直角坐标系中,O为坐标原点,点A,B在函数的图象上(点A的纵坐标大于点B的纵坐标),点A的坐标为(2,4),过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连结OA,AB.
19. 如图,在平面直角坐标系中,O为坐标原点,点A,B在函数的图象上(点A的纵坐标大于点B的纵坐标),点A的坐标为(2,4),过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连结OA,AB. (1)、求k的值.(2)、若CD=2OD,求四边形OABC的面积.20. 某校为了调查学生对环境保护知识的了解情况,从七、八两个年级各随机抽取50名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析,下面给出了部分信息:
(1)、求k的值.(2)、若CD=2OD,求四边形OABC的面积.20. 某校为了调查学生对环境保护知识的了解情况,从七、八两个年级各随机抽取50名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析,下面给出了部分信息:a.八年级50名学生成绩的频数分布统计表如下:
成绩x
学生人数
5
14
15
13
3
b.八年级成绩在这一组的是:
71 71 72 72 73 75 75 75 76 77 77 78 79 79 79
c.七、八两个年级成绩的平均分、中位数、众数和方差如下.
年级
平均数
中位数
方差
七
74
73.8
122.3
八
74
n
89.2
根据以上信息,回答下列问题:
(1)、表格中n= .(2)、在此次测试中,某学生的成绩是74.5分,在他所属年级排在前20名,由表中数据可知该学生是年级的学生.(填“七”或“八”)(3)、根据以上信息,你认为七、八两个年级中,哪个年级学生了解环境保护知识的情况较好,请从两个方面说出你的判断依据.21. 小明和小红分别从甲、乙两地沿同一条路同时出发,相向而行.小明从甲地到乙地,小红从乙地到甲地,小明和小红离甲地的距离y(千米)与时间x(小时)之间的函数图象如图所示,根据图中提供的信息,解答下列问题: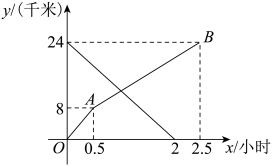 (1)、小红出发后速度为千米/小时.(2)、求线段AB对应的函数表达式,写出自变量x的取值范围.(3)、当小红到达甲地时,小明距乙地还有多远?22. 【阅读材料】如图①,在边长为4的正方形ABCD中,点E、F分别在边BC、CD上且∠EAF=45°,连接EF,求△CEF的周长.
(1)、小红出发后速度为千米/小时.(2)、求线段AB对应的函数表达式,写出自变量x的取值范围.(3)、当小红到达甲地时,小明距乙地还有多远?22. 【阅读材料】如图①,在边长为4的正方形ABCD中,点E、F分别在边BC、CD上且∠EAF=45°,连接EF,求△CEF的周长.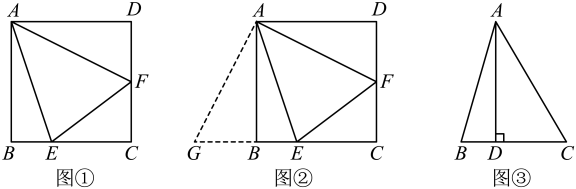
小明想到解决问题的方法如下:
如图②,延长CB至点G,使BG=DF,通过证明 , 得到BE、DF、EF之间的关系,进而求出△CEF的周长.
(1)、请按照小明的思路,帮助小明写出完整的求解过程.(2)、【方法应用】如图②,若BE=1,求DF的长.(3)、【能力提升】如图③,在锐角△ABC中,∠BAC=45°,AD⊥BC于点D.若BD=1,AD=4,则CD的长为 .23. 如图,在中,AB=5,BC=9,的面积为36,动点P从A点出发,以1个单位长度的速度沿线段AD向终点D运动,同时动点Q从点B出发以3个单位长度的速度在BC间往返运动,当点P到达点D时,动点P、Q同时停止运动,连结PQ.设运动时间为t秒. (1)、直线AD与BC之间的距离是 .(2)、当点Q从点C向点B运动时(点Q不与点B、C重合),设四边形ABQP的面积为S,求S与t之间的函数关系式,并写出自变量t的取值范围.(3)、当PQ⊥BC时,求t的值.(4)、当PQ平分的面积时,直接写出t的值.24. 在平面直角坐标系中,函数的图象记作G(其中m为常数,且m≠0),点M坐标为 , 点N坐标为(3,1).
(1)、直线AD与BC之间的距离是 .(2)、当点Q从点C向点B运动时(点Q不与点B、C重合),设四边形ABQP的面积为S,求S与t之间的函数关系式,并写出自变量t的取值范围.(3)、当PQ⊥BC时,求t的值.(4)、当PQ平分的面积时,直接写出t的值.24. 在平面直角坐标系中,函数的图象记作G(其中m为常数,且m≠0),点M坐标为 , 点N坐标为(3,1). (1)、当图象过点N时,求m的值.(2)、在(1)的条件下.
(1)、当图象过点N时,求m的值.(2)、在(1)的条件下.①在给定的平面直角坐标系内画出图象G.
②当时,求函数值y的最大值和最小值.
(3)、当图象G与线段MN只有一个交点时,直接写出m的取值范围.