吉林省白城市洮北区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是（）

A、x≤3 B、x＜3 C、x≥3 D、x＞3

查看试题解析
2. 下列根式中，不是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{10}$ C、 $\sqrt{6}$ D、 $\sqrt{2}$

查看试题解析
3. 若y=x+2–b是正比例函数，则b的值是（）

A、0 B、–2 C、2 D、–0.5

查看试题解析
4. 学校准备从甲、乙、丙、丁四个科技创新小组中选出一组代表学校参加青少年科技创新大赛，各组的平时成绩的平均数 $\bar{x}$ （单位：分）及方差 $s^{2}$ 如表所示：

甲

乙

丙

丁

$\bar{x}$

7

8

8

7

$s^{2}$

1

1.2

1

1.8

如果要选出一个成绩较好且状态稳定的组去参赛，那么应选的组是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 已知点 $A (2 ， m)$ ， $B (- 1 ， n)$ 在一次函数 $y = 2 x + 1$ 的图象上，则m与n的大小关系是（）

A、 $m > n$ B、m=n C、m＜n D、无法确定

查看试题解析
6. 如图，AB∥DC，ED∥BC，AE∥BD，那么图中和△ABD面积相等的三角形（不包括△ABD）有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 计算： $\sqrt{3} \div \sqrt{6}$ =

查看试题解析
8. 任意四边形的中点四边形是形．

查看试题解析
9. 请你写出一个图像不经过第三象限的一次函数解析式．

查看试题解析
10. 如图，在菱形 $A B C D$ 中， $A C$ 与 $B D$ 交于点O，若 $A C ＝ 8 ， B D ＝ 6$ ，则菱形 $A B C D$ 的面积为．

查看试题解析
11. 直线 $y = 2 x - 1$ 与直线 $y = (k - 1) x + 2$ 平行，则k＝．

查看试题解析
12. 如图，正方形ODBC中，OC=1，OA=OB，则数轴上点A表示的数是．

查看试题解析
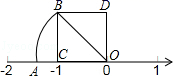13. 如图，在Rt△ABC中，∠ABC＝90°，∠C＝60°，点D为边AC的中点，BD＝2，则BC的长为．

查看试题解析
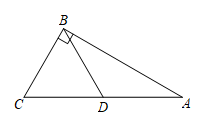14. 甲和乙同时加工一种产品，他们的工作量与工作时间的关系如图所示，则当甲加工了这种产品70件时，乙加工了件.

查看试题解析

三、解答题

15. 计算： $\sqrt{12} + 4 \sqrt{0.5} - \frac{2}{3} \sqrt{18} + 3 \sqrt{\frac{1}{3}}$ ．

查看试题解析
16. 已知 $x = 2 + \sqrt{3}$ ， $y = 2 - \sqrt{3}$ ，求代数式 $x^{2} + 2 x y + y^{2}$ 的值．

查看试题解析
17. 如图，每个小正方形的边长都为1．

(1)、求 $△ A B C$ 的周长．

(2)、求 $∠ A B C$ 的大小．

查看试题解析
18. 等腰三角形的周长是16，求出底边长y与一腰长x的函数关系式，并求出自变量x的取值范围？

查看试题解析
19. 如图，在▱ABCD中，E为BC边上一点，且AB＝AE.

(1)、求证：△ABC≌△EAD；

(2)、若∠B＝65°，∠EAC＝25°，求∠AED的度数.

查看试题解析
20. 如图，小颖和她的同学荡秋千，秋千AB在静止位置时，下端B离地面0.6m，荡秋千到AB的位置时，下端B距静止位置的水平距离EB等于2.4m，距地面1.4m，求秋千AB的长.

查看试题解析
21. 某中学为了解初三学生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下：3；5；3；6；3；4；4；5；2；4；5；6；1；3；5；5；4；4；2；4
根据以上数据，得到如下不完整的频数分布表：

次数

1

2

3

4

5

6

人数

1

2

a

6

b

2

(1)、表格中的 $a =$ ， $b =$ ；

(2)、在这次调查中，参加志愿者活动的次数的众数为，中位数为；

(3)、若该校初三年级共有300名学生，根据调查统计结果，估计该校初三年级学生参加志愿者活动的次数为4次的人数．

查看试题解析
22. 如图，四边形ABCD是一个正方形花园，E、F是它的两个门，且 $D E = C F$ ，要修建两条路BE和AF，这两条路等长吗？它们有什么位置关系？请证明你的猜想．

查看试题解析
23. 为了做好防疫工作，学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元，5瓶A型消毒液和2瓶B型消毒液共需53元.

(1)、这两种消毒液的单价各是多少元？

(2)、学校准备购进这两种消毒液共90瓶，且B型消毒液的数量不少于A型消毒液数量的 $\frac{1}{3}$ ，请设计出最省钱的购买方案，并求出最少费用.

查看试题解析
24. 如图，直线 $l_{1}$ 的解析表达式为： $y = - 3 x + 3$ ，且直线 $l_{1}$ 与x轴交于点D，直线 $l_{2}$ 经过点A（4，0）， $B (3 ， - \frac{3}{2})$ ，直线 $l_{1}$ ， $l_{2}$ 交于点C．

(1)、求点D的坐标；

(2)、求直线 $l_{2}$ 的解析表达式；

(3)、求△ADC的面积；

(4)、在直线 $l_{2}$ 上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．

查看试题解析
25. 如图①，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．

(1)、求证：△BDF是等腰三角形．

(2)、如图②，过点D作DG//BE，交BC于点G，连接FG交BD于点O．
①判断四边形BFDG的形状，并说明理由；
②若AB＝6，AD＝8，求FG的长．

查看试题解析
26. A，B，C三地在同一条公路上，C地在A，B两地之间，且到A，B两地的路程相等，甲、乙两车同时分别从A，B两地出发，匀速行驶，甲车到达C地并停留1小时后以原速继续前往B地，到达B地后立即调头（调头时间忽略不计），并按原路原速返回C地停止行驶，乙车经C地到达A地停止行驶．在两车行驶的过程中，甲、乙两车距C地的路程y（单位：千米）与所用的时间x（单位：小时）之间的函数图象如图所示，请结合图象信息解答下列问题：

(1)、直接写出A，B两地的路程和甲车的速度；

(2)、求乙车从C地到A地的过程中y与x的函数关系式，并写出自变量x的取值范围；

(3)、出发后几小时，两车在途中距C地的路程之和为180千米？请直接写出答案．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	7	8	8	7
$s^{2}$	1	1.2	1	1.8

次数	1	2	3	4	5	6
人数	1	2	a	6	b	2