黑龙江省牡丹江市宁安市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-29 类型：期末考试

进入出卷网下载

一、单选题

1. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥－2 B、x>－2 C、x≥2 D、x<2

查看试题解析
2. 以下二次根式：① $\sqrt{12}$ ；② $\sqrt{2^{2}}$ ；③ $\sqrt{\frac{2}{3}}$ ；④ $\sqrt{27}$ 中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、①和② B、②和③ C、①和④ D、③和④

查看试题解析
3. 数据0，1，2，3，x的平均数是2，则这组数据的方差是（）

A、2 B、 $\sqrt{2}$ C、10 D、 $\sqrt{10}$

查看试题解析
4. 下列命题中，真命题是（　　）

A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形

查看试题解析
5. 下列图像中，y不是 x的函数的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE＝DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）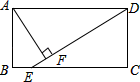

A、△AFD≌△DCE B、AF＝ $\frac{1}{2}$ AD C、AB＝AF D、BE＝AD﹣DF

查看试题解析
7. 如图，在长方形 $A B C D$ 中无重叠放入面积分别为 $16 c m^{2}$ 和 $12 c m^{2}$ 的两张正方形纸片，则图中空白部分的面积为（） $c m^{2}$

A、 $16 - 8 \sqrt{3}$ B、 $- 12 + 8 \sqrt{3}$ C、 $8 - 4 \sqrt{3}$ D、 $4 - 2 \sqrt{3}$

查看试题解析
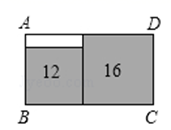8. 如图，▱ABCD中，EF过对角线的交点O ， AB=4，AD=3，OF=1.3，则四边形BCEF的周长为（）

A、8.3 B、9.6 C、12.6 D、13.6

查看试题解析
9. 如果直线 $y = 3 x + 6$ 与 $y = 2 x - 4$ 交点坐标是（a，b），则 ${\begin{array}{l} x = a \\ y = b \end{array}$ 是下面哪个方程组的解（）

A、 ${\begin{array}{l} y - 3 x = 6 \\ 2 y + x = - 4 \end{array}$ B、 ${\begin{array}{l} y - 3 x = 6 \\ 2 y - x = - 4 \end{array}$ C、 ${\begin{array}{l} 3 x - y = 6 \\ 3 x - y = 4 \end{array}$ D、 ${\begin{array}{l} 3 x - y = - 6 \\ 2 x - y = 4 \end{array}$

查看试题解析
10. 如图，函数 $y = 2 x$ 和 $y = a x + 4$ 的图象相交于点 $A (m ， 3)$ ，则不等式 $2 x \geq a x + 4$ 的解集为（）

A、 $x \leq 3$ B、 $x \geq \frac{3}{2}$ C、 $x \geq 3$ D、 $x \leq \frac{3}{2}$

查看试题解析
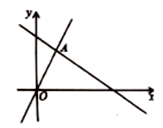11. 如图，在菱形ABCD中，M，N分别在AB，CD上，且AM＝CN，MN与AC交于点O，连接BO．若∠DAC＝28°，则∠OBC的度数为（　　）

A、28° B、52° C、62° D、72°

查看试题解析
12. 如图，边长为4的正方形ABCD中，点E，F分别是边BC，DC上的点，且∠EAF=45°，下列结论：① $S_{Δ A B E} + S_{Δ A D F} = S_{Δ A E F}$ ；②BE+DF=EF；③当△ABE≌△ADF时，EF的长为 $8 \sqrt{2} - 8$ ；④当EF=4时，△CEF是等腰直角三角形，其中正确结论的个数是（）

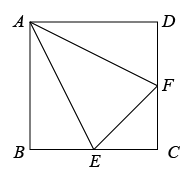A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 计算： $(\sqrt{3} - 2)^{2021} \cdot (\sqrt{3} + 2)^{2022} =$ ．

查看试题解析
14. 一组数据2，6，8，10，x的众数是6，则这组数据的中位数是．

查看试题解析
15. 如图，要使平行四边形ABCD为菱形，还需添加的一个条件是．（写出一个即可）．

查看试题解析
16. 如图，将长8cm，宽4cm的矩形ABCD纸片折叠，使点A与C重合，则折痕EF的长为cm．

查看试题解析
17.
如图，已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm，AE⊥BC于点E，则AE的长是．

查看试题解析
18. 如图，由等圆组成的一组图中，第1个图由1个圆组成，第2个图由5个圆组成，第3个图由11个圆组成，…，按照这样的规律排列下去，则第9个图形由个圆组成，

查看试题解析
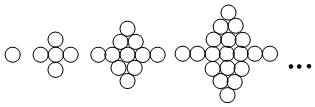19. 已知矩形ABCD中，BE平分∠ABC交矩形的一条边于点E，若BD＝10，∠EBD＝15°，则AB＝．

查看试题解析
20. 关于函数 $y = - x - 2$ 的图象，有如下说法：①图象过点 $(0 ， - 2)$ ；②图象与x轴的交点的坐标为 $(- 2 ， 0)$ ；③y随x的增大而增大；④图象不经过第一象限；⑤图象是与直线 $y = - x + 2$ 平行的直线．其中正确的是（填序号）

查看试题解析

三、解答题

21. 计算 $(7 + 4 \sqrt{3}) (7 - 4 \sqrt{3}) - (2 \sqrt{5} - 1)^{2}$

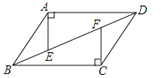
查看试题解析
22.
如图，四边形ABCD中，AD∥BC，AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE=CF．求证：四边形ABCD是平行四边形．

查看试题解析
23. 某厂为了解工人在单价时间内加工同一种零件的技能水平，随机抽取了50名工人加工的零件进行检测，统计出他们各自加工的合格品数是1到8这八个整数，现提供统计图的部分信息如图，
请解答下列问题：

(1)、根据统计图，求这50名工人加工出的合格品数的中位数．

(2)、写出这50名工人加工出合格品数的众数的可能取值

(3)、厂方认定，工人在单位时间内加工出的合格品数不低于3件为技能合格，否则，将接受技能再培训．已知该厂有同类工人400名，请估计该厂将接受技能再培训的人数．

查看试题解析
24. 在△ABC中，∠C=90°，∠A=30°，BC=2，以AB为边作等边△ABD，点E为线段AD的中点，连接CE，请画出图形，并直接写出线段CE的长．

查看试题解析
25. 快、慢两车分别从相距360km的甲、乙两地出发，匀速行驶，先相向而行，慢车在快车出发1h后出发，到达甲地后停止行驶，快车到达乙地后，立即按原路原速返回甲地（快车调头的时间忽略不计），快、慢两车距乙地的路程y（km）与快车出发时间x（h）之间的函数图象如图所示，请结合图象信息解答下列问题：

(1)、直接写出慢车的行驶速度，并直接在图中的（）内填上正确的数；

(2)、求图象中BC所在直线的函数解析式；

(3)、请直接写出快车出发后几小时与慢车第一次相遇？此时距离甲地的路程是多少千米？

查看试题解析
26. AM∥BN，AB $⊥$ BN，垂足为B，点C在直线BN上，AC $⊥$ CD，AC=CD，DE $⊥$ AM，垂足为E．

(1)、如图①，求证：DE+BC=AB；

(2)、如图②、图③，请分别写出线段DE，BC与AB之间的数量关系，不需要证明；

(3)、在（1）、（2）的条件下，AC $^{2}$ =100，AB-BC =2，则线段DE= ．

查看试题解析
27. 夏季来临，某商场准备购进甲、乙两种空调，其中甲种空调比乙种空调进价每台少500元，用40000元购进甲种空调数量与用50000元购进乙种空调数量相同．该商场计划一次性从空调生产厂家购进甲、乙两种空调共100台，其中乙种空调的数量不超过甲种空调的2倍．若甲种空调每台售价2400元，乙种空调每台售价3000元．请解答下列问题：

(1)、求甲、乙两种空调每台的进价分别是多少元?

(2)、设购进甲种空调x台，100台空调的销售总利润为y元，该商店购进甲、乙两种空调各多少台才能使销售总利润最大，最大利润是多少？

(3)、在（2）的条件下，商场拿出一部分利润购买A、B两种轮椅捐赠给敬老院，已知A种轮椅一台300元，B种轮椅一台400元，最后商场仅剩利润38600元，请直接写出商场有几种购买方案．

查看试题解析
28. 如图，直线y=-x+10与x轴、y轴分别交于点B和点C，点A的坐标为（8，0），点P（x，y）是直线上第一象限内的一个动点．

(1)、求△OPA的面积S与x的函数关系式，并直接写出自变量x的取值范围；

(2)、当△OPA的面积为10时，求点P的坐标；

(3)、在直线BC上是否存在点M，使以O，B，M为顶点的三角形是等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

查看试题解析