河北省石家庄市平山县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-29 类型:期末考试
一、单选题
-
1. 二次根式 的值等于( )A、-2 B、±2 C、2 D、42. 下列四组数据中,不能作为直角三角形三边长的是( )A、5,12,13 B、1,2,3 C、9,40,41 D、3,4,53. 下列计算正确的是( )A、 B、 C、 D、4. 某校篮球队5名场上队员的身高(cm)是:160,165,170,163,172,现用一名身高165cm的队员换下场上身高160cm的队员,与换人前相比,场上队员身高的( )A、平均数变小,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变小 D、平均数变大,方差变大5. 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()A、
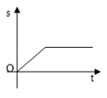 B、
B、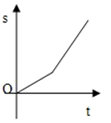 C、
C、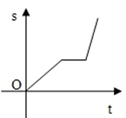 D、
D、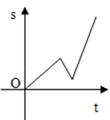 6. 检查一个门框(已知两组对边分别相等)是不是矩形,不可用的方法是( )A、测量两条对角线是否相等 B、用重锤线检查竖门框是否与地面垂直 C、测量两条对角线是否互相平分 D、测量门框的三个角是否都是直角7. 若k,m,n都是整数,且=k , =15 , =6 , 则下列关于k,m,n的大小关系,正确的是( )A、m<k<n B、m=n>k C、m<n<k D、k<m=n8. 对于一次函数y=-2x+4,下列结论错误的是( )A、函数值随自变量的增大而减小 B、当x<0时,y<4 C、函数的图象向下平移4个单位长度得y=-2x的图象 D、函数的图象与y轴的交点坐标是(0,4)9. 已知一次函数y=kx+b(k≠0)经过(2,﹣1)、(﹣3,4)两点,则它的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 已知一次函数y=kx+k,其在直角坐标系中的图象大体是( )A、
6. 检查一个门框(已知两组对边分别相等)是不是矩形,不可用的方法是( )A、测量两条对角线是否相等 B、用重锤线检查竖门框是否与地面垂直 C、测量两条对角线是否互相平分 D、测量门框的三个角是否都是直角7. 若k,m,n都是整数,且=k , =15 , =6 , 则下列关于k,m,n的大小关系,正确的是( )A、m<k<n B、m=n>k C、m<n<k D、k<m=n8. 对于一次函数y=-2x+4,下列结论错误的是( )A、函数值随自变量的增大而减小 B、当x<0时,y<4 C、函数的图象向下平移4个单位长度得y=-2x的图象 D、函数的图象与y轴的交点坐标是(0,4)9. 已知一次函数y=kx+b(k≠0)经过(2,﹣1)、(﹣3,4)两点,则它的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 已知一次函数y=kx+k,其在直角坐标系中的图象大体是( )A、 B、
B、 C、
C、 D、
D、 11. 如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
11. 如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )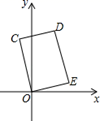 A、3 B、 C、 D、412. 如图,在菱形ABCD中,M,N分别在AB,CD上,且 , MN与AC交于点O,连接 , 若 , 则的度数为( )
A、3 B、 C、 D、412. 如图,在菱形ABCD中,M,N分别在AB,CD上,且 , MN与AC交于点O,连接 , 若 , 则的度数为( ) A、 B、 C、 D、13. 把直线 向上平移m个单位后,与直线 的交点在第一象限,则m的取值范围是( )A、1<m<7 B、3<m<4 C、m>1 D、m<414. 如图,已知直线l1:y=﹣2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(﹣2,0),则k的取值范围是( )
A、 B、 C、 D、13. 把直线 向上平移m个单位后,与直线 的交点在第一象限,则m的取值范围是( )A、1<m<7 B、3<m<4 C、m>1 D、m<414. 如图,已知直线l1:y=﹣2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(﹣2,0),则k的取值范围是( )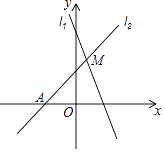 A、﹣2<k<2 B、﹣2<k<0 C、0<k<4 D、0<k<215. 如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,且CD= , 如果Rt△ABC的面积为1,则它的周长为( )
A、﹣2<k<2 B、﹣2<k<0 C、0<k<4 D、0<k<215. 如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,且CD= , 如果Rt△ABC的面积为1,则它的周长为( )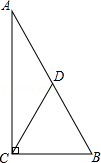 A、 B、+1 C、+2 D、+316. 正方形ABCD,正方形CEFG如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M.有下列结论:①EC=BP;②AP=AM:③∠BAP=∠GFP;④AB2+CE2= AF2;⑤S正方形ABCD+S正方形CGFE=2S△APF , 其中正确的是( )
A、 B、+1 C、+2 D、+316. 正方形ABCD,正方形CEFG如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M.有下列结论:①EC=BP;②AP=AM:③∠BAP=∠GFP;④AB2+CE2= AF2;⑤S正方形ABCD+S正方形CGFE=2S△APF , 其中正确的是( ) A、①②③ B、①③④ C、①②④⑤ D、①③④⑤
A、①②③ B、①③④ C、①②④⑤ D、①③④⑤二、填空题
-
17. 某公司招聘职员,竞聘者需通过计算机、语言表达和写作能力测试,李强的三项测试百分制得分依次是90分,80分,85分,其中计算机成绩占 , 语言表达占 , 写作能力成绩占 , 则李强最终的成绩是分.18. 如图,点E是菱形的边上一点,且 , 则 .
 19. 将正方形 , , 按如图所示方式放置,点 , , 和点 , , , 分别在直线和x轴上,则点的坐标是 , 的坐标是 .
19. 将正方形 , , 按如图所示方式放置,点 , , 和点 , , , 分别在直线和x轴上,则点的坐标是 , 的坐标是 .
三、解答题
-
20. 计算:(1)、;(2)、;(3)、;(4)、 .21. 月日是国际数学日,某校开展了一次数学趣味知识竞赛竞赛成绩为百分制 , 并随机抽取了名学生的竞赛成绩本次竞赛没有满分 , 经过整理数据得到以下信息:
信息一:名学生竞赛成绩频数分布表
分数
频数
信息二:成绩在这一组的是:
根据信息解答下列问题:
(1)、表中a= .(2)、成绩在这一组的众数是分,抽取的名学生竞赛成绩的中位数是 .(3)、若该校共有名学生参赛,请估计该校参赛学生成绩不低于分的约为人.22. 如图,在每个小正方形的边长均为一的方格纸中有线段AC和EF,点A,C,E,F均在小正方形的顶点上. (1)、在方格纸中画出一个以AC为对角线的菱形ABCD,点D在直线AC的下方,且点B,D都在小正方形的顶点上;(2)、在方格纸中画出以EF为底边,面积为6的等腰三角形EFG,且点G在小正方形的顶点上;(3)、在(1)(2)的条件下,连接DG,请直接写出线段DG的长.23. 在中, , D是的中点,E是的中点,过点A作AF//BC交的延长线于点F.
(1)、在方格纸中画出一个以AC为对角线的菱形ABCD,点D在直线AC的下方,且点B,D都在小正方形的顶点上;(2)、在方格纸中画出以EF为底边,面积为6的等腰三角形EFG,且点G在小正方形的顶点上;(3)、在(1)(2)的条件下,连接DG,请直接写出线段DG的长.23. 在中, , D是的中点,E是的中点,过点A作AF//BC交的延长线于点F. (1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.24. 如图,在直角坐标系xOy中,直线经过点 , 直线与交于点 , 与y轴交于点B,点A关于x轴对称的点在直线上.
(1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.24. 如图,在直角坐标系xOy中,直线经过点 , 直线与交于点 , 与y轴交于点B,点A关于x轴对称的点在直线上.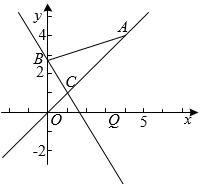 (1)、求直线的函数表达式;(2)、连接AB,求的面积;(3)、过点作x轴的垂线,分别交 , 于点M,N,若M,N两点间的距离不小于5,直接写出n的取值范围.25. 自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16 000元采购A型商品的件数是用7 500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.(1)、求一件A,B型商品的进价分别为多少元?(2)、若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数解析式,并写出m的取值范围;(3)、在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.26. 如图,已知一次函数y=﹣x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP.
(1)、求直线的函数表达式;(2)、连接AB,求的面积;(3)、过点作x轴的垂线,分别交 , 于点M,N,若M,N两点间的距离不小于5,直接写出n的取值范围.25. 自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16 000元采购A型商品的件数是用7 500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.(1)、求一件A,B型商品的进价分别为多少元?(2)、若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数解析式,并写出m的取值范围;(3)、在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.26. 如图,已知一次函数y=﹣x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP.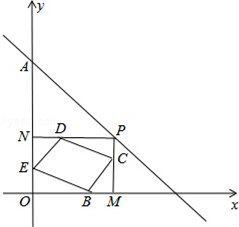 (1)、b=;(2)、求证:四边形BCDE是平行四边形;(3)、在直线y=﹣x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
(1)、b=;(2)、求证:四边形BCDE是平行四边形;(3)、在直线y=﹣x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.