河北省承德市高新区2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2022-08-29 类型:期末考试
一、单选题
-
1. 下列各式计算正确的( ).A、 B、 C、 D、2. 如图,中, , , 则BC的长为( )
 A、2 B、 C、 D、3. 某同学一周中每天体育运动所花时间(单位:分钟)分别为:35,39,45,40,55,48,45,这组数据的中位数是( ).A、35 B、40 C、45 D、554. 下列函数①;②;③;④;⑤中,是一次函数的有( ).A、1个 B、2个 C、3个 D、4个5. 如图,平面直角坐标系中,已知点 , , 以点A为圆心,AB长为半径画弧,交x铀的正半轴于点C,则C点的横坐标位于( ).
A、2 B、 C、 D、3. 某同学一周中每天体育运动所花时间(单位:分钟)分别为:35,39,45,40,55,48,45,这组数据的中位数是( ).A、35 B、40 C、45 D、554. 下列函数①;②;③;④;⑤中,是一次函数的有( ).A、1个 B、2个 C、3个 D、4个5. 如图,平面直角坐标系中,已知点 , , 以点A为圆心,AB长为半径画弧,交x铀的正半轴于点C,则C点的横坐标位于( ). A、4和5之间 B、3和4之间 C、5和6之间 D、2和3之间6. 已知平行四边形中, , 则的度数是( )A、 B、 C、 D、7. 一次函数的图象大致是( )A、
A、4和5之间 B、3和4之间 C、5和6之间 D、2和3之间6. 已知平行四边形中, , 则的度数是( )A、 B、 C、 D、7. 一次函数的图象大致是( )A、 B、
B、 C、
C、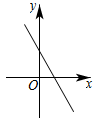 D、
D、 8. 一艘轮船以16海里/时的速度离开A港向北偏西30°方向航行,另一艘轮船同时以12海里/时的速度离开A港向北偏东60°方向航行,经过1.5小时后它位相距( )A、6海里 B、25海里 C、30海里 D、42海里9. 已知四边形是矩形,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
8. 一艘轮船以16海里/时的速度离开A港向北偏西30°方向航行,另一艘轮船同时以12海里/时的速度离开A港向北偏东60°方向航行,经过1.5小时后它位相距( )A、6海里 B、25海里 C、30海里 D、42海里9. 已知四边形是矩形,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( ) A、 B、 C、 D、10. 满足下列条件的三边长为a、b、c的 , 不是直角三角形的是( )A、 B、 C、 D、11. 下列二次根式中,可以与合并的是( ).A、 B、 C、 D、12. 甲、乙、丙、丁四人进行射击测试,四人10次射击成绩的平均数都是8.8环,方差分别为 , , , , 则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁13. 如图是我国数学家赵爽的股弦图,它由四个全等的直角三角形和小正方形拼成的一个大正方形.已知大正方形的面积是26,小正方形的面积是2,直角三角形的较短直角边长为a,较长直角边长为b,那么的值为( ).
A、 B、 C、 D、10. 满足下列条件的三边长为a、b、c的 , 不是直角三角形的是( )A、 B、 C、 D、11. 下列二次根式中,可以与合并的是( ).A、 B、 C、 D、12. 甲、乙、丙、丁四人进行射击测试,四人10次射击成绩的平均数都是8.8环,方差分别为 , , , , 则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁13. 如图是我国数学家赵爽的股弦图,它由四个全等的直角三角形和小正方形拼成的一个大正方形.已知大正方形的面积是26,小正方形的面积是2,直角三角形的较短直角边长为a,较长直角边长为b,那么的值为( ). A、28 B、50 C、26 D、16914. 如图,在四边形ABCD中, , , 对角线AC,BD交于点O,AC平分 , 过点C作交AB的延长线与点E,连接OE.
A、28 B、50 C、26 D、16914. 如图,在四边形ABCD中, , , 对角线AC,BD交于点O,AC平分 , 过点C作交AB的延长线与点E,连接OE.嘉嘉说:“四边形ABCD是菱形.”
琪琪说:“ . ”
对于他俩的说法,正确的是( )
 A、嘉嘉正确,琪琪错误 B、嘉嘉错误,琪琪正确 C、他俩都正确 D、他俩都错误15. 已知一次函数的图象上两点 , , 当时,有 , 那么m的值可能是( ).A、 B、 C、 D、16. 如图,已知直角三角形的直角边分别为a、b,斜边为c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形.那么,这四个图形中,直角三角形外,其他几个图形面积分别记作、、 .
A、嘉嘉正确,琪琪错误 B、嘉嘉错误,琪琪正确 C、他俩都正确 D、他俩都错误15. 已知一次函数的图象上两点 , , 当时,有 , 那么m的值可能是( ).A、 B、 C、 D、16. 如图,已知直角三角形的直角边分别为a、b,斜边为c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形.那么,这四个图形中,直角三角形外,其他几个图形面积分别记作、、 .
结论Ⅰ:、、满足只有(4);
结论Ⅱ:∵ , ∴的有(1)(2)(3).
对于结论Ⅰ和Ⅱ,判断正确的是( ).
A、Ⅰ对Ⅱ不对 B、Ⅰ不对Ⅱ对 C、Ⅰ和Ⅱ都对 D、Ⅰ和Ⅱ都不对二、填空题
-
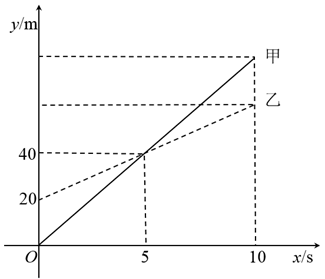
17. 小聪这学期的数学平时成绩90分,期中考试成绩80分,期末考试成绩82分,那么,小聪这学期数学平均成绩为分;若计算总评成绩的方法如下:平时成绩∶期中成绩∶期末成绩=3∶3∶4,则小聪总评成绩是分.18. 甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示,甲无人机的飞行速度为m/s;s时甲、乙两架无人机相距10m.
 19. 如图,正方形ABCD中, , 点E在CD边上,且 . 将沿AE对折至 , 延长EF交边BC于点G,连结AG、CF.则 , .
19. 如图,正方形ABCD中, , 点E在CD边上,且 . 将沿AE对折至 , 延长EF交边BC于点G,连结AG、CF.则 , .
三、解答题
-
20. 定义新运算: , 其中等号右边是常规的乘法和减法运算,
例如: .
(1)、计算:;(2)、有同学说:若 , 则 , 你是否同意他的观点,请说明理由.21. 如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且 , 连接DE、DF、BE、BF. (1)、求证:≌;(2)、若 , , 求四边形BEDF的面积.22. 如图所示,在中,点D为BC边上的一点, , , , .
(1)、求证:≌;(2)、若 , , 求四边形BEDF的面积.22. 如图所示,在中,点D为BC边上的一点, , , , . (1)、试说明;(2)、求AC的长及的面积;(3)、判断是否是直角三角形,并说明理由.23. 观察下列各式及其验证过程:
(1)、试说明;(2)、求AC的长及的面积;(3)、判断是否是直角三角形,并说明理由.23. 观察下列各式及其验证过程:, 验证:;
, 验证:;
(1)、按照上述两个等式及其验证过程的基本思路,猜想的变形结果并进行验证;(2)、针对上述各式反映的规律,写出用n(n为大于1的整数)表示的等式并给予验证.24. 某中学举行“书香进校园”知识竞赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.
平均数
中位数
众数
初中部
85
85
高中部
85
(1)、根据图示填写表格;(2)、结合两学部决赛成绩的平均数和中位数,分析哪个学部的决赛成绩较好.(3)、如果规定选手成绩较稳定的学部胜出,你认为哪个学部能胜出?请说明理由.25. 某公司准备组织20辆汽车将A、B、C三种水果共100吨运往外地销售.按计划,20辆车都要装运,每辆汽车只能装运同一种水果,且必须装满.根据下表提供的信息,解答以下问题:水果品种
A
B
C
每辆汽车运载量(吨)
6
5
4
每吨水果获利(元)
1400
1500
1200
(1)、设装运A种水果的车辆数为x,装运B种水果的车辆数为y,求y与x之间的函数关系式;(2)、如果装运每种水果的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;(3)、若要使此次销售获利最大,应采用哪种安排方案?并求出此时的最大利润.26. 如图,在平面直角坐标系中,过点 , 分别作x轴的垂线,垂足分别为A、B.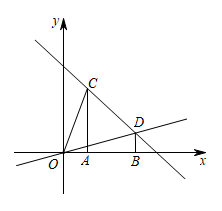 (1)、求直线CD和直线OD的解析式;(2)、点M为直线OD上的一个动点,过点M作x轴的垂线交x轴于点P,交直线CD于点N.
(1)、求直线CD和直线OD的解析式;(2)、点M为直线OD上的一个动点,过点M作x轴的垂线交x轴于点P,交直线CD于点N.①当PM为中位线时,求MN的长;
②是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由.