2022年苏科版初中数学七年级上册 2.6 有理数的乘法与除法（2）同步练习

试卷更新日期：2022-08-29 类型：同步测试

进入出卷网下载

一、夯实基础

1. 计算 $(- 12) \div (- 3)$ 的结果等于（）.

A、-15 B、-4 C、15 D、4

查看试题解析
2. 计算： $- 3 \div (- \frac{1}{2}) \div (- \frac{1}{2})$ 的结果是（）

A、﹣3 B、3 C、﹣12 D、12

查看试题解析
3. 若6□（﹣3）＝﹣2，则□表示的运算符号是（）

A、＋ B、﹣ C、× D、÷

查看试题解析
4. 已知43×47＝2021，则（﹣43） $\div \frac{1}{47}$ 的值为（）

A、2021 B、﹣2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
5. 若ab＜0，则 $\frac{a}{b}$ 的值（）

A、是正数 B、是负数 C、是非正数 D、是非负数

查看试题解析
6. 有理数a ， b在数轴上的对应点如图，下列式子：①a＞0＞b；②|b|＞|a|；③ab＜0；④a﹣b＞a+b；⑤ $\frac{a}{b}$ ＜﹣1，其中错误的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 一个数与 $- \frac{2}{3}$ 的积为9，则这个数是．

查看试题解析
8. 两个不相等的有理数a，b，若 $a + b = 0$ ，则 $\frac{a}{b}$ 的值是．

查看试题解析
9. 下列计算：①(-1)×(-2)×(-3)=6；②(-36)÷(-9)=-4；③ $\frac{2}{3} \times (- \frac{9}{4})$ ÷(-1)= $\frac{3}{2}$ ；④(-4) ÷ $\frac{1}{2}$ ×( -2) =16，其中正确的有个

查看试题解析
10. 从-3，-2，-1，4，5中任取2个数相乘，所得积中的最大值为a，最小值为b，则 $\frac{a}{b}$ 的值为.

查看试题解析
11. （1）两数的积是1，已知一个数是-237 ，求另一个数；
1. （2）两数的商是 $- 3 \frac{1}{2}$ ，已知被除数是 $4 \frac{1}{2}$ ，求除数．
查看试题解析
12. 请你先认真阅读材料：
计算 $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$

解：原式的倒数是 $(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \div (- \frac{1}{30})$

＝ $(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \times (- 30)$

＝ $\frac{2}{3}$ ×（﹣30）﹣ $\frac{1}{10}$ ×（﹣30）+ $\frac{1}{6}$ ×（﹣30）﹣ $\frac{2}{5}$ ×（﹣30）

＝﹣20﹣（﹣3）+（﹣5）﹣（﹣12）

＝﹣20+3﹣5+12

＝﹣10

故原式等于﹣ $\frac{1}{10}$

再根据你对所提供材料的理解，选择合适的方法计算： $(- \frac{1}{42}) \div (\frac{1}{6} - \frac{3}{14} + \frac{2}{3} - \frac{2}{7})$ ．

查看试题解析
13. 小丽有5张写着不同数字的卡片(如图2－6－2)，请你按要求抽取卡片，完成下列各问题：
图2－6－2

(1)、从中取出3张卡片，如何抽取才能使这3张卡片上的数字先让两个数相乘再与第三个数相除的结果最大？最大值是多少？

(2)、从中取出3张卡片，如何抽取才能使这3张卡片上的数字先让两个数相除再与第三个数相乘的结果最小？最小值是多少？

查看试题解析
14. 初一某班有60名学生，周练分数超过90分的部分用正分表示，不足90分的部分用负分表示，在一次周练后，数学老师对全班同学的成绩做了如下统计：

与90分的差值（单位：分）

-26

-18

-8

0

8

15

人数

4

8

12

18

10

8

(1)、该班的最高分与最低分相差；

(2)、该班成绩低于90分的同学占全班同学的百分比是多少？

(3)、计算出该班这次数学周练的平均成绩．

查看试题解析

二、能力提优

15. 在小数0.28里面有28个（）

A、0.1 B、0.01 C、0.001 D、0.0001

查看试题解析
16. 下列运算正确的是（）

A、﹣9÷2× $\frac{1}{2}$ ＝﹣9 B、6÷（ $\frac{1}{3}$ ﹣ $\frac{1}{2}$ ）＝﹣1 C、1 $\frac{1}{4}$ ﹣1 $\frac{1}{4}$ ÷ $\frac{5}{6}$ ＝0 D、﹣ $\frac{1}{2}$ ÷ $\frac{1}{4}$ ÷ $\frac{1}{4}$ ＝﹣8

查看试题解析
17. 已知a＜-1，那么 $\frac{| a - 1 |}{| a | - 1}$ 的值是（）．

A、等于1 B、小于零 C、等于 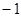D、大于零

查看试题解析
18. 设n！表示所有小于或等于该数的正整数的积，如4！=1×2×3×4，则计算 $\frac{101 ！ - 100 ！}{99 ！ + 98 ！}$ 的结果为（）

A、100 B、99 C、10 000 D、9 900

查看试题解析
19. 如图，点A，B，C，D四个点在数轴上表示的数分别为a，b，c，d，则下列结论中，错误的是（）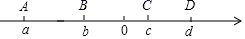

A、 $a + c < 0$ B、 $b - a > 0$ C、 $a c > 0$ D、 $\frac{b}{d} < 0$

查看试题解析
20. 在下列各题中，结论正确的是（）

A、若 $a < 0, b < 0$ ，则 $\frac{b}{a} > 0$ B、若 $a > b$ ，则 $a - b > 0$ C、若 $a < 0, b < 0$ ，则 $a b < 0;$ D、若 $a > b, a > 0$ ，则 $\frac{b}{a} < 0$

查看试题解析
21. 若abc≠0，则 $\frac{| a |}{a}$ ＋ $\frac{| b |}{b}$ + $\frac{c}{| c |}$ 的值为（）

A、±3或±1 B、±3或0或±1 C、±3或0 D、0或±1

查看试题解析
22. 若 $\frac{a}{b} > 0$ ， $\frac{b}{c} < 0$ ，则 $a c$ 0（填“>”、“<”或“=”）

查看试题解析
23. 已知|x|＝3，|y|＝ $\frac{1}{5}$ ，且xy＜0，则 $\frac{x}{y}$ ＝．

查看试题解析
24. 若规定“!”是一种数学运算符号，且 $1! = 1, 2! = 2 \times 1 = 2, 3! = 3 \times 2 \times 1 = 6, 4 \times 3 \times 2 \times 1 = 24, \dots$ 则 $\frac{100!}{98!}$ 的值为

查看试题解析
25. 已知 $a$ 是有理数， $[a]$ 表示不超过 $a$ 的最大整数，如 $[3.2] = 3$ ， $[- 1.5] = - 2$ ， $[0.8] = 0$ ， $[2] = 2$ 等，那么 $[3.14] \div [3] \times [- 5 \frac{1}{2}] =$ .

查看试题解析
26. 小华在课外书中看到这样一道题：
计算： $\frac{1}{36} \div$ （ $\frac{1}{4} + \frac{1}{12} - \frac{7}{18} - \frac{1}{36}$ ）+（ $\frac{1}{4} + \frac{1}{12} - \frac{7}{18} - \frac{1}{36}$ ） $\div \frac{1}{36}$ ．
她发现，这个算式反映的是前后两部分的和，而这两部分之间存在着某种关系，利用这种关系，她顺利地解答了这道题

(1)、前后两部分之间存在着什么关系？

(2)、先计算哪部分比较简便？并请计算比较简便的那部分．

(3)、利用（1）中的关系，直接写出另一部分的结果．

(4)、根据以上分析，求出原式的结果．

查看试题解析
27. 已知三个有理数a，b，c的积是负数，它们的和是正数，当x= $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 时，求代数式： x²⁰¹⁹-2x+2的值.

查看试题解析

三、延伸拓展

28. 如果 a 、 b 、 c 为有理数，且 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} = - 1$ ，则 $\frac{a b c}{| a b c |}$ 的值为（）

A、-3 B、1 C、-1 D、3

查看试题解析
29. 下列说法：
①2018个有理数相乘，其中负数有2005个，那么所得的积为负数②若m满足|m|＋m＝0则m<0③有理数 $\frac{b}{a}$ 的倒数是 $\frac{a}{b}$ ④若三个有理数a，b，c满足 $\frac{| a b |}{a b} + \frac{| a c |}{a c} + \frac{| b c |}{b c}$ =-1，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = - 1$ 其中正确的是有（）个

A、0 B、1 C、2 D、3

查看试题解析
30. 下列说法正确的是（填序号）
①若 $| a | = b$ .则一定有 $a = \pm b$ ；②若 $a$ ， $b$ 互为相反数，则 $\frac{b}{a} = - 1$ ；③几个有理数相乘，若负因数有偶数个，那么他们的积为正数；④两数相加，其和小于每一个加数，那么这两个加数必是两个负数：⑤0除以任何数都为0；⑥若 $| x - 3 | + | x + 2 | = 5$ ，则 $- 2 \leq x \leq 3$ .

查看试题解析

与90分的差值（单位：分）	-26	-18	-8	0	8	15
人数	4	8	12	18	10	8

2022年苏科版初中数学七年级上册 2.6 有理数的乘法与除法（2） 同步练习

一、夯实基础

二、能力提优

三、延伸拓展

2022年苏科版初中数学七年级上册 2.6 有理数的乘法与除法（2）同步练习