2022-2023浙教版数学七年级上册2.6有理数的混合运算课后测验

试卷更新日期：2022-08-28 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 河里水位第一天上升 $38 cm$ ，第二天下降 $37 cm$ ，第三天又下降 $39 cm$ ，第四天上升 $33 cm$ ，则此时的水位比开始水位高（）

A、 $5 cm$ B、 $- 5 cm$ C、 $1 cm$ D、 $- 6 cm$

查看试题解析
2. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”．一位书生坚持每天五更起床读书，为了勉励自己，他用“结绳记数”的方法来记录自己读书的天数，如图1是他从右到左依次排列的绳子上打结，满六进一，表示的天数为 $51$ 天（ $1 \times 6^{2} + 2 \times 6 + 3 = 51$ ），按同样的方法，图2表示的天数是（　　　）

A、 $48$ B、 $46$ C、 $236$ D、 $92$

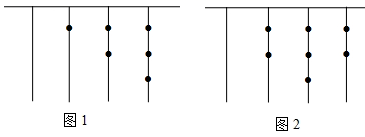查看试题解析
3. 下表是某地区11月份连续四天最高气温与最低气温情况，这四天温差最大的是（）
某地区
星期一
星期二
星期三
星期四
最高气温（℃）
8
12
10
9
最低气温（℃）
1
1
-1
-3

A、星期一 B、星期二 C、星期三 D、星期四

查看试题解析
4. 下列计算中，正确的是（）

A、 $\frac{1}{2} - \frac{1}{2} \times 3 = 0 \times 3 = 0$ B、 $74 - 2^{2} \div 70 = 70 \div 70 = 1$ C、 $6 \div (\frac{3}{2} - \frac{2}{3}) = 6 \div \frac{5}{6} = \frac{36}{5}$ D、 ${(- 3)}^{2} - {(- 2)}^{3} = 9 - 8 = 1$

查看试题解析
5. 如图是一个“数值转换机”，按下面的程序输入一个数 $x$ ，若输入的数 $x = - 2$ ，则输出结果为（）

A、0 B、2 C、4 D、-4

查看试题解析
6. 定义一种新运算a⊙b＝（a+b）×2，计算（﹣5）⊙3的值为（）

A、﹣7 B、﹣1 C、1 D、﹣4

查看试题解析

7. 某路公交车从起点经过A ， B ， C ， D站到达终点，各站上、下乘客人数如下表所示（用正数表示上车的人数，负数表示下车的人数）：

站点	起点	A	B	C	D	终点
上车人数	x	15	12	7	5	0
下车人数	0	－3	－4	－10	－11	-29

若此公交车采用一票制，即每位上车乘客无论哪站下车，车票都是2元，问该车这次出车共收入（）

A、114元 B、228元 C、78元 D、56元

查看试题解析

8. 用2，0，2，2这四个数进行如下运算，计算结果最小的式子是 $($ $)$

A、 $2 - 0 \times 2 + 2$ B、 $2 - 0 + 2 \times 2$ C、 $2 \times 0 + 2 - 2$ D、 $2 + 0 - 2 \times 2$

查看试题解析
9. 如图，已知正方形的边长为24厘米，甲，乙两动点分别从正方形ABCD的顶点D，B同时沿正方形的边开始移动，甲点按顺时针方向环行，乙点按逆时针方向环行，若乙的速度为9厘米/秒，甲的速度为3厘米/秒，当它们运动了2022秒时，它们在正方形边上相遇了（）

A、252 次 B、253次 C、254次 D、255次

查看试题解析
10. 小新玩“24 点”游戏，游戏规则是对数进行加、减、乘、除混合运算（每张卡片只能用一次，可以加括号）使得运算结果是 24 或－24．小新已经抽到前3 张卡片上的数字分别是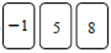，若再从下列 4 张中抽出 1 张，则其中不能与前 3 张算出“24 点”的是（）

A、 B、 C、 D、

查看试题解析

二、填空题（每空2分，共14分）

11. 某地星期一上午的温度是17℃，中午又上升了8℃，下午由于冷空气南下，到夜间又下降了10℃，则这天夜间的温度是 ℃．

查看试题解析
12. 在 $- 4$ □5的“□”中填入一个运算符号“ $+$ 、 $-$ 、 $\times$ 、 $\div$ ”，则最小的运算结果是．

查看试题解析
13. 观察下面两行数：
-2，4，-8，16，-32，64，…

1，7，-5，19，-29，67，…根据你发现的规律，取每行数的第9个数，它们的和等于.

查看试题解析
14. 如图，某学校“桃李餐厅”把WIFI密码做成了数学题．小红在餐厅就餐时，思索了一会儿，输入密码，顺利地连接到了“桃李餐厅”的网络．那么她输人的密码是 .

查看试题解析
15. 已知某快递公司的收费标准为：寄一件物品不超过5千克，收费13元；超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品，需要付费元.

查看试题解析
16. 如图是一个有理数混合运算的程序流程图.

①当输入数x为0时，输出数y是.

②已知输入数x为负整数，且整个运算流程总共进行了两轮后，循环结束，输出数y. 则输入数x最大值为.

查看试题解析

三、计算题（共2题，共14分）

17. 计算：

(1)、-1-[6-(-11)+(-8)]

(2)、(-10)×( $- \frac{1}{4}$ )×(-0.1)

(3)、6.868×7+68.68×(-1.7)

(4)、-1²+(3-5)²

查看试题解析
18. 计算：

(1)、 $- 3^{2} - (- 8) \times {(- 1)}^{5} \div {(- 1)}^{4}$ ；

(2)、 $- 1^{2} + {(- 1 \frac{1}{2})}^{3} \div \frac{3}{4} - | 0.25 - \frac{3}{8} |$

(3)、 $(\frac{2}{3} - \frac{3}{4} + \frac{1}{6}) \div (- \frac{1}{24})$

查看试题解析

四、解答题（共6题，共42分）

19. 阅读下面解题过程：
计算： $(- 15) \div (\frac{1}{3} - \frac{3}{2} - 3) \times 6$

解：原式＝ $(- 15) \div (- \frac{25}{6} \times 6)$ （第一步）＝（﹣15）÷（﹣25）（第二步）＝ $- \frac{3}{5}$ （第三步）

回答：

(1)、上面解题过程中有两个错误，第一处是第步，错误的原因是，第二处是第步，错误的原因是；

(2)、正确的结果是.

查看试题解析
20. 小明过年得到2000元的压岁钱，存入银行，准备到期后的利息捐给希望工程．已知三年定期存款的年利率为2.25%，那么三年后小明可捐给希望工程多少钱？（国家规定要收取20%的利息税）．

查看试题解析
21. 某出租车沿南北方向行驶，从A地出发，晚上到达B地．规定向北为正方向．行驶记录如下（单位：㎞）：+18、-9、+7、-14、-6、+13、-6，

(1)、B地在A地的什么位置？

(2)、若出租车每行驶1㎞耗油1升，求该天共耗油多少升？

(3)、若出租车起步价为7元，起步里程为3千米（包括3千米），超过部分每千米1.2元，则该天车费多少元？

查看试题解析
22. 王红有5张写着以下数字的卡片，请按要求抽出卡片，完成下列各题：

(1)、从中抽取2张卡片，使这两张卡片上的数字乘积最大，乘积的最大值为.

(2)、从中抽取除0以外的4张卡片，将这4个数字进行加、减、乘、除等混合运算，使其结果等于24，每个数字只能用一次，请写出两种不同的符合要求的运算式子.

查看试题解析

23. 国庆黄金周电影《长津湖》成为了浙江人民观影的首选，宁波某区9月30日该电影票的售票量为

1.1

万张，该区10月1日到10月7日售票量的变化如下表（正号表示售票量比前一天多，负号表示售票量比前一天少）：

日期	1 日	2 日	3 日	4 日	5 日	6 日	7 日
售票量的变化（单位：万张）	+0.5	+0.1	-0.3	-0.2	+0.4	-0.2	+0.1

请根据以上信息，回答下列问题：

(1)、10月2日的售票量为多少万张?

(2)、10月7日与9月30日相比较，哪一天的售票量多? 多多少万张?

(3)、若平均每张票价为50元，则10月1日到10月7日该区销售

《

长津湖》电影票共收入多少万元?