2022-2023学年冀教版数学九年级上册第24章一元二次方程单元测试卷

试卷更新日期：2022-08-26 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 关于x的一元二次方程 $x^{2} - m = 0$ 的一个根是3，则m的值是（）

A、3 B、 $- 3$ C、9 D、 $- 9$

查看试题解析
2. 一元二次方程 $x^{2} + x - 3 = 0$ 的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
3. 下列方程中，是关于x的一元二次方程是（）

A、 $a x^{2} + b x + c = 0$ B、 $\frac{1}{x^{2}} + \frac{1}{x} - 2 = 0$ C、 $3 x^{2} = 2 (x + 1)$ D、 $x^{2} + 2 x = x^{2} - 1$

查看试题解析
4. 某中学组织九年级学生篮球比赛，以班为单位，每两班之间都比赛一场，总共安排15场比赛，则共有多少个班级参赛（）

A、6 B、5 C、4 D、3

查看试题解析
5. 方程 $x^{2} + 2 x = 1$ 的左边配成完全平方后所得方程为（）

A、 ${(x + 1)}^{2} = 2$ B、 ${(x - 1)}^{2} = 2$ C、 ${(x + 1)}^{2} = 1$ D、 ${(x - 1)}^{2} = 1$

查看试题解析
6. 已知 $a ， b$ 是关于 $x$ 的方程 $x^{2} + 3 x - 2009 = 0$ 的两根，则 $a^{2} - a - 4 b$ 的值是（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
7. 直线y= $x$ +a不经过第四象限，则关于 $x$ 的方程a $x^{2}$ -2 $x$ -1=0的实数解的个数是（）

A、0个 B、1个 C、2个 D、1个或2个

查看试题解析
8. 若关于x的方程 ${(^{} + 2 x)}^{2} + 2 (x^{2} + 2 x) - 8 = 0$ 有实数根，则 $x^{2} + 2 x$ 的值为（）

A、－4 B、2 C、－4或2 D、4或－2

查看试题解析
9. 已知直角三角形的两条边长分别是方程x²﹣9x+20＝0的两个根，则此三角形的第三边是（）

A、4或5 B、3 C、 $\sqrt{41}$ D、3或 $\sqrt{41}$

查看试题解析
10. 为落实教育优先发展，南充市财政一般公共预算2019年教育经费投入93.15亿元，2021年教育经费投入99.45亿元，设南充市财政一般公共预算教育经费投入年平均增长率为x，则可列方程为（）

A、 $93.15 {(1 + x)}^{2} = 99.45$ B、 $93.15 {(1 + x)}^{3} = 99.45$ C、 $93.15 (1 + 2 x) = 99.45$ D、 $93.15 (1 + 3 x) = 99.45$

查看试题解析

二、填空题（每题4分，共24分）

11. $(a - 2) x^{a^{2} - 2} + 3 x - 1 = 0$ 是关于 $x$ 的一元二次方程，则 $a$ 的值是.

查看试题解析
12. 设x₁ ， x₂是方程x²－3x－1＝0的两个根，则x₁＋x₂＝， x₁x₂＝.

查看试题解析
13. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个不相等的实数根，则实数 $m$ 的取值范围是.

查看试题解析
14. 定义：关于x的方程 $a_{1} x^{2} + b_{1} x + c_{1} = 0$ （a₁≠0）与 $a_{2} x^{2} + b_{2} x + c_{2} = 0$ （a₂≠0），如果满足a₁+a₂＝0，b₁＝b₂ ， c₁+c₂＝0，则称这两个方程互为“对称方程”．若关于x的方程 $3 x^{2} + (m^{2} - 2 m + 3) x - 4 = 0$ 与 $- 3 x^{2} + 2 x + n = 0$ 互为“对称方程”，则 $(m - n)^{2}$ 的值为．

查看试题解析
15. 某树主干长出x根枝干，每个枝干又长出x根小分支，若主干、枝干和小分支总数共133根，则主干长出枝干的根数x为．

查看试题解析
16. 学校组织一次乒乓球赛，要求每两队之间都要比赛一场．若共赛了28场，设有 $x$ 个球队参赛，根据题意列出x满足的关系式为．

查看试题解析

三、计算题（共2题，共16分）

17. 用适当的方法解下列方程.

(1)、 ${(2 x + 3)}^{2} - 16 = 0$ ；

(2)、 ${(2 x + 1)}^{2} = 3 (2 x + 1)$ .

查看试题解析
18. 用指定的方法解下列方程：

(1)、 $x^{2} + 4 x + 1 = 0$ （配方法）

(2)、 $2 x^{2} + 3 x - 1 = 0$ （公式法）

查看试题解析

四、解答题

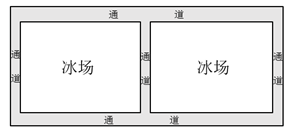
19. 已知关于x的一元二次方程x²﹣x+2m﹣4＝0有两个实数根．

(1)、求m的取值范围；

(2)、若方程的两根满足（x₁﹣3）（x₂﹣3）＝m²﹣1，求m的值．

查看试题解析
20. 某校举办了“冰雪运动进校园”活动，计划在校园一块矩形的空地上铺设两块完全相同的矩形冰场．如下图所示，已知空地长27m，宽12m，矩形冰场的长与宽的比为4：3，如果要使冰场的面积是原空地面积的 $\frac{2}{3}$ ，并且预留的上、下通道的宽度相等，左、中、右通道的宽度相等，那么预留的上、下通道的宽度和左、中、右通道的宽度分别是多少米？

查看试题解析
21. 第24届冬季奥林匹克运动会将于2022年2月4日在北京开幕，北京成为历史上第一个既举办夏奥会又举办冬奥会的城市．某批发商最近订购了一批具有纪念意义的书签进行销售，平均每天可售出500张，每张可获利0.5元．调查发现，如果每张书签的售价每降价0.1元，平均每天可多售出200张．批发商要想平均每天获利270元，求每张书签应降价多少元．

查看试题解析
22. 随着全球疫情的扩散，疫苗需求仍存在较大缺口，某制药企业及时引进一条疫苗生产线生产新冠疫苗，开工第一天生产疫苗10000盒，第三天生产疫苗12100盒，若每天增长的百分率相同.

(1)、求每天增长的百分率.

(2)、经调查发现，1条生产线的最大产能是15000盒/天，若每增加1条生产线，则每条生产线的产能将减少500盒/天，现该厂要保证每天生产疫苗105000盒，在增加产能的同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

查看试题解析
23. 如图①，某校进行校园改造，准备将一块正方形空地划出部分区域栽种鲜花，原空地一边减少了4m，另一边减少了5m，剩余部分面积为650m² ．

(1)、求原正方形空地的边长；

(2)、在实际建造时，从校园美观和实用的角度考虑，按图②的方式进行改造，先在正方形空地一侧建成1m宽的画廊，再在余下地方建成宽度相等的两条小道后，其余地方栽种鲜花，如果栽种鲜花区域的面积为812m² ，求小道的宽度．

查看试题解析
24. 如图，四边形 ACDE 是证明勾股定理时用到的一个图形，a 、b 、c 是 Rt△ABC和 Rt△BED 的边长，已知 $A E = \sqrt{2} c$ ，这时我们把关于 x 的形如 $a x^{2} + \sqrt{2} c x + b = 0$ 二次方程称为“勾系一元二次方程”.

请解决下列问题：

(1)、写出一个“勾系一元二次方程”；

(2)、求证：关于 x 的“勾系一元二次方程” $a x^{2} + \sqrt{2} c x + b = 0$ ，必有实数根；

(3)、若 x = -1是“勾系一元二次方程” $a x^{2} + \sqrt{2} c x + b = 0$ 的一个根，且四边形 ACDE 的周长是6 $\sqrt{2}$ ，求△ABC的面积.

查看试题解析

2022-2023学年冀教版数学九年级上册第24章 一元二次方程 单元测试卷

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、计算题（共2题，共16分）

四、解答题

2022-2023学年冀教版数学九年级上册第24章一元二次方程单元测试卷