2022-2023学年冀教版数学九年级上册24.4.1一元二次方程的应用之传染问题+几何问题同步测试

试卷更新日期：2022-08-26 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 某中学组织九年级学生篮球比赛，以班为单位，每两班之间都比赛一场，总共安排15场比赛，则共有多少个班级参赛（）

A、6 B、5 C、4 D、3

查看试题解析
2. 如图所示，在一边靠墙（墙足够长）的空地上，修建一个面积为375平方米的矩形临时仓库，仓库一边靠墙，另外三边用总长为55米的栅栏围成，若设栅栏AB的长为x米，则下列各方程中，正确的是（）

A、 $\frac{1}{2}$ x（55﹣x）＝375 B、 $\frac{1}{2}$ x（55﹣2x）＝375 C、x（55﹣2x）＝375 D、x（55﹣x）＝375

查看试题解析
3. 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是157，每个支干长出的小分支数目为（）

A、12 B、11 C、8 D、7

查看试题解析
4. 用一条长 $60 c m$ 的绳子围成一个面积为 $200 c m^{2}$ 的长方形．设长方形的长为 $x c m$ ，则可列方程为（）

A、 $x (30 - x) = 200$ B、 $x (30 + x) = 200$ C、 $x (60 + x) = 200$ D、 $x (60 - x) = 200$

查看试题解析
5. 一个同学经过培训后会做某项实验，回到班级后第一节课他教会了若干个同学，第二节课会做的同学每人又教会了同样多的同学，这样全班共有36人会做这项实验，若设1人每次能教会x名同学，则可列方程为（）

A、x＋（x＋1）x＝36 B、（x＋1）²＝36 C、1＋x＋x²＝36 D、x＋（x＋1）²＝36

查看试题解析
6. 某地区计划举行校际篮球友谊赛，赛制为主客场形式（每两队之间在主客场各比赛一场），已知共比赛了30场次，则共有（　　）支队伍参赛．

A、4 B、5 C、6 D、7

查看试题解析
7. 小亮、小明、小刚三名同学中，小亮的年龄比小明的年龄小2岁，小刚的年龄比小明的年龄大1岁，并且小亮与小刚的年龄的乘积是130.你知道这三名同学的年龄各是多少岁吗？设小明的年龄为x岁，则可列方程为（）

A、 $(x + 2) (x - 1) = 130$ B、 $(x - 2) (x + 1) = 130$ C、 $x (x - 2) = 130$ D、 $x (x + 1) = 130$

查看试题解析
8. 早期，甲肝流行，在一天内，一人能传染4人，若有三人患上甲肝，那么经过两天患上甲肝的人数为（）

A、50 B、75 C、25 D、70

查看试题解析
9. 如图所示，A，B，C，D为矩形的四个顶点，AB=16cm，AD=8cm，动点P，Q分别从点A，C同时出发，点P以3cm/s的速度向B移动，一直到达B为止；点Q以2cm/s的速度向D移动．当P，Q两点从出发开始几秒时，点P和点Q的距离是10cm．(若一点到达终点，另一点也随之停止运动)（）

A、2s或 $\frac{23}{5}$ s B、1s或 $\frac{22}{5}$ s C、 $\frac{22}{5}$ s D、2s或 $\frac{22}{5}$ s

查看试题解析
10. 如图， $R t Δ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 6$ cm， $B C = 8$ cm，动点 $P$ 从点 $A$ 出发沿 $A B$ 边以 $1$ cm /秒的速度向点 $B$ 移动，点 $Q$ 从点 $B$ 出发，沿 $B C$ 边以 $2$ cm /秒的速度向点 $C$ 移动，如果点 $P$ ， $Q$ 分别从点 $A$ ， $B$ 同时出发，在运动过程中，设点 $P$ 的运动时间为 $t$ ，则当 $Δ B P Q$ 的面积为 $8$ cm²时， $t$ 的值（）

A、2或3 B、2或4 C、1或3 D、1或4

查看试题解析

二、填空题（每题4分，共20分）

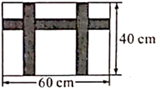
11. 我国南宋数学家杨辉所著《田亩比类乘除捷法》中记载了这样一道题：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步．”其大意为：一个矩形的面积为864平方步，宽比长少12步，问宽和长各多少步？设矩形的宽为x步，根据题意，可列方程为．

查看试题解析
12. 某公司展销如图所示的长方形工艺品，该工艺品长60cm，宽40cm，中间镶有宽度相同的三条丝绸花边，若丝绸花边的面积为650cm² ，设花边的宽度为xcm.根据题意得方程.

查看试题解析
13. 2021年10月10日，第七届黑龙江绿色食品产业博览会开幕，虎林市组建团队参加，为增进了解，在参加会议前团队每两个人间互送了一次名片，一共送出90张名片，则这个团队有人．

查看试题解析
14. 参加一次同学聚会，每两人都握一次手，所有人共握了15次，若设共有x人参加同学聚会．列方程得．

查看试题解析
15. 定义：关于x的方程 $a_{1} x^{2} + b_{1} x + c_{1} = 0$ （a₁≠0）与 $a_{2} x^{2} + b_{2} x + c_{2} = 0$ （a₂≠0），如果满足a₁+a₂＝0，b₁＝b₂ ， c₁+c₂＝0，则称这两个方程互为“对称方程”．若关于x的方程 $3 x^{2} + (m^{2} - 2 m + 3) x - 4 = 0$ 与 $- 3 x^{2} + 2 x + n = 0$ 互为“对称方程”，则 $(m - n)^{2}$ 的值为．

查看试题解析

三、解答题（每题10分，共50分）

16. 学校生物小组有一块长32m，宽20m的矩形实验田，为了管理方便，准备沿平行于两边的方向纵、横个开辟一条等宽的小道，要使种植面积为540m² ，小道的宽应是多少米？

查看试题解析
17. 列方程（组）解应用题：某驻村工作队，为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下，围一块面积为600m²的矩形试验茶园，便于成功后大面积推广．如图所示，茶园一面靠墙，墙长35m，另外三面用69m长的篱笆围成，其中一边开有一扇1m宽的门（不包括篱笆）．求这个茶园的长和宽．

查看试题解析
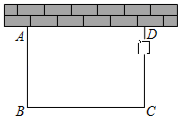18. 如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？

查看试题解析
19. 请根据图片内容，回答下列问题：

我叫Omicron（奥密克戎），是新冠病毒的变异毒株，我的传染性很强，传播速度很快。有一次我感染了1个人，此人未被有效隔离，经过两轮传染后共有121名感染者．

(1)、每轮传染中，平均一个人传染了几个人？

(2)、按照这样的速度传染，第三轮将新增多少名感染者（假设每轮传染人数相同）？

查看试题解析
20. 有一块长28cm，宽12cm的矩形铁皮．

(1)、如图1，如果在铁皮的四个角裁去四个边长一样的正方形后，将其折成底面积为192cm²的无盖长方体盒子，求裁去的正方形的边长．

(2)、由于需要，计划制作一个有盖的长方体盒子，为了合理利用材料，某学生设计了如图2的裁剪方案，阴影部分为裁剪下来的边角料，其中左侧的两个阴影部分为正方形，若剩余部分恰好能折成一个底面积为130cm²的有盖盒子，请你求出裁去的左侧正方形的边长．

查看试题解析

2022-2023学年冀教版数学九年级上册24.4.1一元二次方程的应用之传染问题+几何问题 同步测试

一、单选题（每题3分，共30分 ）

二、填空题（每题4分，共20分）

三、解答题（每题10分，共50分）

2022-2023学年冀教版数学九年级上册24.4.1一元二次方程的应用之传染问题+几何问题同步测试

一、单选题（每题3分，共30分）