河北省廊坊市香河县2021-2022学年高二下学期数学期末试卷
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 已知全集 , 函数的定义域为M,集合 , 则下列结论正确的是( )A、 B、 C、 D、2. 下列说法中正确的是( )A、“”是“”的必要不充分条件 B、命题“对 , 恒有”的否定是“ , 使得” C、在同一直角坐标系中,函数与的图象关于直线对称 D、若幂函数过点 , 则3. 随着人们生活水平的提高,产生的垃圾也越来越多,而进行垃圾分类管理能将这些垃圾转化为新能源,同时还能让这些垃圾得到有效的处理,这样能减少对土壤的危害,防止污染空气,但是人们对垃圾分类知识了解不多,所以某社区通过公益讲座的形式对社区居民普及垃圾分类知识,为了解讲座的效果,随机抽取了10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图所示,则( )
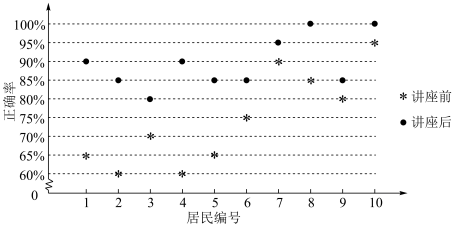 A、讲座前问卷答题的正确率的中位数小于70% B、讲座后问卷答题的正确率的平均数大于85% C、讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差 D、讲座后问卷答题的正确率的极差大于讲座前正确率的极差4. 如图所示,在长方体中, , 点E是棱的中点,则点E到平面的距离为( )
A、讲座前问卷答题的正确率的中位数小于70% B、讲座后问卷答题的正确率的平均数大于85% C、讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差 D、讲座后问卷答题的正确率的极差大于讲座前正确率的极差4. 如图所示,在长方体中, , 点E是棱的中点,则点E到平面的距离为( ) A、1 B、 C、 D、5. 函数 的图像可能是( )A、
A、1 B、 C、 D、5. 函数 的图像可能是( )A、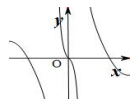 B、
B、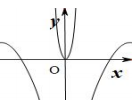 C、
C、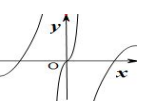 D、
D、 6. 某病毒研究所为了更好地研究“新冠”病毒,计划改建十个实验室,每个实验室的改建费用分为装修费和设备费,每个实验室的装修费都一样,设备费从第一到第十实验室依次构成等比数列,已知第五实验室比第二实验室的改建费用高42万元,第七实验室比第四实验室的改建费用高168万元,并要求每个实验室改建费用不能超过1700万元.则该研究所改建这十个实验室投入的总费用最多需要( )A、3233万元 B、4706万元 C、4709万元 D、4808万元7. 已知的两个极值点分别为且 , 则函数( )A、-1 B、 C、1 D、与b有关8. 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设 , 用表示不超过的最大整数,则称为高斯函数,例如: , , 已知函数 , , 则下列叙述正确的是( )A、是偶函数 B、在上是增函数 C、的值域是 D、的值域是
6. 某病毒研究所为了更好地研究“新冠”病毒,计划改建十个实验室,每个实验室的改建费用分为装修费和设备费,每个实验室的装修费都一样,设备费从第一到第十实验室依次构成等比数列,已知第五实验室比第二实验室的改建费用高42万元,第七实验室比第四实验室的改建费用高168万元,并要求每个实验室改建费用不能超过1700万元.则该研究所改建这十个实验室投入的总费用最多需要( )A、3233万元 B、4706万元 C、4709万元 D、4808万元7. 已知的两个极值点分别为且 , 则函数( )A、-1 B、 C、1 D、与b有关8. 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设 , 用表示不超过的最大整数,则称为高斯函数,例如: , , 已知函数 , , 则下列叙述正确的是( )A、是偶函数 B、在上是增函数 C、的值域是 D、的值域是二、多选题
-
9. 已知复数 , 为z的共轭复数,复数 , 则下列结论正确的是( )A、对应的点在复平面的第二象限 B、 C、的实部为 D、的虚部为10. 在中,点满足 , 当点在线段上(不含点)移动时,记 , 则( )A、 B、 C、的最小值为 D、的最小值为11. 已知正数 ,满足 ,则( )A、 B、 C、 D、12. 已知函数 , 以下结论中正确的是( )A、是偶函数 B、有无数个零点 C、的最小值为 D、的最大值为1
三、填空题
-
13. 已知随机变量 , 则.14. 写出一个同时具有下列性质①②的函数.
①;②.
15. 若实数 , 满足 ,则 的最小值为.16. 倡导环保意识、生态意识,构建全社会共同参与的环境治理体系,让生态环保思想成为社会生活中的主流文化.为使排放的废气中含有的污染物量减少,某化工企业探索改良工艺,已知改良前所排放的废气中含有的污染物量为 , 首次改良后所排放的废气中含有的污染物量为.设改良前所排放的废气中含有的污染物量为(单位:),首次改良后所排放的废气中含有的污染物量为(单位:),则第n次改良后所排放的废气中的污染物量(单位:)满足函数模型.(1)、;(2)、依据当地环保要求,企业所排放的废气中含有的污染物量不能超过 , 则至少进行次改良才能使该企业所排放的废气中含有的污染物量达标.(参考数据:)四、解答题
-
17. 已知 , 设.(1)、若“”是“”的充分不必要条件,求实数a的取值范围;(2)、若“”是“”的必要不充分条件,求实数a的取值范围.18. 已知 是定义在 上的奇函数,且 ,若 ,且 时,有 恒成立.
(Ⅰ)用定义证明函数 在 上是增函数;
(Ⅱ)解不等式: ;
(Ⅲ)若 对所有 恒成立,求实数m的取值范围.
19. 某校为了解高三学生周末在家学习情况,随机抽取高三年级甲、乙两班学生进行网络问卷调查,统计了甲、乙两班各40人每天的学习时间(单位:小时),并将样本数据分成 , , , , 五组,整理得到如下频率分布直方图:

参考公式: , .
参考数据①:
0.050
0.010
0.001
3.841
6.635
10.828
②若 ,则 , .
(1)、将学习时间不少于6小时和少于6小时的学生数填入下面的 列联表:不少于6小时
少于6小时
总计
甲班
乙班
总计
能以95%的把握认为学习时间不少于6小时与班级有关吗?为什么?
(2)、此次问卷调查甲班学生的学习时间大致满足 ,其中 等于甲班学生学习时间的平均数,求甲班学生学习时间在区间 的概率.