浙江省杭州西湖区2022-2023学年七年级上学期新生素质抽测调研分班考数学试题
试卷更新日期：2022-08-26 类型：开学考试
一、选择题：本大题有10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的。
-
1. 下列图标是轴对称图形的是（ ）A、
B、
C、
D、
2. 11个相同的球放进4个不同的盒子，在不同的放法里，总有一个盒子至少放了（ ）个球A、1 B、2 C、3 D、43. 2022年2月5日，杭州某区最高气温7℃，最低气温为-2℃，那么这天的最高气温比最低气温高（ ）A、5℃ B、9℃ C、-5℃ D、-9℃4. 一副三角板如图放置，则∠ABC的度数是（ ）
A、135° B、120° C、105° D、75°5. 如果用●代表间一个自然数（●≠0），那么下面各式中，得数最大的是（ ）A、●÷ B、÷● C、●× D、●-6. 吸烟不仅有害健康还很花钱，如果一位吸烟者平均每天吸一包价值29元的烟，那么，他每年花在吸烟上的钱大约要（ ）元A、9000 B、11000 C、13000 D、150007. 一个不透明的袋子中装有9个球，其中有2个红球、3个黄球和4个白球，这些球除颜色外无其他差别，从袋子中随机取出1个球，设取出的是红球的可能性是a，取出的是黄球的可能性是b，取出的是白球的可能性是c，比较可能性的大小为（ ）A、a>b>c B、b>c>a C、c>a>b D、c>b>a8. 要剪一个面积是12.56平方厘米的圆形纸片，至少需要面积是（ ）平方厘米的正方形纸片（π取3.14）.A、12.56 B、14 C、16 D、209. 观察下表，当x=7时，则y的值为（ ）x
1
2
3
4
……
y
120
125
130
135
……
A、140 B、145 C、150 D、15510. 有三个两位数a，b，c，其中a是质数，b是能被5整除的偶数、c是6的倍数，并且满足80<a<b<c<100。学习小组的同学对其进行研究后得出结论：小敏说“满足条件的整数a只有一个”，小杰说“满足条件的整数b只有一个，小安说“a除以b一定大于b除以c”，下列结论中正确的是（ ）A、只有小敏是对的 B、小杰和小安是对的 C、只有小安是错的 D、小敏和小安是铅的二、填空题：本大题有6个小题，每小题4分，共24分
-
11. 比大小：19.1918.20（填“>”或“<"）．12. 七年级（2）班全体问学在“支援灾区献爱心”活动中都捐了款，具体情况如下：捐款10元2人，20元24人，30元21人，40元3人，则该班学生平均每人捐款元．13. 某商店把一种商品按标价的八折出售，每件获利是进价的20%，而该商品每件的进价为80元，则该商品的标价是元。14. 如图，硬纸片沿虛线折起来便可成一个正方体，与3号面相对的是号面。
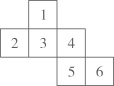15. 学校仪仗队进行队列训练，每5人站成一排或每4人站成一排都多2人。仪仗队至少有名学生。16. 一个底面半径是10cm的圆柱形水箱水深15cm，放入一个半径是8cm，高为6cm的圆锥，圆锥完全没入水中（水未溢出），此时的水深为cm三、解答题：本大题有5个小题，共46分．解答应写出文字说明、证明过程或演算步骤．
-
17. 计算：(1)、0.75-(2)、6×（）18. 如图1表示的是某书店今年1~5月各月的营业总额情况，图2表示的是该书店“党史"类书籍的各月营业额占书店当月营业总额的百分比情况。若该书店1~5月的营业总额一共是182万元，观察图1、图2，解答下列问题：
(1)、求该书店4月份的营业总额，并补全条形统计图。(2)、求5月份“党史”类书籍的营业额。(3)、请你判断这5个月中哪个月“党史”类书籍的营业额最高，并说明理由。19. 如图，已知梯形ABCD，点A，B，C，D的位置用数对表示分别是（1，5），（2，3），（3，3），（3，5）。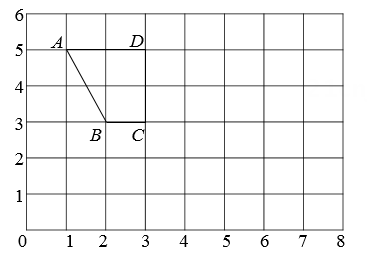
(1)、画出梯形ABCD向下平移3格后的图形，平移后点D对应点D的位置用数对表示是（ ， ）。(2)、在方格中选一空白处，画一个面积与梯形ABCD的面积相等的三角形（三角形的顶点为格点）。20. 甲乙两车从A地开往B地，在同一条公路上行驶，情况如图所示。
(1)、甲车先慢后快，它的平均速度是每小时多少千米？(2)、根据乙车的行车轨迹，可以知道哪两种量存在怎样的比例关系？为什么？21. 如图，学校有一块足够大的空地，其中有一段长为10米的墙MN，现准备用24米的篱笆围成长方形花圃ABCD（靠墙一边不用围篱笆），数学社团的同学设计如图1和如图2的两种方案（图1中AD的长等于墙长，图2中AD长不超过墙长）。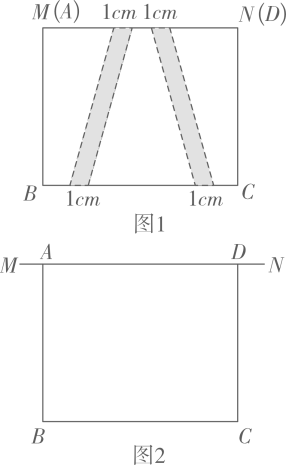
(1)、方案一：花圃中修建两条宽为1米的小路（小路两旁无篱笆），求此时长方形花圃ABCD（含小路）的面积．(2)、方案二：利用黄金分割知识（如果长方形宽与长的比值接近0.6，可以增加视觉的美感，即=0.6）社长说：“此方案有问题，不可行”。请你通过计算，说明不可行的理由。