山东省枣庄市滕州市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
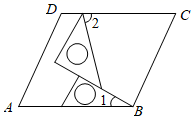
1. 下列等式从左到右变形,属于因式分解的是( )A、(a+b)(a﹣b)=a2﹣b2 B、x2﹣2x+1=(x﹣1)2 C、2a﹣1=a(2﹣) D、x2+6x+8=x(x+6)+82. 下列不能判断一个四边形是平行四边形的是( )A、一组对边平行且相等的四边形 B、两组对边分别相等的四边形 C、对角线互相平分的四边形 D、一组对边相等,且另一组对边平行的四边形3. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )
 A、 B、 C、 D、4. 如图,将△ABC绕点A逆时针旋转55°,得到△ADE,若∠E=65°,且AD⊥BC于点F,则∠BAC的度数为( )
A、 B、 C、 D、4. 如图,将△ABC绕点A逆时针旋转55°,得到△ADE,若∠E=65°,且AD⊥BC于点F,则∠BAC的度数为( ) A、65° B、70° C、75° D、80°5. 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
A、65° B、70° C、75° D、80°5. 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( ) A、140 B、70 C、35 D、246. 若关于x的分式方程 有增根,则m的值是( )A、1 B、﹣1 C、2 D、﹣27. 已知 ,则分式 与 的大小关系是( )A、 B、 C、 D、不能确定8. 如图,一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水,将瓶盖盖好后倒置,墨水水面高为h厘米,则瓶内的墨水的体积约占玻璃瓶容积的( )
A、140 B、70 C、35 D、246. 若关于x的分式方程 有增根,则m的值是( )A、1 B、﹣1 C、2 D、﹣27. 已知 ,则分式 与 的大小关系是( )A、 B、 C、 D、不能确定8. 如图,一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水,将瓶盖盖好后倒置,墨水水面高为h厘米,则瓶内的墨水的体积约占玻璃瓶容积的( )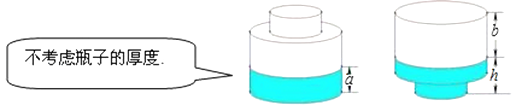 A、 B、 C、 D、9. 如图,▱ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是( )
A、 B、 C、 D、9. 如图,▱ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是( ) A、10 B、8 C、7 D、610. 甲、乙两人沿着总长度为的“健身步道”健步走,甲的速度是乙的1.2倍,甲比乙提前12分钟走完全程.设乙的速度为 , 则下列方程中正确的是( )A、 B、 C、 D、11. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )
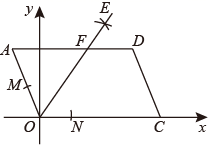
A、10 B、8 C、7 D、610. 甲、乙两人沿着总长度为的“健身步道”健步走,甲的速度是乙的1.2倍,甲比乙提前12分钟走完全程.设乙的速度为 , 则下列方程中正确的是( )A、 B、 C、 D、11. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )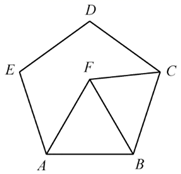 A、 B、 C、 D、12. 已知: 的顶点 ,点C在x轴的正半轴上,按以下步骤作图:
A、 B、 C、 D、12. 已知: 的顶点 ,点C在x轴的正半轴上,按以下步骤作图:①以点O为圆心,适当长为半径画弧,分别交 于点M , 交 于点N . ②分别以点M , N为圆心,大于 的长为半径画弧,两弧在 内相交于点E . ③画射线 ,交 于点 ,则点A的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式: .14. 若关于x的不等式组的解集为3≤x≤4,则a+b的值为 .15. 若关于x的分式方程 的解是正数,则k的取值范围是.16. 如图,在Rt△ABC中,∠C=90°,DE是线段AB的垂直平分线,已知 , 则∠A= .
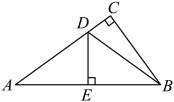 17. 对于实数a、b,定义一种新运算“※”为: , 例如: . 则方程的解是 .18. 如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值是 .
17. 对于实数a、b,定义一种新运算“※”为: , 例如: . 则方程的解是 .18. 如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值是 .
三、解答题
-
19. 解不等式组并把解集在数轴上表示出来.20. 先化简 , 然后从﹣1,0,3中选一个合适的数作为a的值代入求值.21. 如图,在5×5的方格纸中,△ABC的三个顶点都在格点上.
 (1)、将图1中的△ABC向下平移2格,画出平移后的△A1B1C1;(2)、将图2中的△ABC绕着点B按顺时针方向旋转90°,画出旋转后的△A2B2C2 .22. 先阅读下面的材料,然后回答问题:
(1)、将图1中的△ABC向下平移2格,画出平移后的△A1B1C1;(2)、将图2中的△ABC绕着点B按顺时针方向旋转90°,画出旋转后的△A2B2C2 .22. 先阅读下面的材料,然后回答问题:方程的解为 , ;
方程的解为 , ;
方程的解为 , ;…
(1)、观察上述方程的解,猜想关于x的方程的解是;(2)、根据上面的规律,猜想关于x的方程的解是 .(3)、根据上述规律,解关于y的方程 .23. 如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且 .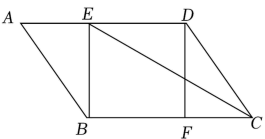 (1)、求证:四边形BEDF是平行四边形;(2)、连接CE,若CE平分∠DCB, , , 求平行四边形ABCD的周长.24. 实验学校购买A,B两种奖品,用于表彰在名著大阅读活动中表现突出的学生.已知A奖品比B奖品每件多25元,预算资金为1700元,其中800元购买了A奖品,其余资金购买了B奖品,且购买B奖品的数量是A奖品的3倍.(1)、求A,B奖品的单价;(2)、购买当日,正逢商店搞促销活动,所有商品均按原价八折销售,故学校调整了购买方案:不超过预算资金且购买A奖品的资金不少于720元,A,B两种奖品共100件,求购买A,B两种奖品的数量,有哪几种方案?25. 如图,在△ABC中,BC=24cm,射线AG∥BC,点E从点A出发沿射线AG以4cm/s的速度运动,当点E出发2s时,点F从点B出发沿射线BC以8cm/s的速度运动.设点F运动的时间为ts,其中t>0.连接AF,CE.
(1)、求证:四边形BEDF是平行四边形;(2)、连接CE,若CE平分∠DCB, , , 求平行四边形ABCD的周长.24. 实验学校购买A,B两种奖品,用于表彰在名著大阅读活动中表现突出的学生.已知A奖品比B奖品每件多25元,预算资金为1700元,其中800元购买了A奖品,其余资金购买了B奖品,且购买B奖品的数量是A奖品的3倍.(1)、求A,B奖品的单价;(2)、购买当日,正逢商店搞促销活动,所有商品均按原价八折销售,故学校调整了购买方案:不超过预算资金且购买A奖品的资金不少于720元,A,B两种奖品共100件,求购买A,B两种奖品的数量,有哪几种方案?25. 如图,在△ABC中,BC=24cm,射线AG∥BC,点E从点A出发沿射线AG以4cm/s的速度运动,当点E出发2s时,点F从点B出发沿射线BC以8cm/s的速度运动.设点F运动的时间为ts,其中t>0.连接AF,CE. (1)、当t=时,四边形ABFE是平行四边形;(2)、当t为何值时,以A,E,C,F为顶点的四边形是平行四边形;(3)、当t为何值时,S△ACE=2S△ACF.
(1)、当t=时,四边形ABFE是平行四边形;(2)、当t为何值时,以A,E,C,F为顶点的四边形是平行四边形;(3)、当t为何值时,S△ACE=2S△ACF.