山东省泰安市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 已知 ,则 的值为( ).A、 B、 C、 D、2. 下列各组二次根式,是同类二次根式的是( )A、与 B、与 C、与 D、与3. 如图,直线 , 直线AC分别交 , , 于点A,B,C;直线DF分别交 , , 于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
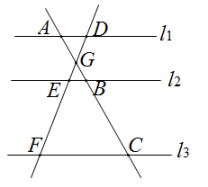 A、
A、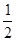 B、2
C、
B、2
C、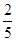 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 已知∽ , 和是它们的对应角平分线,若 , , 则与的面积比是( )A、: B、: C、: D、;6. 如图,点P在的边AC上,下列条件中不能判断的是( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 已知∽ , 和是它们的对应角平分线,若 , , 则与的面积比是( )A、: B、: C、: D、;6. 如图,点P在的边AC上,下列条件中不能判断的是( ) A、 B、 C、 D、7. 如图,在▱ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A、 B、 C、 D、7. 如图,在▱ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( ) A、1个 B、2个 C、3个 D、4个8. 如图,菱形ABCD的对角线AC与BD交于点O,过点C作AB垂线交AB延长线于点E,连结OE,若AB=2 , BD=4,则OE的长为( )
A、1个 B、2个 C、3个 D、4个8. 如图,菱形ABCD的对角线AC与BD交于点O,过点C作AB垂线交AB延长线于点E,连结OE,若AB=2 , BD=4,则OE的长为( ) A、6 B、5 C、2 D、49. 如图,△ABC与△DEF是位似图形,且位似中心为O,OB:OE=2:3,若△ABC的面积为4,则△DEF的面积为( )
A、6 B、5 C、2 D、49. 如图,△ABC与△DEF是位似图形,且位似中心为O,OB:OE=2:3,若△ABC的面积为4,则△DEF的面积为( ) A、2 B、6 C、8 D、910. 《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲、乙行各几何.”大意是说:已知甲、乙两人同时从同一地点出发,甲的速度为7,乙的速度为3,乙一直向东走,甲先向南走10步,后又向东北方向走了一段后与乙相遇,那么相遇时所用时间为多少?若设甲与乙相遇时间为x,则可列方程为( )A、 B、 C、 D、11. 如图, , , , D为上一点,且 , 在上取一点E,使以A、D、E为顶点的三角形与相似,则等于( )
A、2 B、6 C、8 D、910. 《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲、乙行各几何.”大意是说:已知甲、乙两人同时从同一地点出发,甲的速度为7,乙的速度为3,乙一直向东走,甲先向南走10步,后又向东北方向走了一段后与乙相遇,那么相遇时所用时间为多少?若设甲与乙相遇时间为x,则可列方程为( )A、 B、 C、 D、11. 如图, , , , D为上一点,且 , 在上取一点E,使以A、D、E为顶点的三角形与相似,则等于( )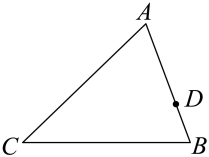 A、或 B、10或 C、或10 D、以上答案都不对12. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
A、或 B、10或 C、或10 D、以上答案都不对12. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④ .
其中正确结论的个数是( )
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 使代数式 有意义的x的取值范围是 .14. 若关于x的一元二次方程(a是常数)有实根,那么a的取值范围是 .15. 如图,乐器上的一根弦 , 两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点(即是与的比例中项),支撑点D是靠近点A的黄金分割点,则 . (结果保留根号)
 16. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,若∠E=20°,则∠ADB=.
16. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,若∠E=20°,则∠ADB=. 17. 市政府为了解决市民看病难的问题,决定下调药品的价格.某种药品经过连续两次降价后,由每盒300元下调至192元,则这种药品平均每次降价的百分率为 .18. 如图,正方形城邑的四面正中各有城门,出北门20步的A处(步)有一树木,由南门14步到C处(步),再向西行1775步到B处(步),正好看到A处的树木(点D在直线上),则城邑的边长为步.
17. 市政府为了解决市民看病难的问题,决定下调药品的价格.某种药品经过连续两次降价后,由每盒300元下调至192元,则这种药品平均每次降价的百分率为 .18. 如图,正方形城邑的四面正中各有城门,出北门20步的A处(步)有一树木,由南门14步到C处(步),再向西行1775步到B处(步),正好看到A处的树木(点D在直线上),则城邑的边长为步.
三、解答题
-
19. 计算:(1)、;(2)、20. 按照指定方法解下列方程:(1)、(公式法);(2)、(配方法);(3)、(因式分解法).21. 如图,正方形和正方形有公共点A,点B在线段上.判断与的位置关系,并说明理由;
 22. 如图,操场边的路灯照在水平放置的单杠上,在地面上留下影子 , 经测量得知米,米,单杠高1.6米,试求路灯P的高度.
22. 如图,操场边的路灯照在水平放置的单杠上,在地面上留下影子 , 经测量得知米,米,单杠高1.6米,试求路灯P的高度. 23. 如图,中, , 过点B作的平行线,与的平分线交于点D,点E是上一点,于点F,连接 .
23. 如图,中, , 过点B作的平行线,与的平分线交于点D,点E是上一点,于点F,连接 . (1)、求证:四边形是菱形;(2)、若 , , 求的长.
(1)、求证:四边形是菱形;(2)、若 , , 求的长.
