山东省聊城市冠县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个数中，无理数是（）

A、－ $\sqrt{4}$ B、 $\frac{2}{3}$ C、－π D、0.363363336

查看试题解析
2. 下列各图是选自历届冬奥会会徽中的图案，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若代数式 $\sqrt{1 + x^{2}}$ 有意义，则x必须满足条件（）

A、 $x \geq 0$ B、 $x > - 1$ C、 $x \geq - 1$ D、 $x$ 为任意实数

查看试题解析
4. 如图，在△ABC中，点D、E分别是AB、AC的中点，若∠B=40°，则∠BDE的度数为（）

A、40° B、50° C、140° D、150°

查看试题解析
5. 如图所示，一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $P (3 ， 2)$ ，则方程 $k x + b = 2$ 的解是（）

A、 $x = 1$ B、 $x = 2$ C、 $x = 3$ D、无法确定

查看试题解析
6. 有三个实数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 满足 $a_{1} - a_{2} = a_{2} - a_{3} > 0$ ，若 $a_{1} + a_{3} = 0$ ，则下列判断中正确的是（）

A、 $a_{1} < 0$ B、 $a_{2} > 0$ C、 $a_{1} + a_{2} < 0$ D、 $a_{2} \cdot a_{3} = 0$

查看试题解析
7. 如图，数轴A、B两点分别对应实数a、b，则下列结论正确的是（）

A、 $a + b > 0$ B、 $a b > 0$ C、 $\frac{1}{a} - \frac{1}{b} < 0$ D、 $\frac{1}{a} + \frac{1}{b} > 0$

查看试题解析
8. 当 $x > 2$ 时， $\sqrt{{(2 - x)}^{2}}$ = （）

A、 $2 - x$ B、 $x - 2$ C、 $2 + x$ D、 $\pm (x - 2)$

查看试题解析
9. 如图，在△ABC中，AB＝5，BC＝8， $∠ B = 6 0^{∘}$ ，将△ABC绕点A顺时针旋转得到△ADE，当点B的对应点D恰好落在BC边上时，CD的长为（）

A、3 B、4 C、5 D、6

查看试题解析
10. 已知关于x的不等式组 ${\begin{array}{l} x - a \geq 0 \\ 3 - 2 x > 0 \end{array}$ 的整数解共有4个，则a的取值范围是（）

A、 $- 3 \leq a < - 2$ B、 $- 3 < a \leq - 2$ C、 $- 3 < a < - 2$ D、 $a < - 2$

查看试题解析
11. 如图，正方形ABCD中，点F为AB上一点，CF与BD交于点E，连接AE，若∠BCF=20°，则∠AEF的度数（）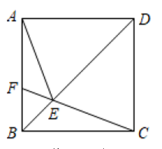

A、35° B、40° C、45° D、50°

查看试题解析
12. 如图，在平面直角坐标系中，已知点 $M_{0}$ 的坐标为 $(1 ， 0)$ ，将线段 $O M_{0}$ 绕原点О逆时针方向旋转45°，再将其延长到 $M_{1}$ ，使得 $M_{1} M_{0} ⊥ O M_{0}$ ，得到线段 $O M_{1}$ ；又将线段 $O M_{1}$ 绕原点O逆时针方向旋转45°，再将其延长到 $M_{2}$ ，使得 $M_{2} M_{1} ⊥ O M_{1}$ ，得到线段 $O M_{2}$ ；如此下去，得到线段 $O M_{3}$ ， $O M_{4}$ ， $O M_{5}$ ， …根据以上规律，则点 $M_{2022}$ 的坐标为（）

A、 $(2^{1011} ， 0)$ B、 $(0 ， - 2^{2022})$ C、 $(0 ， - 2^{1011})$ D、 $(- {(\sqrt{2})}^{2021} ， - {(\sqrt{2})}^{2021})$

查看试题解析

二、填空题

13. 点A(5，-3)向左平移3个单位，再向下平移2个单位后的坐标是

查看试题解析
14. 某学校生物课把学生的笔试、实验操作两项成绩分别按60％、40％的比例计入学生的学期总成绩，小亮的实验操作这一项成绩是81分，要想学期总成绩不低于90分，那么他的笔试成绩至少要达到分

查看试题解析
15. 如图，菱形 $A B C D$ 的边长为4， $∠ D A B = 60 °$ ，对角线 $A C$ ， $B D$ 相交于点O，点E，F同时从O点出发在线段 $A C$ 上以 $0.5 c m / s$ 的速度反向运动（点E，F分别到达A，C两点时停止运动），设运动时间为 $t s$ ．连接 $D E$ ， $D F$ ， $B E$ ， $B F$ ，当t=s时，四边 $D E B F$ 为正方形．

查看试题解析
16. 某快递公司每天上午7：00-8：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，下列说法：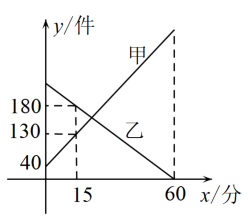
①15分钟后，甲仓库内快件数量为180件；
②乙仓库每分钟派送快件数量为4件；
③8：00时，甲仓库内快件数为600件；
④7：20时，两仓库快递件数相同．
其中正确的个数为．

查看试题解析
17. 如图，在正方形ABCD中，点E，F分别在边BC、CD上，连接AE，BF.若AB $= \sqrt{15}$ ，BE＝DF，则AE+BF的最小值为 .

查看试题解析

三、解答题

18. 计算：

(1)、 $\frac{\sqrt{20} + \sqrt{5}}{\sqrt{5}} - \sqrt[3]{27}$ ；

(2)、 $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})$ ．

查看试题解析
19. 解不等式（组）：

(1)、 $\frac{3 - 2 x}{3} \geq 2$ ；

(2)、 ${\begin{array}{l} 2 (2 x - 1) > 2 x - 1 \\ \frac{2 - 3 x}{4} < \frac{3 x - 2}{2} \end{array}$ ．

查看试题解析
20. 如图，一高层住宅发生火灾，消防车立即赶到距大厦12米（ $A C$ 的长）处，升起云梯到火灾窗口，云梯 $A B$ 长20米，云梯底部距地面3米（ $A E$ 的长），问：发生火灾的住户窗口距离地面有多高（ $B D$ 的长）？

查看试题解析
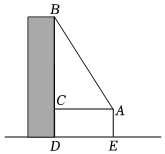21. 如图，直线 $y = 3 x + 4$ 与x轴相交于点A，与y轴相交于点B．

(1)、求A，B两点的坐标；

(2)、过B点作直线与x轴交于点P，若△ABP的面积为5，试求点P的坐标．

查看试题解析
22. 如图，在矩形ABCD中，对角线AC，BD相交于点O，DE∥AC，CE∥BD．

(1)、求证：四边形ODEC为菱形；

(2)、连接OE，若BC＝2 $\sqrt{2}$ ，求OE的长．

查看试题解析
23. 如图，在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为A（1，－4），B（5，－4），C（4，－1）．
( 1 )画出 $△ A B C$ 关于原点O成中心对称的 $△ A_{1} B_{1} C_{1}$ ；
( 2 )画出 $△ A_{1} B_{1} C_{1}$ 绕点O逆时针旋转90°所得到的 $△ A_{2} B_{2} C_{2}$ ，并写出 $C_{2}$ 的坐标；
( 3 )将 $△ A B C$ 先向右平移2个单位长度，再向上平移6个单位长度，画出第二次平移后的 $△ A_{3} B_{3} C_{3}$ ，并写出 $C_{3}$ 的坐标．

查看试题解析
24. 我们规定用 $(a ， b)$ 表示一对数对，给出如下定义：记 $m = \frac{1}{\sqrt{a}}$ ， $n = \sqrt{b}$ （ $a > 0$ ， $b > 0$ ），将 $(m ， n)$ 与 $(n ， m)$ 称为数对 $(a ， b)$ 的一对“对称数对”．例如： $(4 ， 1)$ 的一对“对称数对”为 $(\frac{1}{2} ， 1)$ 与 $(1 ， \frac{1}{2})$ ．

(1)、求数对 $(25 ， 4)$ 的一对“对称数对”；

(2)、若数对 $(3 ， y)$ 的一对“对称数对”的两个数对相同，求y的值；

(3)、若数对 $(a ， b)$ 的一对“对称数对”的一个数对是 $(3 ， 3 \sqrt{3})$ ，求 $a b$ 的值．

查看试题解析
25. 冰墩墩（Bing Dwen Dwen），是2022年北京冬季奥运会的吉祥物．将熊猫形象与富有超能量的冰晶外壳相结合，头部外壳造型取自冰雪运动头盔，装饰彩色光环，整体形象酷似航天员．冬奥会来临之际，冰墩墩玩偶非常畅销．小冬在某网店选中A，B两款冰墩墩玩偶，决定从该网店进货并销售．两款玩偶的进货价和销售价如表：
价格
类别
A款玩偶
B款玩偶
进货价（元/个）
20
15
销售价（元/个）
28
20

(1)、第一次小冬550元购进了A，B两款玩偶共30个，求两款玩偶各购进多少个．

(2)、第二次小冬进货时，网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半．小冬计划购进两款玩偶共30个，应如何设计进货方案才能获得最大利润，最大利润是多少？

(3)、小冬第二次进货时采取了（2）中设计的方案，并且两次购进的玩偶全部售出，请从利润率的角度分析，对于小冬来说哪一次更合算？（注：利润率=（利润÷成本）×100%）．

查看试题解析