山东省济宁市微山县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 下列式子没有意义的是( )A、 B、 C、 D、2. 在▱ABCD中,∠A=50°,则∠C=( )A、130° B、50° C、40° D、25°3. 下列计算结果正确的是( )A、=3 B、3﹣=3 C、÷=2 D、+=4. 某公司招聘大堂经理,考核项目为个人形象、交际能力、专业知识三个项目,并按2:4:4的权重计算出个人最终得分.某应聘者三项得分依次为80,85,90,则他的最终得分是( )A、85 B、86 C、87 D、885. 已知函数y=(m﹣3)+4是关于x的一次函数,则m的值是( )A、m=±3 B、m≠3 C、m=3 D、m=﹣36. 如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池边,它的顶端恰好到达池边的水面,求水的深度是( )尺
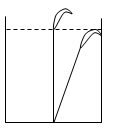 A、8 B、10 C、13 D、127. 若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )A、
A、8 B、10 C、13 D、127. 若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )A、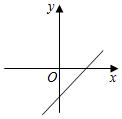 B、
B、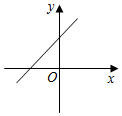 C、
C、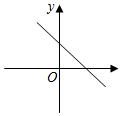 D、
D、 8. 如图,菱形ABCD的对角线相交于点O,E是CD的中点,且OE=3,则菱形的周长是( )
8. 如图,菱形ABCD的对角线相交于点O,E是CD的中点,且OE=3,则菱形的周长是( )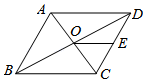 A、12 B、16 C、20 D、249. 如图,直线 与 的交点的横坐标为 ,则关于 的不等式 的整数解为( ).
A、12 B、16 C、20 D、249. 如图,直线 与 的交点的横坐标为 ,则关于 的不等式 的整数解为( ).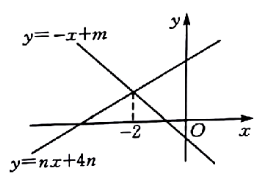 A、 B、 C、 D、10. 如图,A,B两地之间的路程为4500m,甲、乙两人骑车都从A地出发,已知甲先出发6min后,乙才出发,乙在A,B之间的C地追赶上甲,当乙追赶上甲后,乙立即返回A地,甲继续往B地前行.甲到达B地后停止骑行,乙骑行到达A地时也停止(乙在C地掉头时间忽略不计),在整个骑行过程中,甲和乙都保持各自速度匀速骑行,甲、乙两人相距的路程y(m)与甲出发的时间x(min)之间的关系如图所示,则下列说法正确的是( )
A、 B、 C、 D、10. 如图,A,B两地之间的路程为4500m,甲、乙两人骑车都从A地出发,已知甲先出发6min后,乙才出发,乙在A,B之间的C地追赶上甲,当乙追赶上甲后,乙立即返回A地,甲继续往B地前行.甲到达B地后停止骑行,乙骑行到达A地时也停止(乙在C地掉头时间忽略不计),在整个骑行过程中,甲和乙都保持各自速度匀速骑行,甲、乙两人相距的路程y(m)与甲出发的时间x(min)之间的关系如图所示,则下列说法正确的是( )①甲的速度为150m/min;
②乙的速度为240m/min;
③图中M点的坐标为(24,3600);
④乙到达A地时,甲离B地还有1000m.
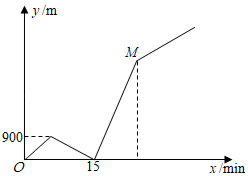 A、①② B、③④ C、②④ D、①③
A、①② B、③④ C、②④ D、①③二、填空题
-
11. 已知a<<b,若a,b是两个连续整数,则a+b的值是 .12. 已知直角三角形的两边长分别为3、4.则第三边长为.13. 已知点和点都在正比例函数的图象上.请你写出一个符合条件的k值 (写出一个即可),使当x1<x2时,y1>y2 .14. 已知数据a1 , a2 , a3 , a4的平均数是x,则2a1+1,2a2+1,2a3+1,2a4+1的平均数是 .15. 如图,▱ABCD中,∠ABC=120°,点E,F分别在AB,BC的延长线上,EF⊥AB于点E,FDAC,CE=1,则EF的长是 .
三、解答题
-
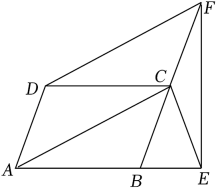
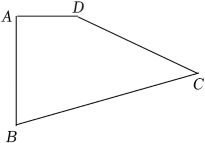
16. 计算:+(+1)(﹣1)﹣ .17. 如图,在四边形ABCD中,AD= , AB=5,BC=10,CD=8,∠BAD=90°,求四边形ABCD的面积.
 18. 某学校组织七、八年级全体学生举行了安全知识竞赛活动,为了解竞赛成绩情况,为两个年级各随机抽取10名学生的成绩(满分为100分)进行了分析,并依据分析结果绘制了如下表所示的不完整统计表:
18. 某学校组织七、八年级全体学生举行了安全知识竞赛活动,为了解竞赛成绩情况,为两个年级各随机抽取10名学生的成绩(满分为100分)进行了分析,并依据分析结果绘制了如下表所示的不完整统计表:七年级:90,95,95,80,85,90,80,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90.
年级
平均数
中位数
众数
方差
七年级
89
m
90
39
八年级
n
90
p
q
根据以上信息解答下面问题:
(1)、填空:m= , p= ;(2)、求q的值;(3)、通过数据分析,你认为哪个年级的成绩比较好?说明理由.19. 如图,在矩形ABCD中,对角线AC,BD交于点O,分别过点C,D作BD,AC的平行线交于点E,连接OE交CD于点F.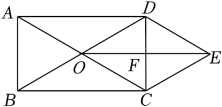 (1)、求证:四边形OCED是菱形;(2)、若AC=12,∠DOC=60°,求菱形OCED的面积.20. 某校计划租用甲、乙两种客车共7辆,载着八年级330名师生去参加社会实践活动,甲、乙两种客车的载客量和租金如下表.
(1)、求证:四边形OCED是菱形;(2)、若AC=12,∠DOC=60°,求菱形OCED的面积.20. 某校计划租用甲、乙两种客车共7辆,载着八年级330名师生去参加社会实践活动,甲、乙两种客车的载客量和租金如下表.客车型号
甲种
乙种
载客量(座/辆)
50
35
租金(元/辆)
550
400
(1)、设租用甲种客车x辆,租用甲、乙两种客车的总费用为y元,请写出y关于x的函数解析式;(2)、为确保所有的师生都能去参加社会实践活动,应租用甲种客车多少辆,才能使租用甲、乙两种客车总费用最少?最少费用是多少元?21. 下面我们参照学习函数的过程与方法,探究函数的图象与性质.(1)、请根据下表中所给x,y的对应值,以自变量x的取值为横坐标,以相应的函数y的值为纵坐标,在平面直角坐标系中(如图所示)画出函数图象:x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
0
1
2
3
2
1
0
1
2
…
 (2)、结合表格和图像,解回答下列问题:
(2)、结合表格和图像,解回答下列问题:①若点(﹣ , ),( , )在函数图象上,则 ▲ (填“>”,“=”或“<”);
②点A的坐标是(0,a),过点A作直线l垂直于y轴,当直线l与函数图象有三个不同交点时,直接写出a的取值范围;
③当y=5时,求x的值.
22. 如图,直线y=﹣x+5与y轴、x轴分别交于点A,B,以AB为边在第一象限内作正方形ABCD,E是x轴上一动点,设点E坐标为(m,0)(2<m<).连接AE交BD于点F,作直线CF与y轴相交于点G.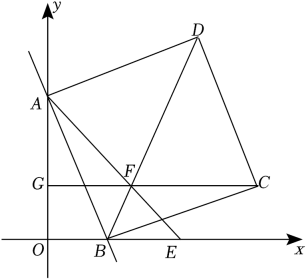 (1)、填空:点A的坐标是 , 点B的坐标是 , 点C的坐标是 , 点D的坐标是;(2)、求证:∠EAB=∠GCB;(3)、是否存在这样的m值,使GC⊥y轴?若存在,请求出此时的m值;若不存在,请说明理由.
(1)、填空:点A的坐标是 , 点B的坐标是 , 点C的坐标是 , 点D的坐标是;(2)、求证:∠EAB=∠GCB;(3)、是否存在这样的m值,使GC⊥y轴?若存在,请求出此时的m值;若不存在,请说明理由.