山东省济南市长清区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 若x＞y，则下列不等式成立的是（）

A、x＋5＞y＋5 B、 $\frac{1}{3}$ x＜ $\frac{1}{3}$ y C、－8x＞－8y D、x－10＞y＋10

查看试题解析
3. 下列各式由左边到右边的变形中，属于分解因式的是（）

A、 $a (x - y) = a x - a y$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 $x^{2} - 4 x + 3 = x (x - 4) + 3$ D、 $a^{2} + 1 = a (a + \frac{1}{a})$

查看试题解析
4. 把分式 $\frac{2 x y}{x + y}$ 到中的x、y都扩大3倍，则分式的值（）

A、不变 B、缩小为原来的 $\frac{1}{3}$ C、扩大6倍 D、扩大3倍

查看试题解析
5. 下面关于平行四边形的说法中，错误的是（　　）

A、对角线互相平分的四边形是平行四边形 B、有一组对边平行，另一组对边相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、有两组对角相等的四边形是平行四边形

查看试题解析
6. 已知关于x的一元二次方程 $m x^{2} + 2 x + 1 = 0$ 有两个不相等的实数根，则m的取值范围是（）

A、 $m \leq 1$ B、 $m < 1$ C、 $m \leq 1$ ，且 $m \neq 0$ D、 $m < 1$ ，且 $m \neq 0$

查看试题解析
7. 如图，在 ▱ ABCD中，点E为边BC的中点，对角线AC与BD相交于点O，且△ABC的周长为16，连接OE，则△OEC的周长为（）

A、5 B、5.5 C、6 D、8

查看试题解析
8. 若关于x的一元二次方程x²－2x＋m＝0有一个解为x＝－1，则另一个解为（）

A、3 B、1 C、－3 D、4

查看试题解析
9. 国家统计局统计数据显示，我国快递业务收入逐年增加。2017年至2019年我国快递业务收入由5000亿元增加到7500亿元，设我国2017年至2019年快递业务收入的年平均增长率为x，则可列方程为（）

A、500(1＋2x)＝7500 B、5000x2(1＋x)＝7500 C、5000(1＋x)²＝7500 D、5000＋5000(1＋x）＋5000(1＋x)²＝7500

查看试题解析
10. 关于x的分式方程 $\frac{x - 2}{x + 3} = 2 - \frac{a}{x + 3}$ 有增根，则a的值为（）

A、﹣3 B、﹣5 C、5 D、2

查看试题解析
11. 如图，在平面直角坐标系中，平行四边形OABC的顶点 $O (0 ， 0)$ ，点A在x轴的正半轴上，∠COA的平分线OD交BC于点 $D (2 ， 3)$ ，则点C的坐标为（）

A、 $(- \frac{5}{4} ， 3)$ B、 $(3 - \sqrt{13} ， 3)$ C、 $(- \frac{4}{5} ， 3)$ D、 $(2 - \sqrt{13} ， 3)$

查看试题解析
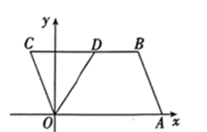12. 如图， ▱ ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°， $A B = \frac{1}{2} B C$ ，连接OE．下列结论：①∠ADO＝30°；②S _{▱ ABCD}＝AB·AC；③OB＝AB；④S_四_边_形OECD＝ $\frac{3}{2}$ S_△AOD ，其中成立的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

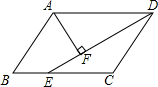
13. 分解因式：3ab－ac＝；

查看试题解析
14. 一个正多边形的每一个内角都是108°，则它是正边形.

查看试题解析
15. 在平面直角坐标系中，将点P先向左平移2个单位，再向下平移3个单位，得到的点坐标是（-3，1），则点P的坐标为．

查看试题解析
16. 如图，在平行四边形ABCD中，DE平分∠ADC交BC于E，AF⊥DE于F，已知∠DAF＝58°，则∠B＝．

查看试题解析
17. 如图，在一块长17m、宽12m的矩形空地上，修建两条同样宽的相互垂直的道路，剩余部分栽种花草，要使绿化面积为176m² ，则修建的路宽应为 m．

查看试题解析
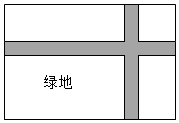18. 如图，在 $△$ ABC中， $∠ B A C = 60 °$ ， $∠ A B C = 45 °$ ， AD平分 $∠ B A C$ 交BC于点D，P为直线AB上一动点．连接DP，以DP、DB为邻边构造平行四边形DPQB，连接CQ，若 $A C = 6$ ．则CQ的最小值为．

查看试题解析

三、解答题

19. 因式分解：

(1)、a²－9；

(2)、2x²－12x＋18

查看试题解析
20. 解方程： $\frac{3 - x}{x - 4} + \frac{1}{4 - x} = 1$ ．

查看试题解析
21. 解不等式组： ${\begin{array}{l} 4 x - 8 \leq 0 \\ \frac{3 - x}{2} \geq 2 - x \end{array}$ 并写出所有的整数解．

查看试题解析
22. 先化简，再求值： $\frac{2 x + 2}{x^{2} - 4} ÷ (1 - \frac{x}{x + 2})$ ，其中 $x = 1$ .

查看试题解析
23. 如图，在平行四边形ABCD中，E、F是BC、AD上的两点，且AE∥CF．求证：BE＝DF．

查看试题解析
24. 如图，△ABC的中线BE，CF相交于点G，已知P，Q分别是BG，CG的中点．

(1)、求证：四边形EFPQ是平行四边形；

(2)、请判断BG与GE的数量关系，并证明．

查看试题解析
25. 冰墩墩是2022年北京冬奥会的吉祥物，其敦厚、可爱的形象深入人心，制作的奥运纪念品很受大家喜爱。已知A型号的冰墩墩手办比B型号的冰墩墩钥匙扣的单价多30元，用880元购买A型号手办的数量是用290元购买B型号钥匙扣数量的2倍．

(1)、求A，B两种型号纪念品的单价分别是多少元？

(2)、若计划购买A，B两种型号的纪念品共100个，且所花费用不超过6800元，求最多能购买多少个A型号的纪念品？

查看试题解析
26. △ABC中，∠B=90°，AB=9，BC=12，点p从点A开始延边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P．Q分别从A．B同时出发，当点Q运动到点C时，两点停止运动，问：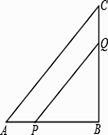

(1)、填空：BQ= ， PB=（用含t的代数式表示）

(2)、经过几秒，PQ的长为 $6 \sqrt{2}$ cm？

(3)、经过几秒， $Δ P B Q$ 的面积等于 $8 c m^{2}$ ?

查看试题解析
27. 如图，已知直线 $y = k x + b$ 经过 $A (6 ， 0)$ ， $B (0 ， 3)$ 两点．

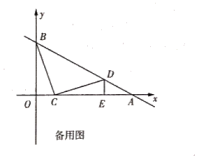(1)、求直线 $y = k x + b$ 的解析式；

(2)、若C是线段OA上一点，将线段CB绕点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上.
①求点C和点D的坐标；

②若点P在y轴上，Q在直线AB上，是否存在以C，D，P，Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点Q的坐标，否则说明理由．

查看试题解析