山东省济南市商河县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则下列不等式一定成立的是:( )A、 B、 C、 D、3. 下列从左边到右边的变形,属于因式分解的是( )A、(x+1)(x-1)=x2-1 B、x2-2x+1=x(x-2)+1 C、a(x-y)=ax-ay D、x2+2x+1=(x+1)24. 若分式有意义,则x的取值范围是( ).A、 B、 C、 D、5. 将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是( )A、(5,﹣1) B、(﹣1,﹣1) C、(﹣1,3) D、(5,3)6. 如图,在平行四边形ABCD中,∠B=60°,则∠D=( )
2. 若 , 则下列不等式一定成立的是:( )A、 B、 C、 D、3. 下列从左边到右边的变形,属于因式分解的是( )A、(x+1)(x-1)=x2-1 B、x2-2x+1=x(x-2)+1 C、a(x-y)=ax-ay D、x2+2x+1=(x+1)24. 若分式有意义,则x的取值范围是( ).A、 B、 C、 D、5. 将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是( )A、(5,﹣1) B、(﹣1,﹣1) C、(﹣1,3) D、(5,3)6. 如图,在平行四边形ABCD中,∠B=60°,则∠D=( ) A、60° B、120° C、140° D、30°7. 不等式组 的解集在数轴上表示正确的是( )A、
A、60° B、120° C、140° D、30°7. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、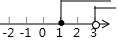 C、
C、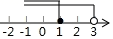 D、
D、 8. 计算 的结果是( )A、 B、 C、 D、9. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若PA=4,则PQ的最小值为( )
8. 计算 的结果是( )A、 B、 C、 D、9. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若PA=4,则PQ的最小值为( ) A、 B、2 C、4 D、10. 不能判定一个四边形是平行四边形的条件是()
A、 B、2 C、4 D、10. 不能判定一个四边形是平行四边形的条件是()
A、两组对边分别平行 B、一组对边平行,另一组对边相等 C、一组对边平行且相等 D、两组对边分别相等11. 如图,在中, , , 将绕点C按顺时针方向旋转后得到 , 此时点D在AB边上,则旋转角的大小为( ) A、20° B、40° C、70° D、50°12. 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A-45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为( )
A、20° B、40° C、70° D、50°12. 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A-45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为( ) A、 B、5 C、4 D、
A、 B、5 C、4 D、二、填空题
-
13. 分解因式: .14. 若分式 的值为0,则x的值是 .15. 如图,正方形AMNP的边AM在正五边形ABCDE的边AB上,则∠PAE= .
 16. 若不等式(m-2)x>1的解集是x< ,则m的取值范围是 .17. 如图,在平行四边形ABCD中,CE平分∠BCD,若DC=5,CB=3,则AE的长为 .
16. 若不等式(m-2)x>1的解集是x< ,则m的取值范围是 .17. 如图,在平行四边形ABCD中,CE平分∠BCD,若DC=5,CB=3,则AE的长为 . 18. 如图,点A的坐标为(1,3),点B在x轴上,把△OAB沿x轴向右平移到△ECD,若四边形ABDC的面积为15,则点C的坐标为 .
18. 如图,点A的坐标为(1,3),点B在x轴上,把△OAB沿x轴向右平移到△ECD,若四边形ABDC的面积为15,则点C的坐标为 .
三、解答题
-
19.(1)、解不等式, , 并把它的解集表示在数轴上.(2)、解不等式组: , 并写出不等式组的整数解.
 20. 把下列各式分解因式:(1)、4x2﹣16;(2)、2a2b﹣8ab+8b.21.(1)、计算:;(2)、先化简,再求值: , 其中x=2.22. 解方程: ﹣ =123. 如图,四边形ABCD是平行四边形,EF分别是BC、AD上的点,∠1=∠2.
20. 把下列各式分解因式:(1)、4x2﹣16;(2)、2a2b﹣8ab+8b.21.(1)、计算:;(2)、先化简,再求值: , 其中x=2.22. 解方程: ﹣ =123. 如图,四边形ABCD是平行四边形,EF分别是BC、AD上的点,∠1=∠2.求证:四边形AECF为平行四边形.
 24. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长1个单位长度的正方形).
24. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长1个单位长度的正方形).
( 1 )将△ABC沿x轴方向向左平移5个单位,画出平移后得到的△A1B1C1;直接写出点B1的坐标;
( 2 )将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;直接写出点B2的坐标;
( 3 )作出△ABC关于原点O成中心对称的△A3B3C3 , 并直接写出B3的坐标.
25. 2022年2月6日晚,中国女足在第20届亚洲杯决赛中以3:2逆转夺冠!全国各地掀起了一股学女足精神的热潮.某学校准备购买一批足球,第一次用3000元购进A类足球若干个,第二次又用3000元购进B类足球,购进数量比第一次多了20个.已知A类足球的单价是B类足球单价的1.5倍.(1)、求B类足球的单价是多少元;(2)、若学校需采购A,B两类足球共200个,总费用不超过12000元,则A类足球最多购买多少个?26. 如图,在△ABC 中,已知点 D 在线段 AB 的反向延长线上,过 AC的中点 F 作线段 GE 交∠DAC 的平分线于 E,交 BC 于 G,且 AE∥BC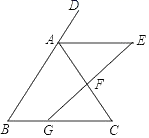 (1)、求证:△ABC 是等腰三角形;(2)、若 AE=8,AB=10,GC=2BG,求△ABC 的周长.27. 如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.
(1)、求证:△ABC 是等腰三角形;(2)、若 AE=8,AB=10,GC=2BG,求△ABC 的周长.27. 如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE. (1)、发现
(1)、发现①∠DCE的度数是;
②线段CA、CE、CD之间的数量关系是 .
(2)、探究如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.
(3)、拓展应用:如图3,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC的延长线上,连接CE,若AB=AC= , CD=1,求线段DE的长.