山东省济南市平阴县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 第24届冬奥会计划于2022年2月4日在北京开幕，北京将成为全球首个既举办过夏季奥运会又举办过冬季奥运会的城市.下列各届冬奥会会徽部分图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $m ＞ n$ ，下列不等式不一定成立的是（）

A、 $m + 3 ＞ n + 3$ B、 $﹣ 3 m ＜ ﹣ 3 n$ C、 $\frac{m}{3} > \frac{n}{3}$ D、 $m^{2} ＞ n^{2}$

查看试题解析
3. 下列分解因式正确的是（　　）

A、x²﹣4＝（x﹣4）（x+4） B、2x³﹣2xy²＝2x（x+y）（x﹣y） C、x²+y²＝（x+y）² D、x²﹣2x+1＝x（x﹣2）+1

查看试题解析
4. 下列各式：① $\frac{3}{x}$ ；② $\frac{x + y}{2}$ ；③ $\frac{a^{3}}{a}$ ；④ $\frac{x}{π - 1}$ ，其中是分式的是（）

A、①② B、③④ C、①③ D、①②③④

查看试题解析
5. 关于x的方程 $\frac{2 x - 1}{x - 2} = \frac{m}{x - 2} + 1$ 有增根，则m的值是（）

A、0 B、2或3 C、2 D、3

查看试题解析
6. 如果把 $\frac{5 x y}{x + y}$ 中的x和y都扩大为原来的10倍，那么这个分式的值（）

A、不变 B、扩大为原来的50倍 C、扩大为原来的10倍 D、缩小为原来的 $\frac{1}{10}$

查看试题解析
7. 一元二次方程 $x^{2} - 8 x - 1 = 0$ 配方后可变形为（）

A、 ${(x + 4)}^{2} = 17$ B、 ${(x + 4)}^{2} = 15$ C、 ${(x - 4)}^{2} = 17$ D、 ${(x - 4)}^{2} = 15$

查看试题解析
8. 如图，在四边形ABCD中，AB $∥$ CD，要使四边形ABCD是平行四边形，下列添加的条件错误的是（）

A、AB＝CD B、BC＝AD C、∠A＝∠C D、 $B C ∥ A D$

查看试题解析
9. 如图，在正五边形ABCDE中，连接BE，则∠ABE的度数为（）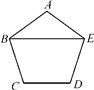

A、30° B、36° C、54° D、72°

查看试题解析
10. 如图，一个长为2、宽为1的长方形以下面的“姿态”从直线 $l$ 的左侧水平平移至右侧（下图中的虚线是水平线），其中，平移的距离是（）

A、1 B、2 C、3 D、 $2 \sqrt{2}$

查看试题解析
11. 若不等式组 ${\begin{array}{l} x < 1 \\ x < m \end{array}$ 的解为x＜m，则m的取值范围为（）

A、m≤1 B、m=1 C、m≥1 D、m＜1

查看试题解析
12. 如图，四边形ABCD中，AC＝a，BD＝b，且AC丄BD，顺次连接四边形ABCD 各边中点，得到四边形A₁B₁C₁D₁ ，再顺次连接四边形A₁B₁C₁D₁各边中点，得到四边形A₂B₂C₂D₂…，如此进行下去，得到四边形A_nB_nC_nD_n ．下列结论正确的个数有
① 四边形A₂B₂C₂D₂是矩形；
② 四边形A₄B₄C₄D₄是菱形；
③ 四边形A₅B₅C₅D₅的周长是 $\frac{a + b}{4}$ ；
④ 四边形A_nB_nC_nD_n的面积是 $\frac{a b}{2^{n + 1}}$ ．

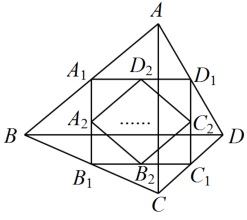A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分解因式：2m²－2n²＝；

查看试题解析
14. 点 $A (- 2 ， 3)$ 与点 $B (a ， b)$ 关于坐标原点对称，则a+b= ．

查看试题解析
15. 如图，在平面直角坐标系xOy中，若直线 $y_{1} = - 2 x + a$ ，直线 $y_{2} = b x - 4$ 相交于点 $P (1 ， - 3)$ ，则关于x的不等式 $- 2 x + a < b x - 4$ 的解集是.

查看试题解析
16. 若关于x的方程x²－2x＋m＝0有实数根，则m的取值范围为；

查看试题解析
17. 已知 $\frac{1}{x} - \frac{1}{y} = 3$ ，则代数式 $\frac{2 x + 7 x y - 2 y}{x - 2 x y - y}$ 的值为.

查看试题解析
18. 如图，在△ABC中，∠C＝90°，AC＝6，BC＝8，点D在AB边上，DE⊥AC，DF⊥BC，垂足分别为点E、F，连接EF，则线段EF的最小值等于.

查看试题解析

三、解答题

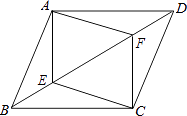
19. 计算

(1)、因式分解：x³y－6x²y＋9xy

(2)、解不等式组 ${\begin{array}{l} 3 x - (x - 3) \geq 1 \\ \frac{2 x + 1}{3} ＞ x - 1 \end{array}$

查看试题解析
20. 解方程

(1)、 $\frac{3}{x - 3}$ － $\frac{1}{x + 3}$ ＝ $\frac{18}{x^{2} - 9}$

(2)、x²－4x－12＝0．

查看试题解析
21. 先化简（1＋ $\frac{1}{x - 2}$ ）÷ $\frac{x^{2} - 2 x + 1}{x^{2} - 4}$ ，然后在－2，－1，0，1，2中选择一个合适的数代入求值．）

查看试题解析
22. 已知：如图，在▱ABCD中，E、F是对角线BD上的两点，且BE=DF，
求证：四边形AECF是平行四边形．

查看试题解析
23. 某单位计划从商店购买同一种品牌的钢笔和笔记本，已知购买一支钢笔比购买一个笔记本多用20元，若用1500元购买钢笔和用600元购买笔记本，则购买钢笔的数量是购买笔记本数量的一半，求购买一支钢笔、一个笔记本各需要多少元？

查看试题解析
24. 如图，△ABC三个顶点分别为A（1，1），B（4，2），C（3，4）．

(1)、请画出△ABC向左平移5个单位长度后得到的△A₁B₁C₁ ，此时B₁的坐标为；

(2)、请画出△A₁B₁C₁绕点A₁顺时针旋转90°的△A₂B₂C₂；并写出点B₂的坐标为；

(3)、在（1）的变换过程中线段CB扫过的面积为；

查看试题解析
25. 阅读材料：若m²－2mn＋2n²－8n＋16＝0，求m、n的值．
解：∵m²－2mn＋2n²－8n＋16＝0，
∴（m²－2mn＋n²）＋（n²－8n＋16）＝0，
∴（m－n）²＋（n－4）²＝0，
∴（m－n）²＝0，（n－4）²＝0，
∴n＝4，m＝4．
根据你的观察，探究下面的问题：

(1)、已知x²－2xy＋2y²＋6y＋9＝0，求 $x$ 、 $y$ 的值；

(2)、已知△АВС的三边长分别为а，b，с都是正整数，且满足a²＋b²－10a－12b＋61＝0，求△ABC的边a、b的值；

(3)、已知a－b＝8，ab＋c²－16c＋80＝0，求a＋b＋c的值．

查看试题解析
26.
在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．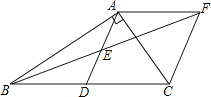

(1)、求证：△AEF≌△DEB

(2)、证明四边形ADCF是菱形。

(3)、若AC=4，AB=5，求菱形ADCF的面积．

查看试题解析
27. 如图，▱ABCD的对角线AC、BD相交于点O，AB⊥AC，AB＝3，∠ACB＝30°，点P从点A出发，沿AD以每秒1个单位的速度向终点D运动．连接PO并延长交BC于点Q．设点P的运动时间为t秒．

(1)、求证：AP＝CQ；

(2)、当四边形ABQP是平行四边形时，求t的值；

(3)、在P点运动过程中，当t为何值时，△AOP是等腰三角形．（直接写出答案即可）

查看试题解析