山东省济南市历下区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. “冰墩墩”将熊猫形象与富有超能量的冰晶外壳结合，体现了冬季冰雪运动与现代科技的特点．将如图所示的“冰墩墩”图案平移后可以得到（）

A、 B、 C、 D、

查看试题解析
2. 若 $a > b$ ，则下列式子中一定成立的是（）

A、 $- a < - b$ B、 $- \frac{a}{2} > - \frac{b}{2}$ C、 $a c > b c$ D、 $a - 2 < b - 2$

查看试题解析
3. 2022年4月16日，神舟十三号载人飞船返回舱在东风着陆场成功着陆．为迎接航天英雄，同学们设计了他们喜欢的航空飞行器的图案．其中，属于中心对称的图案设计是（）

A、 B、 C、 D、

查看试题解析
4. 下列分式中，属于最简分式的是（）

A、 $\frac{4}{2 a}$ B、 $\frac{y}{y^{2}}$ C、 $\frac{1 - m}{m - 1}$ D、 $\frac{x}{x + 3}$

查看试题解析
5. 要使分式 $\frac{x + 2}{x + 1}$ 有意义，x的取值应满足（）

A、 $x \neq - 1$ B、 $x \neq - 1$ 且 $x \neq - 2$ C、 $x \neq - 2$ D、 $x = - 1$

查看试题解析
6. 菲菲为了推理出七边形的内角和，将七边形的某一个顶点分别与其他各顶点相连，这样把原来的七边形分割成了（）个三角形，最终求出七边形内角和是900°．

A、4 B、5 C、6 D、7

查看试题解析
7. 矩形ABCD在平面直角坐标系中如图所示，若矩形平移，使得点A（-4，3）到点A′（1，4）的位置，平移后矩形顶点C的对应点C′的坐标是（）

A、 $C^{'} (- 2 ， 0)$ B、 $C^{'} (3 ， 0)$ C、 $C^{'} (3 ， 1)$ D、 $C^{'} (4 ， 1)$

查看试题解析
8. 下列各式中，能用公式法分解因式的是（）

A、 $x^{2} - x$ B、 $4 x^{2} + 4 x - 1$ C、 $x^{2} + y^{2}$ D、 $4 x^{2} - 1$

查看试题解析
9. 如图，将△ABC绕点C顺时针旋转35°得到△DEC，边ED，AC相交于点F，若∠A=30°，则∠AFD的度数为（）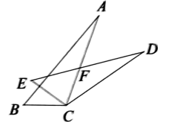

A、65° B、15° C、115° D、75°

查看试题解析
10. 某小区3000人进行核酸检测，由于组织有序，居民积极配合，实际每小时检测人数比原计划增加50人，结果提前2小时完成任务．若原计划每小时检测x人，可列方程（）

A、 $\frac{3000}{x} + 2 = \frac{3000}{x + 50}$ B、 $\frac{3000}{x + 50} - 50 = \frac{3000}{x}$ C、 $\frac{3000}{x + 50} + 50 = \frac{3000}{x}$ D、 $\frac{3000}{x} - 2 = \frac{3000}{x + 50}$

查看试题解析
11. 如图，在证明三角形的中位线定理时，小兰首先将原图形上面的三角形部分剪开，并旋转180°拼到下方．类似地，现有如图所示的四边形ABCD， $A D ∥ B C$ ，若 $A D = 3$ ， $B C = 7$ ， E、F分别是AB和DC的中点，则 $E F =$ （）

A、4 B、4.5 C、5 D、6

查看试题解析
12. 如图，在正方形ABCD外取一点E，连接AE，BE，DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB= $\sqrt{10}$ ，则点B到直线AE的距离是（）

A、 $\sqrt{2}$ B、2 C、 $\frac{5}{2}$ D、3

查看试题解析

二、填空题

13. 分解因式： $a^{2} - 4 a$ ＝．

查看试题解析
14. 如图，点C在 $∠ A O B$ 的平分线上， $C D ⊥ O A$ 于点D，且 $C D = 3$ ，如果E是射线OB上一点，那么线段CE长度的最小值是．

查看试题解析
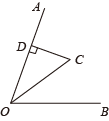15. 如图，在平行四边形ABCD中，AC、BD相交于点O， $∠ O D A = 90 °$ ， $A C = 10$ ， $B D = 6$ ，则BC的长为．

查看试题解析
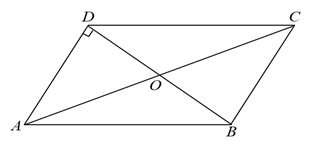16. 足球表面为什么用正六边形和正五边形构成？因为正六边形的两个内角和正五边形的一个内角加起来接近一个周角，而又不足一个周角．这样，由平面折叠而成的多面体充气后最终就呈现为球形．如图，在折叠前的平面上，拼接点处的缝隙∠AOB的大小为．

查看试题解析
17. 在冬奥会单板滑雪项目中，运动员的空中姿态优美飘逸．如图，在平面直角坐标系中，将我国运动员的初始位置用△ABC标记，则他在空中的运动可看成从初始位置绕某旋转中心逆时针旋转一定角度后到达另一位置，记为△A′B′C′，在这一过程中，旋转中心的坐标是．

查看试题解析
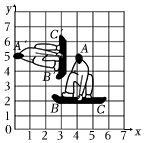18. 如图，在平行四边形ABCD中，E为CD中点，连接BE，F为BE中点，连接AF，若AB=8，BC=10，∠BAD=120°，则AF的长为．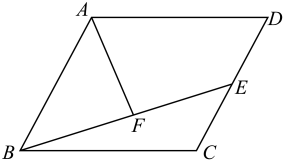

查看试题解析

三、解答题

19. 因式分解：

(1)、 $2 m^{2} - 18$ ；

(2)、 $a^{3} + 2 a^{2} + a$

查看试题解析
20. 解下列分式方程：

(1)、 $\frac{3 - x}{x - 4} + \frac{1}{4 - x} = 1$ ；

(2)、 $\frac{1}{x - 1} = \frac{1}{x^{2} - 1}$ ．

查看试题解析
21. 先化简，再求值： $x - 1 - \frac{x^{2}}{x + 1}$ ，其中 $x = 3$ ．

查看试题解析
22. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O．点E、F在对角线BD上，且BE=DF，连接AE、CF．求证：AE=CF．

查看试题解析
23. 如图，已知O是坐标原点，B、C两点的坐标分别为（3，-1），（2，1）

(1)、若 $△ B_{1} O C_{1}$ 与 $△ B O C$ 关于点O成中心对称，请直接写出对应点 $B_{1}$ 、 $C_{1}$ 的坐标；

(2)、将 $△ B O C$ 绕点O逆时针旋转90度，得到 $△ B_{2} O C_{2}$ ．请画出旋转后的 $△ B_{2} O C_{2}$ ．

查看试题解析
24. 列分式方程解应用题：
截止到2020年11月23日，全国832个国家级贫困县全部脱贫摘帽．某单位党支部在“精准扶贫”活动中，给结对帮扶的贫困家庭赠送甲､乙两种树苗．已知每棵乙种树苗的价格比甲种树苗的价格贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同，求甲､乙两种树苗每棵的价格．

查看试题解析
25. 如图，已知 $△ A B C$ 是等边三角形，E为AC上一点，连接BE．将 $△ B E C$ 旋转，使得点C落在BC上的点D处，点B落在BC上方的点F处，旋转后的三角形是 $△ F C D$ ，连接AF．请证明：四边形ABDF是平行四边形．

查看试题解析

26. 在小学，我们学习过能被3整除的数的规律，其实这个结论可以用因式分解的方法证明．

(1)、请你判断111222（填能或不能）被3整除；

(2)、为什么可以用各数位上的数字之和判断一个数能不能被3整除呢？小明先选了一个能被3整除的四位数“1236”试着进行推理：

$1236 = 1000 \times 1 + 100 \times 2 + 10 \times 3 + 1 \times 6$

$= (999 + 1) \times 1 + (99 + 1) \times 2 + (9 + 1) \times 3 + 6$

$= 999 \times 1 + 99 \times 2 + 9 \times 3 + (1 + 2 + 3 + 6)$

$= 3 (333 \times 1 + 33 \times 2 + 3 \times 3) + (1 + 2 + 3 + 6)$ ；

∵“ $3 (333 \times 1 + 33 \times 2 + 3 \times 3)$ ”能被3整除，

∴当“ $1 + 2 + 3 + 6$ ”被3整除，原数就能被3整除．

现在，设 $\bar{a b c d}$ 是个四位数，其个位、十位、百位、千位上的数字分别是d，c，b，a，请你借鉴小明的思路，证明：若“ $a + b + c + d$ ”能被3整除，则 $\bar{a b c d}$ 能被3整除；

(3)、定义：一个自然数按从右往左的第1、3、5、7、…数位，我们称为奇位，按从右往左的第2、4、6、8、…数位，我们称为偶位．例如：一个四位数，其个位与百位即奇位，十位与千位为偶位．奇位和就是把所有位于奇位上的数字相加，偶位和就是把所有位于偶位上的数字相加．请证明，若

\bar{a b c d}

的偶位和与奇位和的差是11的倍数，则

\bar{a b c d}

能被11整除．

查看试题解析

27. 如图1，两个等腰直角三角形△ABC、△EDC的顶点C重合，其中∠ABC=∠EDC=90°，连接AE，取AE中点F，连接BF，DF．小红想分析当△EDC绕着点C旋转时，图形的基本元素之间有什么不变的关系．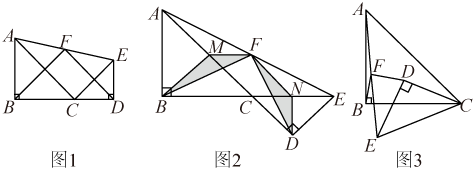

(1)、如图1，当B、C、D三个点共线时，请猜测线段BF、FD的数量关系，并直接写出；

(2)、将△EDC绕着点C顺时针旋转一定角度至图2位置，小红根据“AE中点F”这个条件，想到取AC与EC的中点M、N，分别与点F相连，再连接BM，DN，最终利用△BMF≌△FND（SAS）证明了（1）中的结论仍然成立．请你思考当△EDC绕着点C继续顺时针旋转至图3位置时，（1）中的结论是否仍然成立？若成立，请证明你的结论；若不成立，请说明理由；

(3)、连接BD，在△EDC绕点C旋转一周的过程中，△BFD的面积也随之变化．若AB=3，DE=2，请直接写出△BFD面积的最大值．

查看试题解析