山东省济南市历城区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图标是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式从左到右的变形是因式分解的是（）

A、a²－ab＝a（a－b） B、（a－3）（a＋1）＝a²－2a－3 C、ab＋bc＋d＝b（a＋c）＋d D、6a²b＝3ab·2a

查看试题解析
3. 如图，平行四边形ABCD中，AD＝5，AB＝3，AE平分∠BAD交BC边于点E，则EC等于（）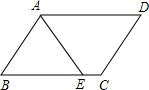

A、1 B、2 C、3 D、4

查看试题解析
4. 若关于x的方程 $x^{2} + 2 x + a = 0$ 有两个不相等的实数根，则a的值可以是（）

A、3 B、2 C、1 D、0

查看试题解析
5. 实数 $a ， b$ 在数轴上的对应点的位置如图所示，下列关系式不成立的是（）

A、 $a - 5 > b - 5$ B、 $6 a > 6 b$ C、 $- a > - b$ D、 $a - b > 0$

查看试题解析
6. 如图，在6×6方格中有两个涂有阴影的图形M、N，①中的图形M平移后位置如②所示，以下对图形M的平移方法叙述正确的是（）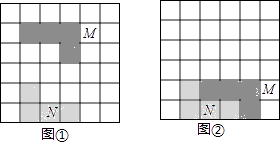

A、向右平移2个单位，向下平移3个单位 B、向右平移1个单位，向下平移3个单位 C、向右平移1个单位，向下平移4个单位 D、向右平移2个单位，向下平移4个单位

查看试题解析
7. 下列说法正确的是（）

A、三条边相等的四边形是菱形 B、对角线相等的平行四边形是矩形 C、连接矩形各边中点所得四边形是正方形 D、一组对边平行，另一组对边相等的四边形是平行四边形

查看试题解析
8. 某口罩厂平均每天可生产20万只口罩，厂家引进新技术，经过连续两次增速后，平均每天可生产30万只.若两次的增长率都为x，则可得方程（）

A、 $(20 + x)^{2} = 30$ B、 $20 (1 + x)^{2} = 30$ C、 $20 (1 + 2 x) = 30$ D、 $20 (1 + x) + 20 (1 + x)^{2} = 30$

查看试题解析
9. 已知关于的分式方程 $\frac{k}{x - 2} - \frac{3}{2 - x} = 1$ 有增根，则k＝（）．

A、－3 B、－2 C、2 D、3

查看试题解析
10. 如图，直线 $y = k x + b (k \neq 0)$ 经过点 $A (- 3 ， 2)$ ，则关于x的不等式 $k x + b < 2$ 解集为（）

A、 $x > - 3$ B、 $x < - 3$ C、 $x > 2$ D、 $x < 2$

查看试题解析
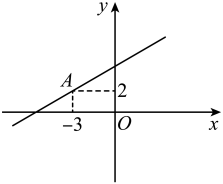11. 如图，在Rt△ABC中，∠ACB＝90°，点D是斜边AB的中点，DE平分∠ADC，BC＝4，则DE的长是（）

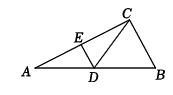A、1 B、 $\sqrt{3}$ C、2 D、4

查看试题解析
12. 如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AC＝2 $\sqrt{3}$ ， P是BC边上一动点，连接AP，把线段AP绕点A逆时针旋转60°到线段AQ，连接CQ，则线段CQ的最小值为（）

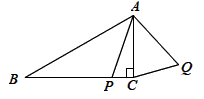A、1 B、2 C、3 D、 $\sqrt{3}$

查看试题解析

二、填空题

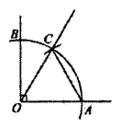
13. 因式分解：x³﹣4x²＝．

查看试题解析
14. 已知正多边形中，每一个内角都是它邻外角的4倍，则这个正多边形的边数是；

查看试题解析
15. 如图，用圆规以直角顶点O为圆心，以适当半径画一条弧交两直角边于A，B两点，若再以A点为圆心，以OA为半径画弧，与弧AB交于点C，则∠BOC等于．

查看试题解析
16. 某学习小组的成员互赠新年贺卡，共用去72张贺卡，则该学习小组有名成员；

查看试题解析
17. 如图所示的网格是由相同的小正方形组成的网格，点A，B，P是网格线的交点，则∠PAB＋∠PBA＝．

查看试题解析
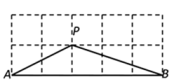18. 如图，在矩形ABCD中，AB=4，BC=8，将矩形ABCD沿EF折叠，使点C与点A重合，则折痕EF的长为．

查看试题解析

三、解答题

19.

(1)、解不等式： $\frac{2 x + 1}{3}$ －1＜ $\frac{x - 1}{2}$ ，并在数上表示其解集，

(2)、解不等式组 ${\begin{array}{l} \frac{x - 1}{2} \leq 1 \\ 4 (1 - x) < 2 x + 16 \end{array}$ ，写出该不等式组的所有非负整数解．

查看试题解析
20.

(1)、化简 $\frac{x}{x - 1} - \frac{3 x - 1}{x^{2} - 1}$ ；

(2)、先化简，再求值： $(\frac{2}{a - 1} - \frac{1}{a}) \div \frac{a^{2} + a}{a^{2} - 2 a + 1}$ ，再从－1，0，1，2四个数中选一个合适的数作为a的值代入求值．

查看试题解析
21. 解方程

(1)、 $\frac{x}{x - 2} - 1 = \frac{3}{x^{2} - 4}$ ；

(2)、x²＋2x－2＝0

查看试题解析
22. 已知：如图，AC是平行四边行ABCD的对角线，过点D作DE⊥DC，交AC于点E，过点B作BF⊥AB，交AC于点F．求证：DE＝BF．

查看试题解析
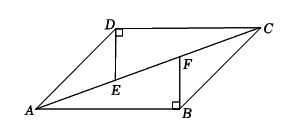23. 如图，正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求解答下列问题：

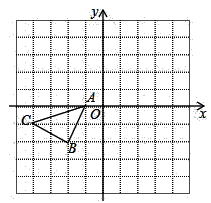(1)、△A₁B₁C₁与△ABC关于坐标原点O成中心对称，则 $B_{1}$ 的坐标为；

(2)、△A₁B₁C₁的面积为；

(3)、将△ABC绕某点逆时针旋转90°后，其对应点分别为A₂（－1，－2），B₂（1，－3），C₂（0．－5），则旋转中心的坐标为；

查看试题解析
24. 某图书馆计划选购甲、乙两种图书．已知甲图书每本价格是乙图书每本价格的2.5倍，用800元单独购买甲图书比用800元单独购买乙图书要少24本．

(1)、甲、乙两种图书每本价格分别为多少元？

(2)、如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本，且用于购买甲、乙两种图书的总经费不超过1060元，那么该图书馆最多可以购买多少本乙图书？

查看试题解析
25. 如图，在△ABC中，∠A＝60°，AB＝4cm，AC＝12cm，动点P从点A开始沿AB边以1cm/s的速度运动，动点Q从点C开始沿CA边以3cm/s的速度运动．点P和点Q同时出发，当点P到达点B时，点Q也随之停止运动，设动点的运动时间为ts（0＜t＜4），解答下列问题：

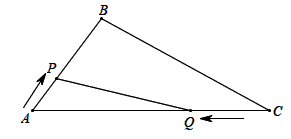(1)、当t为何值时，点A在PQ的垂直平分线上？

(2)、在运动过程中，是否存在某一时刻，使△APQ是直角三角形？若存在，求出t的值；若不存在，请说明理由．

查看试题解析
26. 阅读下列材料：
数学课上老师出示了这样一个问题：如图1，等腰Rt△PBF的直角顶点P在正方形ABCD的边AD上，斜边BF交CD于点Q，连接PQ．请探索PQ、AP、CQ的数量关系．
某学习小组的同学经过探索，交流了自己的想法：利用现在所学的旋转知识，可将△ABP旋转到△CBE位置，然后通过证明△BPQ≌△BEQ来探索数量关系．

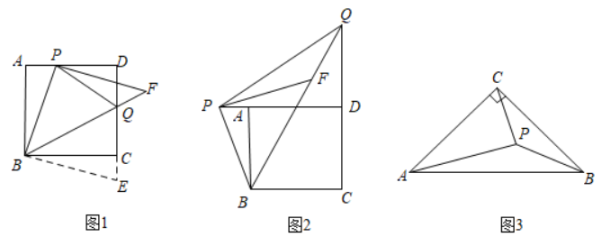(1)、（问题解决）请你根据他们的想法写出PQ、AP、CQ的数量关系是；

(2)、（学以致用）如图2，若等腰Rt△PBF的直角顶点P在正方形ABCD的边DA的延长线上，斜边BF的延长线交CD的延长线于点Q，连接PQ，猜想线段PQ，AP，CQ满足怎样的数量关系？并证明你的结论；

(3)、（思维拓展）等腰直角△ABC中，∠ACB＝90°，P为△ABC内部一点，若BC＝2．则AP＋BP＋CP的最小值＝．

查看试题解析