山东省济南市莱芜区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 用配方法解一元二次方程 , 配方正确的是( )A、 B、 C、 D、3. 顺次连接矩形各边中点得到的四边形是( )A、平行四边形 B、矩形 C、菱形 D、正方形4. 若两个相似三角形的周长之比为1∶4,则它们的面积之比为( )A、1∶2 B、1∶4 C、1∶8 D、1∶165. 以为根的一元二次方程可能是( )A、 B、 C、 D、6. 下列命题中,真命题是( )A、两组邻边分别相等的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直平分且相等的四边形是正方形7. 已知三角形的两边长为3和6,第三边的长是方程的一个根,则这个三角形的周长是( )A、12 B、13 C、12或13 D、158. 如图,在中,E是线段AC上一点, , 过点C作 , 交BE的延长线于点D.若的面积等于16,则的面积等于( )
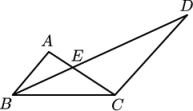 A、8 B、10 C、12 D、169. 直角三角形两条直角边长分别为和 , 则该直角三角形斜边上的中线长为( )A、 B、 C、1 D、210. 如图,在中,AD是BC边上的高,在的内部,作一个正方形PQRS,若 , , 则正方形PQRS的边长为( )
A、8 B、10 C、12 D、169. 直角三角形两条直角边长分别为和 , 则该直角三角形斜边上的中线长为( )A、 B、 C、1 D、210. 如图,在中,AD是BC边上的高,在的内部,作一个正方形PQRS,若 , , 则正方形PQRS的边长为( ) A、 B、 C、1 D、11. 如图,在平面直角坐标系中,矩形OEFG与矩形ABCD是位似图形,其中对应点C和F的坐标分别为 , , 则位似中心的坐标是( )
A、 B、 C、1 D、11. 如图,在平面直角坐标系中,矩形OEFG与矩形ABCD是位似图形,其中对应点C和F的坐标分别为 , , 则位似中心的坐标是( ) A、 B、 C、 D、12. 如图,菱形ABCD的边长为6, , 点E是AB的中点,点P是对角线AC上一动点,则的最小值是( )
A、 B、 C、 D、12. 如图,菱形ABCD的边长为6, , 点E是AB的中点,点P是对角线AC上一动点,则的最小值是( )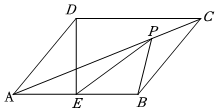 A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题
-
13. 若式子在实数范围内有意义,则x的取值范围是 .14. 若关于 的方程 有两个不相等的实数根,则 的取值范围是 .15. 计算: .16. 近期随着国家抑制房价新政策的出台,某楼盘房价连续两次下跌,由原来的每平方米10000元降至每平方米8100元,设每次降价的百分率相同,则降价百分率为.17. 如图,已知 , 点D是AC的中点, , 则AB的长为 .
 18. 将矩形纸片ABCD折叠,使点B和点D重合,折痕EF与BD交于点O.若 , , 则 .
18. 将矩形纸片ABCD折叠,使点B和点D重合,折痕EF与BD交于点O.若 , , 则 .
三、解答题
-
19. 计算:﹣(+)().20. 计算: .21. 如图,等边的边长为6,点P,D分别是BC、AC边上的点,且 , , 求CD的长.
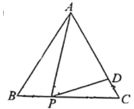 22. 已知:关于x的方程有一个根是-4,求另一个根及m的值.23. 如图,在四边形ABCD中, , , 对角线AC,BD交于点O,AC平分∠BAD.
22. 已知:关于x的方程有一个根是-4,求另一个根及m的值.23. 如图,在四边形ABCD中, , , 对角线AC,BD交于点O,AC平分∠BAD.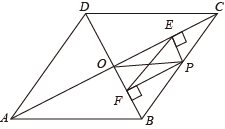 (1)、求证:四边形ABCD是菱形;(2)、点P是边BC上的动点(不包括端点),过点P作 , , 垂足分别为E,F,求证: .24. 已知一个矩形相邻的两边长分别是a,b,且 , .(1)、求此矩形的周长;(2)、若一个正方形的周长与上述矩形的周长相等,求此正方形的面积.25. 某农户生产经营一种农产品,已知这种农产品的成本价为每千克20元,经市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间满足一次函数关系,其图象如图所示.
(1)、求证:四边形ABCD是菱形;(2)、点P是边BC上的动点(不包括端点),过点P作 , , 垂足分别为E,F,求证: .24. 已知一个矩形相邻的两边长分别是a,b,且 , .(1)、求此矩形的周长;(2)、若一个正方形的周长与上述矩形的周长相等,求此正方形的面积.25. 某农户生产经营一种农产品,已知这种农产品的成本价为每千克20元,经市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间满足一次函数关系,其图象如图所示. (1)、求y与x之间的函数关系式;(2)、该农户想要每天获得150元的利润,又要让利消费者,销售价应定为每千克多少元?26. 如图,在边长为4的正方形ABCD中,E,F分别是BC,CD的中点,连接AE,BF交于点G.
(1)、求y与x之间的函数关系式;(2)、该农户想要每天获得150元的利润,又要让利消费者,销售价应定为每千克多少元?26. 如图,在边长为4的正方形ABCD中,E,F分别是BC,CD的中点,连接AE,BF交于点G.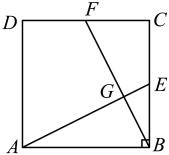 (1)、AE,BF之间有怎样的数量关系和位置关系?请说明理由;(2)、求四边形FGEC的面积.27. 某校数学活动小组探究了如下数学问题:
(1)、AE,BF之间有怎样的数量关系和位置关系?请说明理由;(2)、求四边形FGEC的面积.27. 某校数学活动小组探究了如下数学问题: (1)、问题发现:如图1,中, , . 点P是底边BC上一点,连接AP,以AP为腰作等腰 , 且 , 连接CQ、则BP和CQ的数量关系是;(2)、变式探究:如图2,中, , . 点P是腰AB上一点,连接CP,以CP为底边作等腰 , 连接AQ,判断BP和AQ的数量关系,并说明理由;(3)、问题解决:如图3,在正方形ABCD中,点P是边BC上一点,以DP为边作正方形DPEF,点Q是正方形DPEF两条对角线的交点,连接CQ.若正方形DPEF的边长为 , , 求正方形ABCD的边长.
(1)、问题发现:如图1,中, , . 点P是底边BC上一点,连接AP,以AP为腰作等腰 , 且 , 连接CQ、则BP和CQ的数量关系是;(2)、变式探究:如图2,中, , . 点P是腰AB上一点,连接CP,以CP为底边作等腰 , 连接AQ,判断BP和AQ的数量关系,并说明理由;(3)、问题解决:如图3,在正方形ABCD中,点P是边BC上一点,以DP为边作正方形DPEF,点Q是正方形DPEF两条对角线的交点,连接CQ.若正方形DPEF的边长为 , , 求正方形ABCD的边长.