山东省济南市槐荫区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 第24届冬季奥林匹克运动会于2022年2月4日至2月20日在中国北京市和张家口市联合举办，以下是参选的冬奥会会徽设计的部分图形，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列几何体中，主视图是圆形的是（）

A、 B、 C、 D、

查看试题解析
3. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）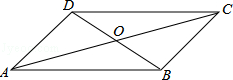

A、AB//DC，AD//BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB//DC，AD=BC

查看试题解析
4. 如图， $△ A B C$ 沿直线m向右平移 $2 cm$ ，得到 $△ D E F$ ，下列说法错误的是（）

A、 $A C // D F$ B、 $A B = D E$ C、 $C F = 2 cm$ D、 $D E = 2 cm$

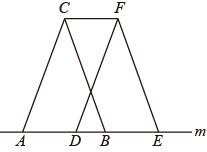查看试题解析
5. 下列各式能用完全平方公式进行分解因式的是（）

A、 $x^{2} + 1$ B、 $x^{2} - 2 x - 1$ C、 $x^{2} + 3 x + 9$ D、 $x^{2} - x + \frac{1}{4}$

查看试题解析
6. 化简 $\frac{a^{2} + a}{a^{2} - 1}$ 的结果是（）

A、 $\frac{a + 1}{a - 1}$ B、 $\frac{a}{a + 1}$ C、 $\frac{a}{a - 1}$ D、 $a + 1$

查看试题解析
7. 若关于x的一元二次方程 $a x^{2} - 2 x + 1 = 0$ 有实数根，则a应满足（）

A、 $a \leq 1$ B、 $a \geq 1$ C、 $a \geq - 1$ 且 $a \neq 0$ D、 $a \leq 1$ 且 $a \neq 0$

查看试题解析
8. 小李和小王两位同学想从篮球、足球、游泳三项体育项目中任选一项进行体育锻炼，则小李和小王两位同学选择同一种体育项目的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{5}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析
9. 九年级（3）班小王和小张两人练习跳绳，小王每分钟比小张少跳60个，小王跳120个所用的时间和小张跳180个所用的时间相等．设小王跳绳速度为x个每分钟，则列方程正确的是（）

A、 $\frac{120}{x + 60} = \frac{180}{x}$ B、 $\frac{120}{x} = \frac{180}{x - 60}$ C、 $\frac{120}{x} = \frac{180}{x + 60}$ D、 $\frac{120}{x - 60} = \frac{180}{x}$

查看试题解析
10. 如图，将 $△ A B C$ 绕点A按逆时针方向旋转110°得到 $△ A B^{'} C^{'}$ ，连接 $B B^{'}$ ，若 $A C^{'} ∥ B B^{'}$ ，则 $∠ C A B^{'}$ 的度数为（）

A、75° B、80° C、85° D、90°

查看试题解析
11. 如图，在Rt△ABC中，∠C=90°，D，E分别为CA，CB的中点，BF平分∠ABC，交DE于点F，若AC=2 $\sqrt{5}$ ， BC=4，则DF的长为（）

A、0.5 B、1 C、1.5 D、2

查看试题解析
12. 如图，菱形ABCD中， $∠ B A D = 60 °$ ， AC与BD交于点O，E为CD延长线上一点，且 $C D = D E$ ，连接BE，分别交AC，AD于点F、G，连接OG，则下列结论：
① $O G = \frac{1}{2} A B$ ；② $S_{四边形 O D G F} > S_{△ A B F}$ ；③由点A、B、D、E构成的四边形是菱形；④ $S_{△ A C D} = 4 S_{△ B O G}$ ，其中正确的结论是（）

A、①② B、①②③ C、①③④ D、②③④

查看试题解析

二、填空题

13. 因式分解： $m^{2} - 4 m =$ .

查看试题解析
14. 一个正多边形的一个外角等于45°，则这个正多边形的边数是．

查看试题解析
15. 关于x的一元二次方程 $x^{2} + m x - 5 = 0$ 有一根是 $x = - 1$ ，则另外一根是.

查看试题解析
16. 如图，EF过平行四边形ABCD对角线的交点O，交AD于点E，交BC于点F，若平行四边形ABCD的周长是30，OE=3，则四边形ABFE的周长是．

查看试题解析
17. 在平面直角坐标系中，▱OABC的边OC落在x轴的正半轴上，且点C（4，0），B（6，2），直线y=2x+1以每秒1个单位的速度向右平移，经过秒该直线可将▱OABC的面积平分.

查看试题解析
18. 如图，正方形 $A B C D$ 的边长为4， $E$ 为 $B C$ 上一点，且 $B E = 1$ ， $F$ 为 $A B$ 边上的一个动点，连接 $E F$ ，以 $E F$ 为边向右侧作等边 $Δ E F G$ ，连接 $C G$ ，则 $C G$ 的最小值为.

查看试题解析

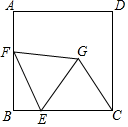
三、解答题

19. 解方程： $x^{2} - 4 x - 2 = 0$

查看试题解析
20. 计算： $\frac{2 x}{x^{2} - 4} - \frac{1}{x + 2}$

查看试题解析
21. 如图，在 $▱ A B C D$ 中，对角线AC和BD相交于点O， $B D ⊥ A D$ ， $A B = 10$ ， $B C = 8$ ．求OB的长．

查看试题解析
22. 如图，方格纸中的每个小正方形的边长都为1，在建立平面直角坐标系后，△ABC的顶点均在格点上．
（ 1 ）以点A为旋转中心，将△ABC绕点A顺时针旋转90°得到△AB₁C₁ ，画出△AB₁C₁；
（ 2 ）画出△ABC关于原点O成中心对称的△A₂B₂C₂ ，若点B的坐标为（-2，-2），则点B₂的坐标为 ▲ ．
（ 3 ）若△A₂B₂C₂可看作是由△AB₁C₁绕点P顺时针旋转90°得到的，则点P的坐标为 ▲ .

查看试题解析
23. 小明从商店里购买3张正面分别印有2022年北京冬奥会吉祥物卡片（卡片的形状、大小、质地都相同），其中印有“冰墩墩”图片的卡片2张、印有“雪容融”图片的卡片1张，将这三张正面卡片背面朝上、洗匀．

(1)、若从中任意抽取1张，抽得卡片上的图案恰好为“冰墩墩”的概率是；

(2)、若先从中任意抽取1张，记录后放回、洗匀，再从中任意抽取1张，请用树状图或列表的方法求两次抽取的卡片刚好是1张是“冰墩墩”另1张是“雪容融”的概率．

查看试题解析
24. 如图，一长方形草坪长50米，宽30米，在草坪上有两条互相垂直且宽度相等的长方形小路（阴影部分），非阴影部分的面积是924米 $^{2}$ ．

(1)、求小路的宽度；

(2)、每平方米小路的建设费用为200元，求修建两条小路的总费用．

查看试题解析
25. 在▱ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF=AE，连接BF，AF．

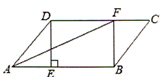(1)、求证：四边形BFDE是矩形；

(2)、若AF平分∠BAD，且AE=3，DE=4，求矩形BFDE的面积．

查看试题解析
26. 如图，平面直角坐标系中，O是坐标原点，直线 $y = k x + 15 (k \neq 0)$ 经过点 $C (3 ， 6)$ ，与x轴交于点A，与y轴交于点B．线段CD平行于x轴，交直线 $y = \frac{3}{4} x$ 于点D，连接OC、AD．

(1)、填空：k= ，点A的坐标是；

(2)、求证：四边形OADC是平行四边形；

(3)、动点P从点O出发，沿对角线OD以每秒1个单位长度的速度向点D运动，直到点D为止；动点Q同时从点D出发，沿对角线DO以每秒1个单位长度的速度向点O运动，直到点O为止．设两个点的运动时间均为t秒．
①当 $t = 1$ 时， $△ C P Q$ 的面积是；
②是否存在t的值使得四边形CPAQ为矩形，若存在，请求出t的值；若不存在，请说明理由．

查看试题解析
27. 如图1，四边形ABCD和四边形DEFG都是正方形，点A在DG上，连接AE，CG．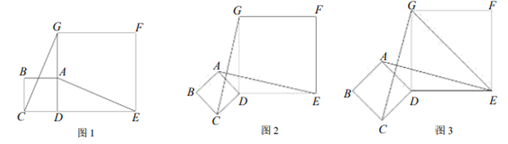

(1)、求证： $A E = C G$ ；

(2)、猜想：AE与CG之间的位置关系，并证明你的猜想；

(3)、在其它条件不变的前提下，如果将正方形ABCD绕着点D按逆时针旋转任意角度（如图2）．那么（2）中结论是否还成立？若成立，请给出证明；若不成立，请说明理由；

(4)、如图3，将正方形ABCD绕着点D旋转到某一位置时恰好使得 $A D ∥ E G$ ， $A E = G E$ ．当正方形DEFG的边长为 $\sqrt{2}$ 时，请直接写出正方形ABCD的边长．

查看试题解析