山东省济南市钢城区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 已知2x=3y(y≠0),则下面结论成立的是( )A、 = B、 = C、 = D、 =2. 下列式子是最简二次根式的是( )A、 B、 C、 D、3. 已知四边形ABCD是平行四边形,当AC=BD时,它是( )A、正方形 B、菱形 C、矩形 D、平行四边形4. 下列计算中,正确的是( )A、 B、 C、 D、5. 若关于x的一元二次方程有两个实数根,则实数k的取值范围是( )A、且 B、 C、 D、且6. 在菱形中,对角线与相交于点O,E是的中点, , , 则的长为( )
 A、 B、 C、 D、7. 实数a,b在数轴上对应点的位置如图所示,化简的结果是:( )
A、 B、 C、 D、7. 实数a,b在数轴上对应点的位置如图所示,化简的结果是:( ) A、 B、 C、 D、b8. 根据方程x2﹣3x﹣5=0可列表如下( )
A、 B、 C、 D、b8. 根据方程x2﹣3x﹣5=0可列表如下( )x
﹣3
﹣2
﹣1
…
4
5
6
x2﹣3x﹣5
13
5
﹣1
…
﹣1
5
13
则x的取值范围是( )
A、﹣3<x<﹣2或4<x<5 B、﹣2<x<﹣1或5<x<6 C、﹣3<x<﹣2或5<x<6 D、﹣2<x<﹣1或4<x<59. 在中,点D是边上的点(与B,C两点不重合),过点D作 , 分别交 , 于E,F两点,下列说法正确的是( )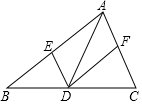 A、若 , 则四边形是矩形 B、若垂直平分 , 则四边形是矩形 C、若 , 则四边形是菱形 D、若平分 , 则四边形是菱形10. 今年为庆祝共青团成立100周年,教体局举行篮球友谊赛,初赛采用单循环制(每两支球队之间都进行一场比赛),据统计,比赛共进行了28场,则一共邀请了多少支球队参加比赛?设一共邀请了x支球队参加比赛.根据题意可列方程是( )A、 B、 C、 D、11. 如图,中,A,B两个顶点在x轴的上方,点C的坐标是 . 以点C为位似中心,在x轴的下方作的位似图形 , 并把的边长放大到原来的2倍.设点B的对应点的横坐标是m,则点B的横坐标是( )
A、若 , 则四边形是矩形 B、若垂直平分 , 则四边形是矩形 C、若 , 则四边形是菱形 D、若平分 , 则四边形是菱形10. 今年为庆祝共青团成立100周年,教体局举行篮球友谊赛,初赛采用单循环制(每两支球队之间都进行一场比赛),据统计,比赛共进行了28场,则一共邀请了多少支球队参加比赛?设一共邀请了x支球队参加比赛.根据题意可列方程是( )A、 B、 C、 D、11. 如图,中,A,B两个顶点在x轴的上方,点C的坐标是 . 以点C为位似中心,在x轴的下方作的位似图形 , 并把的边长放大到原来的2倍.设点B的对应点的横坐标是m,则点B的横坐标是( ) A、 B、 C、 D、12. 在矩形中, , , 将矩形沿折叠,点B落在点E处,线段交于定O,过O作于点G,于点H,则的值为( )
A、 B、 C、 D、12. 在矩形中, , , 将矩形沿折叠,点B落在点E处,线段交于定O,过O作于点G,于点H,则的值为( ) A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
13. 若二次根式 在实数范围内有意义,则x的取值范围是 .14. 如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为米.
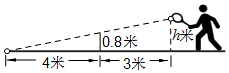 15. 若m,n为一元二次方程的两个实数根,则的值为 .16. 如图,在正方形内作等边 , 连接 , , 则的度数为 .
15. 若m,n为一元二次方程的两个实数根,则的值为 .16. 如图,在正方形内作等边 , 连接 , , 则的度数为 . 17. 如图,点P为的边上的一点,添加 , 可以使与相似.
17. 如图,点P为的边上的一点,添加 , 可以使与相似. 18. 如图,在矩形中, , , 点P是不与A,D重合的两点,过点P分别作和的垂线,垂足分别为E,F,则的值是 .
18. 如图,在矩形中, , , 点P是不与A,D重合的两点,过点P分别作和的垂线,垂足分别为E,F,则的值是 . 19. 如图,在矩形中,对角线与相交于点O, , , 求矩形的面积 .
19. 如图,在矩形中,对角线与相交于点O, , , 求矩形的面积 .
三、解答题
-
20. 解方程: .21. 计算:22. 疫情期间居民为了减少外出,更愿意选择线上购物,某购物平台今年二月份注册用户50万人,四月份达到了72万人,假设二月份至四月份的月平均增长率为 .(1)、求的值.(2)、若保持这个增长率不变,五月份注册用户能否达到85万人?为什么?23. 如图,在 和 中, , .
 (1)、求证: ;(2)、若 , ,求 的长.24. 2022年冬奥会吉祥物冰墩墩深受人们喜爱,冬奥会特许商店将进货价为每个30元的冰墩墩饰品以40元的价格售出,平均每月能售出600个,调查表明:这种冰墩墩饰品的售价每上涨1元,其销售量就减少10个,同时规定售价在40-60元范围内.(1)、当售价上涨x元时,销售量为个;(2)、为了实现销售这种饰品平均每月10000元的销售利润,每个饰品应定为多少元?这时售出冰墩墩饰品多少个?25. 阅读下列解题过程:
(1)、求证: ;(2)、若 , ,求 的长.24. 2022年冬奥会吉祥物冰墩墩深受人们喜爱,冬奥会特许商店将进货价为每个30元的冰墩墩饰品以40元的价格售出,平均每月能售出600个,调查表明:这种冰墩墩饰品的售价每上涨1元,其销售量就减少10个,同时规定售价在40-60元范围内.(1)、当售价上涨x元时,销售量为个;(2)、为了实现销售这种饰品平均每月10000元的销售利润,每个饰品应定为多少元?这时售出冰墩墩饰品多少个?25. 阅读下列解题过程:请回答下列问题:
(1)、归纳:观察上面的解题过程,请直接写出下列各式的结果.① ;② .(2)、应用:求 的值;(3)、拓展: . (直接写出答案)

