山东省东营市广饶县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 下列计算结果,正确的是( )A、 =-3 B、 + = C、 - =1 D、 =52. 下列一元二次方程中,有两个不相等的实数根的方程是( )A、 B、 C、 D、3. 已知 ,下列变形错误的是( )A、 B、 C、 D、4. 已知四边形ABCD是平行四边形,下列说法:①当 时,它是矩形;② 时,它是菱形;③当 时,它是菱形;④当 时,它是正方形.其中正确的有( )A、①② B、②④ C、③④ D、②5. 一元二次方程x(x﹣2)=2﹣x的根是( )A、x=﹣1 B、x=2 C、x1=1,x2=2 D、x1=﹣1,x2=26. 如图所示,给出下列条件:① ;② ;③ ;④ ,其中单独能够判定 的个数为( )
 A、 B、 C、 D、7. 如图,O是矩形ABCD的对角线交点,AE平分∠BAD,∠AOD=120°,∠AEO的度数为( )
A、 B、 C、 D、7. 如图,O是矩形ABCD的对角线交点,AE平分∠BAD,∠AOD=120°,∠AEO的度数为( ) A、15° B、25° C、30° D、35°8. 一次会议上,每两个参加会议的人都互相握了一次手,有人统计一共共握66次手.若设这次会议到会的人数为x人,依题意可列方程( )A、x(x﹣1)=66 B、=66 C、x(1+x)=66 D、x(x﹣1)=669. 如图,在平行四边形中,E为边上的点,若 , 交于F,则等于( )
A、15° B、25° C、30° D、35°8. 一次会议上,每两个参加会议的人都互相握了一次手,有人统计一共共握66次手.若设这次会议到会的人数为x人,依题意可列方程( )A、x(x﹣1)=66 B、=66 C、x(1+x)=66 D、x(x﹣1)=669. 如图,在平行四边形中,E为边上的点,若 , 交于F,则等于( )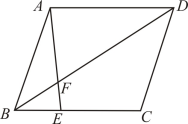 A、 B、 C、 D、10. 如图,在正方形中,点O是对角线的交点,过点O作射线分别交于点 , 且 , 交于点 . 给出下列结论:;;四边形的面积为正方形面积的; . 其中正确的是( )
A、 B、 C、 D、10. 如图,在正方形中,点O是对角线的交点,过点O作射线分别交于点 , 且 , 交于点 . 给出下列结论:;;四边形的面积为正方形面积的; . 其中正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
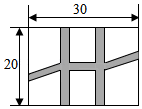
11. 已知 , 则= .12. 如果代数式有意义,那么x的取值范围是 .13. 如果关于x的一元二次方程(m+3)x2+3x+m2﹣9=0有一个解是0,那么m的值是 .14. 一个菱形的周长为52cm,一条对角线长为10cm,则其面积为cm2.15. 如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为468m2 , 那么小道进出口的宽度应为 m.
 16. 如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半,已知BC=2,△ABC平移的距离为 .
16. 如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半,已知BC=2,△ABC平移的距离为 . 17. 如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与点B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF的最小值等于 .
17. 如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与点B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF的最小值等于 . 18. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4.点 , , 分别在AC、BC、AB上,且四边形C是正方形,点 , , 分别在、 , 上,且四边形是正方形,则线段的长度是 .
18. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4.点 , , 分别在AC、BC、AB上,且四边形C是正方形,点 , , 分别在、 , 上,且四边形是正方形,则线段的长度是 .
三、解答题
-
19. 按要求化简或解方程.(1)、;(2)、;(3)、(x+1)(3x﹣1)=1(解方程).20. 已知关于x的一元二次方程x2﹣(m+3)x+3m=0.(1)、求证:无论m取任何实数,方程总有实数根;(2)、若等腰三角形的其中一边为4,另两边是这个方程的两根,求m的值.21. 如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
 (1)、画出位似中心点O;(2)、直接写出△ABC与△A′B′C′的位似比;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出△A′B′C′各顶点的坐标.22. 如图,在矩形中,、相交于点O,过点D作 , 且使得 , 连接 , .
(1)、画出位似中心点O;(2)、直接写出△ABC与△A′B′C′的位似比;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出△A′B′C′各顶点的坐标.22. 如图,在矩形中,、相交于点O,过点D作 , 且使得 , 连接 , . (1)、求证:;(2)、判断四边形的形状,并说明理由.23. 2022年北京冬奥会吉祥物深受大家的喜欢,某特许零售店的冬奥会吉祥物销售量日益火爆.据统计,该店2022年1月的“冰墩墩”销量为1万件,2022年3月的“冰墩墩”销量为1.21万件.(1)、求该店“冰墩墩”销量的月平均增长率;(2)、该零售店4月将采用提高售价的方法增加利润,根据市场调研得出结论:如果将进
(1)、求证:;(2)、判断四边形的形状,并说明理由.23. 2022年北京冬奥会吉祥物深受大家的喜欢,某特许零售店的冬奥会吉祥物销售量日益火爆.据统计,该店2022年1月的“冰墩墩”销量为1万件,2022年3月的“冰墩墩”销量为1.21万件.(1)、求该店“冰墩墩”销量的月平均增长率;(2)、该零售店4月将采用提高售价的方法增加利润,根据市场调研得出结论:如果将进价80元的“冰墩墩”按每件100元出售,每天可销售500件,在此基础上售价每涨1元,那么每天的销售量就会减少10件,该零售店要想每天获得12000元的利润,且销量尽可能大,则每件商品的售价应该定为多少元?
24. 学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1).如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH,两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度. 25. 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点A出发沿AC方向以4cm/s的速度向点C匀速运动,同时点E从点B出发沿BA方向以2cm/s的速度向点A匀速运动,设点D、E运动的时间是t秒(0<t<1S),过点D作DF⊥BC于点F,连接DE,EF.
25. 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点A出发沿AC方向以4cm/s的速度向点C匀速运动,同时点E从点B出发沿BA方向以2cm/s的速度向点A匀速运动,设点D、E运动的时间是t秒(0<t<1S),过点D作DF⊥BC于点F,连接DE,EF. (1)、求证:四边形AEFD是平行四边形;(2)、当t为何值时,四边形AEFD为菱形?说明理由;(3)、当t为何值时,△ADE与△ABC相似?说明理由.26. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)、求证:四边形AEFD是平行四边形;(2)、当t为何值时,四边形AEFD为菱形?说明理由;(3)、当t为何值时,△ADE与△ABC相似?说明理由.26. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试. (1)、如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为6cm.那么灯泡离地面的高度为多少.(2)、不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子 , 的长度和为多少?(3)、有n个边长为a的正方形按图3摆放,测得横向影子 , 的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
(1)、如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为6cm.那么灯泡离地面的高度为多少.(2)、不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子 , 的长度和为多少?(3)、有n个边长为a的正方形按图3摆放,测得横向影子 , 的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)