山东省东营市东营区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 下列各式中属于最简二次根式的是( )A、 B、 C、 D、2. 已知反比例函数 ,则下列描述错误的是( )A、图象位于第一,第三象限 B、图象必经过点 C、图象不可能与坐标轴相交 D、 随 的增大而减小3. 一元二次方程的根的情况为( )A、无实数根 B、有两个不等的实数根 C、有两个相等的实数根 D、不能判定4. 如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC, ,DE=6cm,则BC的长为( )
 A、9cm B、12cm C、15cm D、18cm5. 电影《长津湖》上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达18亿元,将增长率记作x,则方程可以列为( )A、2+2x+2x2=18 B、2(1+x)2=18 C、(1+x)2=18 D、2+2(1+x)+2(1+x)2=186. 如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
A、9cm B、12cm C、15cm D、18cm5. 电影《长津湖》上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达18亿元,将增长率记作x,则方程可以列为( )A、2+2x+2x2=18 B、2(1+x)2=18 C、(1+x)2=18 D、2+2(1+x)+2(1+x)2=186. 如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( ) A、(0,0),2 B、(2,2), C、(2,2),2 D、(1,1),7. 若 , 则等于( )A、5 B、-1 C、13 D、18. 在同一平面直角坐标系中,函数与 (k为常数且)的图象大致是( )A、
A、(0,0),2 B、(2,2), C、(2,2),2 D、(1,1),7. 若 , 则等于( )A、5 B、-1 C、13 D、18. 在同一平面直角坐标系中,函数与 (k为常数且)的图象大致是( )A、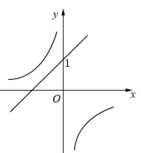 B、
B、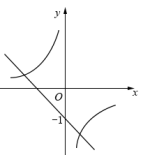 C、
C、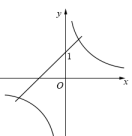 D、
D、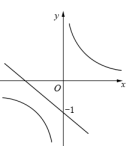 9. 如图,点A在x轴正半轴上,点B在第二象限内,直线AB交y轴于点F,轴,垂足是C,反比例函数的图象分别交BC,AB于点 , E,若 , 则△ABC的面积为( )
9. 如图,点A在x轴正半轴上,点B在第二象限内,直线AB交y轴于点F,轴,垂足是C,反比例函数的图象分别交BC,AB于点 , E,若 , 则△ABC的面积为( ) A、 B、8 C、9 D、1010. 已知菱形 , E、F是动点,边长为5, , , 则下列命题中正确的是( )
A、 B、8 C、9 D、1010. 已知菱形 , E、F是动点,边长为5, , , 则下列命题中正确的是( )①;②为等边三角形;③的边长最小值为;④若 , 则 .
 A、①② B、①③ C、①②④ D、①②③
A、①② B、①③ C、①②④ D、①②③二、填空题
-
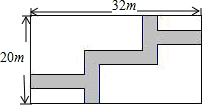
11. 若二次根式 在实数范围内有意义,则x的取值范围为 .12. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系为(用“<”连接).13. 如果关于x的一元二次方程的一个解是 , 则2023-a-b= .14. 计算: = .15. 如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2 , 求道路的宽若设道路宽为xm,则根据题意可列方程为
 16. 如图,点A在曲线到上,点B在双曲线上,ABx轴,点C是x轴上一点,连接、 , 若的面积是6,则k的值为 .
16. 如图,点A在曲线到上,点B在双曲线上,ABx轴,点C是x轴上一点,连接、 , 若的面积是6,则k的值为 . 17. 如图,已知点A、B分别在反比例函数 , 的图象上,且 ,则 的值为 .
17. 如图,已知点A、B分别在反比例函数 , 的图象上,且 ,则 的值为 . 18. 如图,在矩形中, , , 连接 , 以对角线为边,按逆时针方向作矩形 , 使矩形矩形;再连接 , 以对角线为边,按逆时针方向作矩形 , 使矩形矩形 , …,按照此规律作下去.若矩形的面积记作 , 矩形的面积记作 , 矩形的面积记作 , …,则的值为 .
18. 如图,在矩形中, , , 连接 , 以对角线为边,按逆时针方向作矩形 , 使矩形矩形;再连接 , 以对角线为边,按逆时针方向作矩形 , 使矩形矩形 , …,按照此规律作下去.若矩形的面积记作 , 矩形的面积记作 , 矩形的面积记作 , …,则的值为 .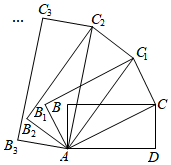
三、解答题
-
19.(1)、计算:;(2)、解方程: .20. 如图,点 的坐标为 ,点 的坐标为
①以点 为旋转中心,将 顺时针方向旋转90°,得到 ;
②以点 为位似中心,将 放大 ,使相似比为 ,且点 在第三象限.
(1)、在图中画出 和 ;(2)、请直接写出点 的坐标:( , )(3)、在上面的(2)问下,直接写出在线段 上的任意动点 的对应点 的坐标:( , ). 21. 如图:在平面直角坐标系中,菱形 的顶点D在y轴上,A,C两点的坐标分别为 ,直线 与双曲线: 交于C, 两点.
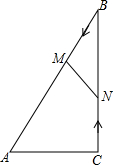
21. 如图:在平面直角坐标系中,菱形 的顶点D在y轴上,A,C两点的坐标分别为 ,直线 与双曲线: 交于C, 两点.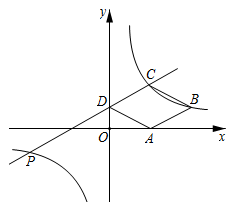 (1)、求双曲线 的函数关系式及m的值;(2)、判断点B是否在双曲线上,并说明理由;(3)、当 时,请直接写出x的取值范围.22. 如图,有一块形状为的斜板余料.已知 , , , 要把它加工成一个形状为平行四边形的工件,使在上,D,E两点分别在 , 上,且 , 求平行四边形的面积为多少?
(1)、求双曲线 的函数关系式及m的值;(2)、判断点B是否在双曲线上,并说明理由;(3)、当 时,请直接写出x的取值范围.22. 如图,有一块形状为的斜板余料.已知 , , , 要把它加工成一个形状为平行四边形的工件,使在上,D,E两点分别在 , 上,且 , 求平行四边形的面积为多少? 23. 新华商场销售某种商品,每件进货价为40元,市场调研表明:当销售价为80元时,平均每天能售出20件;在每件盈利不少于25元的前提下,经过一段时间销售,当销售价每降低1元时,平均每天就能多售出2件.(1)、若降价2元,则平均每天销售数量为件;(2)、当每件商品定价多少元时,该商场平均每天销售某种商品利润达到1200元?
23. 新华商场销售某种商品,每件进货价为40元,市场调研表明:当销售价为80元时,平均每天能售出20件;在每件盈利不少于25元的前提下,经过一段时间销售,当销售价每降低1元时,平均每天就能多售出2件.(1)、若降价2元,则平均每天销售数量为件;(2)、当每件商品定价多少元时,该商场平均每天销售某种商品利润达到1200元?