山东省滨州市滨城区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式中，是最简二次根式的是（　　）

A、 $\sqrt{24}$ B、 $\sqrt{12}$ C、 $\sqrt{30}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 下列各组数中，能构成直角三角形的为（）

A、1，1，2 B、15，21，25 C、7，24，25 D、6，12，13

查看试题解析
3. 如图，四边形ABCD为平行四边形，作 $∠ B A D$ 的平分线AE，交 $D C$ 边于点 $E$ ，若 $∠ D E A = 30 °$ ，则 $∠ C$ 的度数为（）

A、 $45 °$ B、 $60 °$ C、 $80 °$ D、 $120 °$

查看试题解析
4. 如图是自动测温仪记录的图象，它反映了某市的春季某天气温T如何随时间t的变化而变化．下列从图象中得到的信息错误的是（）

A、4点时气温达最低 B、14点到24点之间气温持续下降 C、0点到14点之间气温持续上升 D、14点时气温达最高是8℃

查看试题解析
5. 实数a、b在数轴上的位置如图，则化简 $\sqrt{(a - b)^{2}}$ 的结果是（）

A、 $a + b$ B、 $a - b$ C、 $- a + b$ D、 $- a - b$

查看试题解析
6. 如图，O为菱形ABCD的对角线的交点，DE∥AC，CE∥BD，若AC＝6，BD＝8，则线段OE的长为（　　）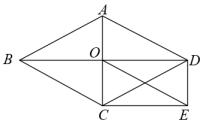

A、3 B、 $\sqrt{5}$ C、5 D、6

查看试题解析
7. 如图，点A表示的数为x，则 $x^{2} - 2 \sqrt{2}$ 的值为（）

A、 $- \sqrt{2}$ B、 $- 3 \sqrt{2}$ C、 $4 - 2 \sqrt{2}$ D、 $2 - 2 \sqrt{2}$

查看试题解析
8. 如图，已知四边形 $A B C D$ ，下列说法中正确的是（）

A、若 $A C ⊥ B D$ ， $A C = B D$ ，则四边形 $A B C D$ 是矩形 B、若 $A C ⊥ B D$ ， $A B = A D$ ， $C B = C D$ 则四边形 $A B C D$ 是菱形 C、若 $A B = B C = C D = A D$ ，则四边形 $A B C D$ 是正方形 D、若 $A D = B C$ ， $A B = C D$ ，则四边形 $A B C D$ 是平行四边形

查看试题解析
9. 一次函数 $y = - 5 x - 2$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 如图，在 $△ A B C$ 中， $C D ⊥ A B$ ，垂足为D，E为 $B C$ 边的中点， $A B = 4 ， A C = 2 ， D E = \sqrt{3}$ ，则 $∠ A C D$ （）

A、 $15 °$ B、 $30 °$ C、 $22.5 °$ D、 $45 °$

查看试题解析
11. 我们知道，若ab＞0．则有 ${\begin{array}{l} a > 0 \\ b > 0 \end{array}$ 或 ${\begin{array}{l} a < 0 \\ b < 0 \end{array}$ ．如图，直线y＝kx＋b与y＝mx＋n分别交x轴于点A（－0.5，0）、B（2，0），则不等式（kx＋b）（mx＋n）＞0的解集是（　　）

A、x＞2 B、－0.5＜x＜2 C、0＜x＜2 D、x＜－0.5或x＞2

查看试题解析
12. 如图，正方形ABCD中，AB＝12，点E在边BC上，BE＝EC，将△DCE沿DE对折至△DFE，延长EF交边AB于点G，连接DG、BF，给出以下结论：①△DAG≌△DFG；②BG＝2AG；③S_△^DGF＝120；④S_△BEF＝ $\frac{72}{5}$ ；⑤BF∥DE．其中正确结论的个数是（　　）

A、5 B、4 C、3 D、2

查看试题解析

二、解答题

13. 计算：

(1)、 $\sqrt{2} \times \sqrt{6} - (5 \sqrt{48} - 4 \sqrt{27}) \div 2 \sqrt{3}$ ；

(2)、 $(7 + 4 \sqrt{3}) (7 - 4 \sqrt{3}) - (\sqrt{3} - 1)^{2}$ ．

查看试题解析
14. 为迎接建党一百周年，学校组织了六次党史知识测试，甲、乙两名同学部分成绩如图所示，已知甲、乙两名同学六次成绩的平均数相等．

(1)、计算甲同学成绩的平均数，直接写出乙同学第六次成绩；

(2)、甲同学成绩的中位数和众数分别为和，乙同学成绩的中位数和众数分别为和；

(3)、若乙同学成绩的方差为 $s_{乙}^{2} = 33.3$ ，请计算甲同学成绩的方差，并比较哪个同学的成绩较稳定？

查看试题解析
15. 如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC、BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB延长线于点E，连接OE．

(1)、求证：四边形ABCD是菱形；

(2)、若 $A B = \sqrt{5}$ ， OE＝2，求菱形ABCD的面积．

查看试题解析
16. 已知函数y₁=2x－1的图像与x、y轴分别交与A，B两点，y₂=－0.5x＋1的图像与x、y轴分别交与C，D两点，两直线相交于点E．求下列问题：

(1)、根据题意画出图像的草图；

(2)、求点E的坐标；

(3)、求四边形AEDO的面积．

查看试题解析
17. 冰墩墩（BingDwenDwen），是2022年北京冬季奥运会的吉祥物．将熊猫形象与富有超能量的冰晶外壳相结合，头部外壳造型取自冰雪运动头盔，装饰彩色光环，整体形象酷似航天员．冬奥会来临之际，冰墩墩玩偶非常畅销．小冬在某网店选中A，B两款冰墩墩玩偶，决定从该网店进货并销售．两款玩偶的进货价和销售价如下表：

A款玩偶
B款玩偶
进货价（元/个）
20
15
销售价（元/个）
28
20

(1)、第一次小冬550元购进了A，B两款玩偶共30个，求两款玩偶各购进多少个．

(2)、第二次小冬进货时，网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半．小冬计划购进两款玩偶共30个，应如何设计进货方案才能获得最大利润，最大利润是多少？

查看试题解析
18. 如图，直线l₁：y＝kx+1与x轴交于点D，直线l₂：y＝﹣x+b与x轴交于点A，且经过定点B（﹣1，5），直线l₁与l₂交于点C（2，m）．

(1)、填空：k＝；b＝；m＝；

(2)、在x轴上是否存在一点E，使△BCE的周长最短？若存在，请求出点E的坐标；若不存在，请说明理由．

(3)、若动点P在射线DC上从点D开始以每秒1个单位的速度运动，连接AP，设点P的运动时间为t秒．是否存在t的值，使△ACP和△ADP的面积比为1：3？若存在，直接写出t的值；若不存在，请说明理由．

查看试题解析

三、填空题

19. 若式子 $\sqrt{x + 1}$ 在实数范围内有意义，则x的取值范围是 .

查看试题解析
20. 某校拟招聘一批优秀教师，其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分，综合成绩笔试、试讲、面试的占比为2：2：1，则该名教师的综合成绩为．

查看试题解析
21. 一个三角形两条边长为3和4，当第三条边长为时，此三角形为直角三角形．

查看试题解析
22. 如图，直线L经过正方形 $A B C D$ 的顶点A，分别过点B、D作 $D E ⊥ l$ 于点E， $B F ⊥ l$ 于点F，若 $D E = 4$ ， $B F = 5$ ，则 $E F$ 的长为．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ B A C = 9 0^{∘}$ ， $A B = 5$ ， $A C = 12$ ， P为边 $B C$ 上一动点， $P E ⊥ A B$ 于E， $P F ⊥ A C$ 于F，M为 $E F$ 中点，则 $A M$ 的取值范围是．

查看试题解析
24. 如图，在平面直角坐标系中，函数 $y = - 2 x + 6$ 的图象分别交x轴，y轴于A，B两点，过点A的直线交y轴正半轴于点M，且 $M B = 2 M O$ ．在平面直角坐标系内存在点C，使得以A，B，M，C为顶点的四边形是平行四边形，则点C的坐标为．

查看试题解析

	A款玩偶	B款玩偶
进货价（元/个）	20	15
销售价（元/个）	28	20