云南省玉溪市通海县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x ＞ 2$ B、 $x \geq 2$ C、 $x \leq 2$ D、 $x ＜ 2$

查看试题解析
2. 第24届冬季奥林匹克运动会于2022年2月4日在北京开幕.2022年北京冬奥会会徽以汉字“冬”为灵感来源；北京冬奥会的吉祥物“冰墩墩”是以熊猫为原型进行设计创作；北京冬季残奥会的吉祥物“雪容融”是以灯笼为原型进行设计创作．下列冬奥元素图片中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 (\sqrt{2})^{2} = 12$ C、 $\frac{2}{\sqrt{2}} = 1$ D、 $3 \sqrt{2} \times \sqrt{3} = 3 \sqrt{6}$

查看试题解析
4. 在某校举行的“我的中国梦”演讲比赛中，10名参赛学生的成绩统计如图所示，对于这10名学生的参赛成绩，下列说法中错误的是（）

A、中位数是80 B、众数是80 C、平均数是82 D、极差是40

查看试题解析
5. 直角三角形的两边长分别为a，b，且a，b满足 $\sqrt{a - 3}$ +|b﹣4|＝0，则此三角形的第三长为（　　）

A、5 B、25 C、 $\sqrt{7}$ D、5或 $\sqrt{7}$

查看试题解析
6. 对于一次函数 $y = x - 2$ ，下列结论中正确的是（）

A、函数的图象与x轴交点坐标是 $(0 ， 2)$ B、函数值随自变量的增大而减小 C、函数的图象不经过第二象限 D、函数的图象向下平移2个单位长度得到函数 $y = x$ 的图象

查看试题解析
7. 龟、兔进行m米赛跑，赛跑的路程s（米）与时间t（分钟）的关系如图所示（兔子睡觉前后速度保持不变），根据图像信息，下列说法错误的是（）

A、龟、兔是进行的500米赛跑 B、兔子刚醒来时，乌龟已领先了200米 C、兔子醒来后的赛跑速度是20米/分钟 D、乌龟比兔子早8分钟到达终点

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $∠ A = 60 °$ ， $A B = 7 c m$ ， D是 $A C$ 的中点，则 $B D$ 的长为（）

A、7.5 $c m$ B、7 $c m$ C、6.5 $c m$ D、6 $c m$

查看试题解析
9. 如图，在平行四边形 $A B C D$ 中， $D E$ 平分 $∠ A D C$ ， $A D = 8$ ， $B E = 3$ ，则 $C D =$ （）

A、5 B、6 C、7 D、8

查看试题解析
10. 如图，直线 $y = x + 2$ 与直线 $y = a x + 4$ 相交于点 $P (m ， 3)$ ，则关于 $x$ 的不等式 $x + 2 < a x + 4$ 的解集为（）

A、 $x > 1$ B、 $x < 1$ C、 $x > 3$ D、 $x < 3$

查看试题解析
11. 如图所示为一种“羊头"形图案.其作法如下：从正方形①开始，以它的一边为斜边向外作等腰直角三角形，然后再以等腰直角三角形的直角边为边.分别向外作正方形②和②……依此类推，若正方形①的面积为64，则正方形⑤的面积为（）

A、 $2$ B、 $4$ C、 $6$ D、 $16$

查看试题解析
12. 如图，正方形 $A B C D$ 的边长为8，点M在 $D C$ 上，且 $D M = 2$ ， N是 $A C$ 上一动点，则 $D N + M N$ 的最小值为（）．

A、8 B、 $8 \sqrt{2}$ C、 $2 \sqrt{17}$ D、10

查看试题解析

二、填空题

13. 2022年，新型冠状病毒奥密克我毒株继续肆虐全球，病毒的平均直径约是0.00000009米．数据0.00000009科学记数法表示为．

查看试题解析
14. 袁隆平院士被誉为“世界杂交水稻之父”，他研究的水稻，不仅高产，而且抗倒伏．在某次实验中，他的团队对甲、乙两种水稻品种进行产量稳定实验，各选取了8块条件相同的试验田，同时播种并核定亩产，结果甲、乙两种水稻的平均产量均为1200千克/亩，方差为S_甲²=186.9，S_乙²=325.3．为保证产量稳定，适合推广的品种为

查看试题解析
15. 如图，某景区湖中有一段“九曲桥”连接湖岸A，B两点，“九曲桥”的每一段与AC平行或BD平行，若AB＝100m，∠A＝∠B＝60°，则此“九曲桥”的总长度为．

查看试题解析
16. 若 $a = \sqrt{3} + 1$ ，则代数式 $(1 - \frac{a}{a + 1}) \div \frac{a^{2} - 2 a + 1}{a^{2} - 1}$ 的值为．

查看试题解析
17. 如图，在菱形 $A B C D$ 中，对角线 $A C = 6$ ， $B D = 8$ ，过A点作 $A E ⊥ B C$ ，则 $A E =$ ．

查看试题解析
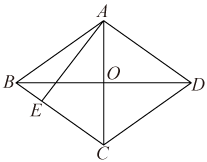18. 在△ABC中，AB=15，AC=13，高AD=12，则 $Δ A B C$ 的周长为．

查看试题解析

三、解答题

19. 《九章算术》是我国古代最重要的数学著作之一，在“勾股”章节中记载了一道“折竹抵地”的问题：“今有竹高一尺，末折抵地，去本三尺，问折者高几何？”译文为：一根竹子，原来高一丈，后来竹子折断，其竹竿恰好着地，着地处离原竹子根部3尺远，问原处还有多高的竹子？翻译成数学问题是：如图所示，△ABC中，∠ACB=90°，AC+AB=10，BC=3，求AC的长．

查看试题解析
20. 新学期，某校开设了“防疫宣传”“心理疏导”等课程，为了解学生对新开设课程的掌握情况，从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级： $A$ 级为优秀， $B$ 级为良好， $C$ 级为及格， $D$ 级为不及格.将测试结果绘制了两幅不完整的统计图.根据统计图中的信息解答下列问题：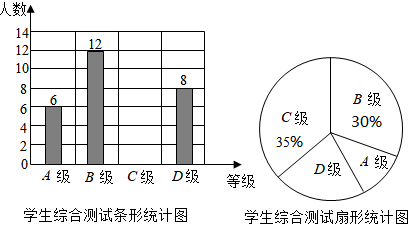

(1)、本次抽样测试的学生人数是名；

(2)、扇形统计图中表示 $A$ 级的扇形圆心角 $α$ 的度数是▲ ，并把条形统计图补充完整；

(3)、该校八年级共有学生400名，如果全部参加这次测试，估计优秀的人数为多少？

查看试题解析
21. 如图，在△ABC中，AB＝AC ，点D、E分别是线段BC、AD的中点，过点A作BC的平行线交BE的延长线于点F ，连接CF ．

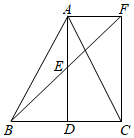(1)、求证：△BDE≌△FAE；

(2)、求证：四边形ADCF为矩形．

查看试题解析
22. 如图，已知过点 $B (1 ， 0)$ 的直线 $l_{1}$ ： $y = k x + b$ （ $k \neq 0$ ）与直线 $l_{2}$ ： $y = 2 x + 4$ ．相交于点 $P (- 1 ， a)$ ．

(1)、求直线 $l_{1}$ 的解析式：

(2)、求 $△ A B P$ 的面积．

查看试题解析
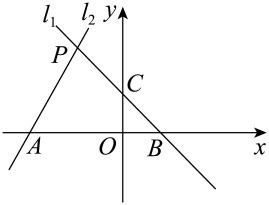23. 某商场计划购进一批篮球和足球，其中篮球的单价比足球多30元．已知用360元购进的足球和用480元购进的篮球数量相等．

(1)、问篮球和足球的单价各是多少元？

(2)、若篮球的售价为150元，足球的售价为110元，商场计划用不超过10350元购进两种球共100个，其中篮球不少于40个，问商场共有几种购货方案？哪种方案商场获利最大，并求出最大利润？

查看试题解析
24. 阅读理解：我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形．如图1，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，依次连接各边中点得到中点四边形EFGH．

(1)、判断图1中的中点四边形EFGH的形状，并说明理由；

(2)、当图1中的四边形ABCD的对角线添加条件时，这个中点四边形EFGH是矩形；四边形ABCD的对角线添加条件时，这个中点四边形EFGH是菱形．

(3)、如图2，在四边形ABCD中，点M在AB上且△AMD和△MCB为等边三角形，E、F、G、H分别为AB、BC、CD、AD的中点，试判断四边形EFGH的形状，并证明你的结论．

查看试题解析