云南省西双版纳傣族自治州2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 的算术平方根是( )A、9 B、3 C、 D、2. 下列各组数中,能成为直角三角形的三条边长的是( )A、3,5,7 B、5,7,8 C、1, ,2 D、4,6,73. 下列运算中,正确的是( )A、 B、 C、 D、4. 在中,点是斜边上的中点,连接 . 若 , 则( ).A、22° B、68° C、96° D、112°5. 某校八年级有8个班,每个班50名学生,为了调查该校八年级学生期末的数学成绩情况,下列抽取方法具有代表性的是( )A、随机抽取一个班的学生 B、随机抽取50名男生 C、随机抽取50名女生 D、从8个班中,随机抽取50名学生6. 如图,在四边形中,对角线与相交于点O,要使四边形为平行四边形,则添加的条件可以是( )
 A、AB//CD, B、 C、 D、7. 将直线向下平移1个单位长度后的直线解析式为( )A、 B、 C、 D、8. “冰墩墩”热潮持续不断,店家为合理进行资金分配,对上月各类型的爆款数量进行数据统计分析,从而确定各款商品批发数量,此时店家应重点参考( )A、众数 B、平均数 C、中位数 D、方差9. 对于函数的图象,下列结论错误的是( )A、经过第二、三、四象限 B、与y轴交于点 C、y随x的增大而减小 D、当时,10. 一根竖直的竹竿于离地面3米处折断,倒下部分与地面成角,这根竹竿在折断前的长度为( )A、6米 B、9米 C、12米 D、1.93米11. 本周末,小明一家从家出发开车前往湿地公园游玩,经过加油站时,加满油后继续驶往目的地,汽车行驶路程y(千米)与汽车行驶时间x(分钟)之间的关系如图所示,下列说法正确的是( )
A、AB//CD, B、 C、 D、7. 将直线向下平移1个单位长度后的直线解析式为( )A、 B、 C、 D、8. “冰墩墩”热潮持续不断,店家为合理进行资金分配,对上月各类型的爆款数量进行数据统计分析,从而确定各款商品批发数量,此时店家应重点参考( )A、众数 B、平均数 C、中位数 D、方差9. 对于函数的图象,下列结论错误的是( )A、经过第二、三、四象限 B、与y轴交于点 C、y随x的增大而减小 D、当时,10. 一根竖直的竹竿于离地面3米处折断,倒下部分与地面成角,这根竹竿在折断前的长度为( )A、6米 B、9米 C、12米 D、1.93米11. 本周末,小明一家从家出发开车前往湿地公园游玩,经过加油站时,加满油后继续驶往目的地,汽车行驶路程y(千米)与汽车行驶时间x(分钟)之间的关系如图所示,下列说法正确的是( ) A、汽车经过25分钟到达加油站 B、汽车加油时长为40分钟 C、汽车加油前的速度比加油后快 D、小明家距离湿地公园80千米12. 如图,点E、F分别是正方形的边上的点,且相交于点G,下列结论错误的是( )
A、汽车经过25分钟到达加油站 B、汽车加油时长为40分钟 C、汽车加油前的速度比加油后快 D、小明家距离湿地公园80千米12. 如图,点E、F分别是正方形的边上的点,且相交于点G,下列结论错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 函数y= 中,自变量x的取值范围是 .14. 如图,在中, , D、E分别是的中点,连接 , 则的长为 .
 15. 已知正比例函数的图象经过点 , 则k的值为 .16. 一艘帆船由于风向的原因先向正东方向航行了16km,然后向正北方向航行了12km,这时它离出发点有km.17. 已如 , . 则 .18. 在平面直角坐标系中,点A、B、C的坐标分别是 , 点D是x轴上的点,若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标是 .
15. 已知正比例函数的图象经过点 , 则k的值为 .16. 一艘帆船由于风向的原因先向正东方向航行了16km,然后向正北方向航行了12km,这时它离出发点有km.17. 已如 , . 则 .18. 在平面直角坐标系中,点A、B、C的坐标分别是 , 点D是x轴上的点,若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标是 .三、解答题
-
19. 计算:.20. 湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.
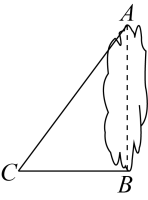
求:
(1)、两棵景观树之间的距离;(2)、点B到直线AC的距离.21. 在平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点B,且的面积为18.(1)、求一次函数的解析式;(2)、点C在直线上,且 , 求点C的坐标.22. 某校为了调查学生平均每天的睡眠时间,在全校随机抽取了20名学生进行调查,并将收集到的学生平均每天睡眠时间t(小时)统计如下表:睡眠时间t(小时)
6
6.5
7
7.5
8
8.5
人数(人)
2
2
4
4
6
2
(1)、求这组数据的众数、平均数、中位数;(2)、请估计该校1500名学生平均每天睡眠时间超过8小时(含8小时)的人数.23. 某学校要购买甲、乙两种消毒液,用于预防新型冠状病霉.若购买9桶甲消毒液和6桶乙消毒液,则一共需要615元:若购买8桶甲消毒液和12桶乙消毒液,则一共需要780元.(1)、每桶甲消毒液、每桶乙消毒液的价格分别是多少元?(2)、若该校计划购买甲、乙两种消毒液共30桶,其中购买甲消毒液a桶,且甲消毒液的数量至少比乙消毒液的数量多5桶,又不超过乙消毒液的数量的2倍.怎样购买.才能使总费用W最少?并求出最少费用,24. 如图,在Rt中, , D是的中点,E是的中点,过点A作AF//BC交延长线于点F.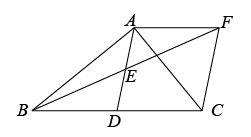 (1)、求证:;(2)、求证:四边形是菱形;(3)、若 , 菱形的面积为10,求的长.
(1)、求证:;(2)、求证:四边形是菱形;(3)、若 , 菱形的面积为10,求的长.