云南省普洱市景谷傣族彝族自治县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{a}$ 的最小值为（）

A、0 B、1 C、 $- 1$ D、不能确定

查看试题解析
2. 自动测温仪仅记录的图象如图所示，它反映了某市的春季某一天气T（℃）如何随时间t（时）的变化而变化的．下列从图象中得到的信息正确的是（）

A、最高气温是零上8℃ B、最低气温是零下4℃ C、0点时气温达到最低 D、0点到14点之间气温持续上升

查看试题解析
3. 甲、乙、丙、丁四位同学3次数学成绩的平均分都是120分，方差分别是 $S_{甲}^{2} = 8.6$ ， $S_{乙}^{2} = 2.6$ ， $S_{丙}^{2} = 5.0$ ， $S_{丁}^{2} = 7.2$ ．则这四位同学3次数学成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 下列二次根式中，可以与 $\sqrt{3}$ 合并的二次根式是（）

A、 $\sqrt{12}$ B、 $\sqrt{18}$ C、 $\sqrt{24}$ D、 $\sqrt{45}$

查看试题解析
5. 以下列线段为边，不能构成直角三角形的是（）

A、1，1， $\sqrt{2}$ B、4，5，6 C、6，8，10 D、9，40，41

查看试题解析
6. 下列运算，结果正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $3 + \sqrt{2} = 3 \sqrt{2}$ C、 $\sqrt{6} \div \sqrt{2} = 3$ D、 $\sqrt{6} \times \sqrt{2} = 2 \sqrt{3}$

查看试题解析
7. 下列各点中，在一次函数 $y = 3 x + 1$ 的图象上的点为（）．

A、 $(3 ， 5)$ B、 $(2 ， 7)$ C、 $(2 ， - 2)$ D、 $(4 ， 9)$

查看试题解析
8. 如图，在一束平行光线中插入一张对边平行的纸板，如果光线与纸板右下方所成的 $∠ 1 = 72 °$ ，则光线与纸板左上方所成的 $∠ 2$ 的度数是（）

A、 $144 °$ B、 $118 °$ C、 $72 °$ D、 $68 °$

查看试题解析
9. 若矩形 $A B C D$ 的邻边长分别是1，2，则 $B D$ 的长是（）

A、 $\sqrt{3}$ B、3 C、 $\sqrt{5}$ D、 $2 \sqrt{5}$

查看试题解析
10. 正比例函数 $y = - \frac{1}{2} x$ 的图象经过的象限是（）

A、第一、三象限 B、第二、四象限 C、第三、四象限 D、第一、二象限

查看试题解析
11. 观察下列等式： $2^{1} = 2$ ， $2^{2} = 4$ ， $2^{3} = 8$ ， $2^{4} = 16$ ， $2^{5} = 32$ ， $2^{6} = 64$ ， $\cdot \cdot \cdot$ ，根据这个规律，则 $2^{1} + 2^{2} + 2^{3} + 2^{4} + \cdot \cdot \cdot + 2^{2022}$ 的末尾数字是（）

A、 $0$ B、 $2$ C、 $4$ D、 $6$

查看试题解析
12. 四边形 $A B C D$ 是菱形， $∠ B A D = 60 °$ ， $A B = 6$ ，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，点 $E$ 在 $A C$ 上，若 $O E = \sqrt{3}$ ，则 $C E =$ （）

A、 $4 \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $4 \sqrt{3}$ 或 $2 \sqrt{3}$ D、4

查看试题解析

二、填空题

13. 当x时，二次根式 $\sqrt{x + 1}$ 在实数范围内有意义．

查看试题解析
14. 如图是小明某一天测得的7次体温情况的折线统计图，这组数据的中位数是．

查看试题解析
15. 数学实践活动中，为了测量校园内被花坛隔开的A，B两点的距离，同学们在AB外选择一点C，测得AC， BC两边中点的距离DE为10m（如图），则A，B两点的距离是 m．

查看试题解析
16. 将一次函数 $y = 3 x - 1$ 的图象沿y轴向上平移3个单位，所得函数表达式．

查看试题解析
17. 如图是一次函数 $y = m x + n$ 的图象，则关于x的方程 $m x + n = 0$ 的解是．

查看试题解析
18. 如图，在 $△ A B C$ 中，按以下步骤作图：①分别以点 $B$ 和 $C$ 为圆心，以大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧相交于点 $M$ 和 $N$ ；②作直线 $M N$ 交边 $A B$ 于点 $E$ ．若 $A C = 5$ ， $B E = 4$ ， $∠ B = 45 °$ ，则 $A B$ 的长为．

查看试题解析

三、解答题

19. 如图，在 $▱ A B C D$ 中，连接BD，点E、F在线段BD上，连接AE、EC、CF、FA．

(1)、请你添加一个条件：，使四边形AECF是平行四边形；（只填一个）

(2)、根据已知及（1）中你所添加的条件，证明：四边形AECF是平行四边形．

查看试题解析
20. 某居民小区有块形状为矩形 $A B C D$ 的绿地，长 $B C$ 为 $\sqrt{128}$ 米，宽 $A B$ 为 $\sqrt{50}$ 米，现在要矩形绿地中修建两个形状大小相同的长方形花坛（即图中阴影部分），每个长方形花坛的长为 $(\sqrt{13} + 1)$ 米，宽为 $(\sqrt{13} - 1)$ 米．

(1)、求矩形 $A B C D$ 的周长．（结果化为最简二次根式）

(2)、除去修建花坛的地方，其它地方全修建成通道，通道上要铺上造价为6元/平方米的地砖，要铺完整个通道，则购买地砖需要花费多少元？

查看试题解析
21. 我县某校响应教体局号召，开展了向贫困学校捐书的活动，为了解学生的捐书量，采用随机抽样的方法抽取30名学生作为样本，对他们的捐书量进行统计，统计结果共有4本，5本，6本，7本，8本五类，分别用A，B，C，D，E表示，根据统计数据绘制成了如图所示的不完整的条形统计图，由图中给出的信息解答下列问题：

(1)、补全条形统计图；

(2)、这30名学生捐书本数的众数为；

(3)、计算这30名学生捐书本数的平均数，并估计该校八年级300名学生共捐书多少本？

查看试题解析
22. 如图，在菱形ABCD中，对角线AC，BD相交于点O，E是CD的中点，连接OE.过点C作CF//BD交OE的延长线于点F，连接DF.
求证：

(1)、△ODE≌△FCE；

(2)、四边形OCFD是矩形．

查看试题解析
23. 如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 $y$ （千瓦时）关于已行驶路程 $x$ （千米）的函数图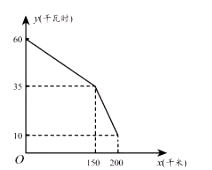象.

(1)、根据图象，直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程，当 $0 \leq x \leq 150$ 时，求1千瓦时的电量汽车能行驶的路程；

(2)、当 $150 \leq x \leq 200$ 时求 $y$ 关于 $x$ 的函数表达式，并计算当汽车已行驶180千米时，蓄电池的剩余电量.

查看试题解析
24. 如图所示，在平面直角坐标系中，已知一次函数 $y = \frac{1}{2} x + 1$ 的图象与 $x$ 轴， $y$ 轴分别交于 $A$ ， $B$ 两点，以 $A B$ 为边在第二象限内作正方形 $A B C D$ ．

(1)、求正方形 $A B C D$ 的面积；

(2)、求点 $C$ ， $D$ 的坐标；

(3)、在 $x$ 轴上是否存在点 $M$ ，使 $Δ M D B$ 的周长最小？若存在，请求出点 $M$ 的坐标；若不存在，请说明理由．

查看试题解析