云南省昆明市西山区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 下列各式中是最简二次根式的是( )A、 B、 C、 D、2. 斜边长是4的直角三角形,它的两条直角边可能是( )A、3, B、2,3 C、3,5 D、2,23. 下列关于矩形的说法错误的是( )A、对角线平分且相等 B、四个角都是直角 C、有四条对称轴 D、是中心对称图形4. 估计 的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间5. 一组数据为:1,7,4,1,4,7,4.则这组数据的众数和中位数分别是( )A、4,1 B、4,2.5 C、7,4 D、4,46. 下列各点中,在一次函数的图象上的点为( ).A、 B、 C、 D、7. 如图,在平行四边形ABCD中,∠A+∠C=140°,则∠B的度数为( )
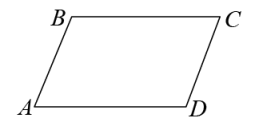 A、140° B、120° C、110° D、100°8. 勾股定理是中国几何的根源,中华数学的精髓,诸如开方术、方程术、天元术等技艺的诞生与发展,寻根探源,都与勾股定理有着密切关系,在一次数学活动中,数学小组发现如下图形:在中, , 图中以AB、BC、AC为边的四边形都是正方形,并且经测量得到三个正方形的面积分别为225、400、S,则S的值为( )
A、140° B、120° C、110° D、100°8. 勾股定理是中国几何的根源,中华数学的精髓,诸如开方术、方程术、天元术等技艺的诞生与发展,寻根探源,都与勾股定理有着密切关系,在一次数学活动中,数学小组发现如下图形:在中, , 图中以AB、BC、AC为边的四边形都是正方形,并且经测量得到三个正方形的面积分别为225、400、S,则S的值为( )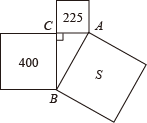 A、25 B、175 C、600 D、6259. 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
A、25 B、175 C、600 D、6259. 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( ) A、20kg B、25kg C、28kg D、30kg10. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若菱形的周长为16,OE的长为( )
A、20kg B、25kg C、28kg D、30kg10. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若菱形的周长为16,OE的长为( )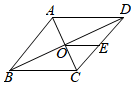 A、2 B、1 C、4 D、311. 若一个函数 中, 随 的增大而增大,且 ,则它的图象大致是( )A、
A、2 B、1 C、4 D、311. 若一个函数 中, 随 的增大而增大,且 ,则它的图象大致是( )A、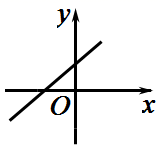 B、
B、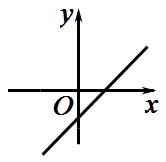 C、
C、 D、
D、 12. 在学习“勾股数”的知识时,爱思考的小琪同学发现了一组有规律的勾股数,并将它们记录在如下的表格中,则当a=18时,b+c的值为( )
12. 在学习“勾股数”的知识时,爱思考的小琪同学发现了一组有规律的勾股数,并将它们记录在如下的表格中,则当a=18时,b+c的值为( )a
6
8
10
12
14
…
b
8
15
24
35
48
…
c
10
17
26
37
50
…
A、242 B、200 C、188 D、162二、填空题
-
13. 若 有意义,则 的取值范围是.14. 在东京奥运会比赛前,有甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表,则这四人成绩最好且发挥最稳定的是 .
选手
甲
乙
丙
丁
平均数(环)
9.4
9.4
9.2
9.2
方差(环2)
0.035
0.015
0.025
0.027
15. 如图,一次函数的图象交x轴于点 , 则关于x的不等式的解集为 . 16. 如图,在中, , 点D是AB的中点, , , 则 .
16. 如图,在中, , 点D是AB的中点, , , 则 .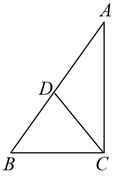 17. 若一次函数的图象向下平移3个单位后经过点 , 则b的值为 .18. 如图,在平面直角坐标系中,的顶点B在x轴上,点A坐标为 , 以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E,再分别以点D,点E为圆心,以大于的长为半径作弧,两弧在∠AOB内相交于点F,作射线OF交AC于点P.则点P的坐标是 .
17. 若一次函数的图象向下平移3个单位后经过点 , 则b的值为 .18. 如图,在平面直角坐标系中,的顶点B在x轴上,点A坐标为 , 以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E,再分别以点D,点E为圆心,以大于的长为半径作弧,两弧在∠AOB内相交于点F,作射线OF交AC于点P.则点P的坐标是 .
三、解答题
-
19. 计算(1)、(2)、20. 2022年4月16日,“太空出差三人组”翟志刚、王亚平、叶光富乘坐神舟十三号载人飞船返回船安全回到地球.神舟十三号乘组共在轨飞行183天,创造了中国航天员连续在轨飞行时间的最长纪录.为了增进学生对航天知识的了解,某校举行了以“航空知识”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取若干名学生的竞赛成绩进行整理和分析(成绩得分用x表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.
竞赛成绩分组统计表:
组别
竞赛成绩分组
频数
平均分
A
8
65
B
a
75
C
20
88
D
b
95

请根据以上信息,解答下列问题:
(1)、a=;b=;m=;(2)、随机抽取的这些学生竞赛成绩的平均分是分;(3)、若学生竞赛成绩达到80分以上(含80分)为优秀,请你估计全校1200名学生中成绩优秀的人数.21. 如图,在△ABC中,AB=13,BC=12,AC=5,点D是BC上一点,且CD=3.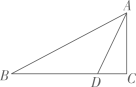 (1)、试判断△ABC的形状,并说明理由;(2)、求AD的长.22. 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)、试判断△ABC的形状,并说明理由;(2)、求AD的长.22. 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E. (1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.23. 某地区以移动互联和大数据技术支持智慧课堂,实现学生的自主、个性和多元学习,全区学生逐步实现上课全部使用平板电脑.某公司根据市场需求代理甲,乙两种型号的平板,每台甲型平板比每台乙型平板进价多600元,用6万元购进甲型平板与用4.5万元购进乙型平板的数量相等.(1)、求每台甲型、乙型平板的进价各是多少元?(2)、该公司计划购进甲,乙两种型号的平板共80台进行试销,其中甲型平板为m台,购买资金不超过17.76万元.并且甲型平板不少于乙型平板的2倍,试销时甲型平板每台售价2800元,乙型平板每台售价2400元,问该公司有几种进货方案?并求出这几种方案中,销售完后获得的利润W的最大值.24. 如图1,在平面直角坐标系中,直线:与x轴交于点 , 与y轴交于点 , 经过原点的直线与直线交于点C.
(1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.23. 某地区以移动互联和大数据技术支持智慧课堂,实现学生的自主、个性和多元学习,全区学生逐步实现上课全部使用平板电脑.某公司根据市场需求代理甲,乙两种型号的平板,每台甲型平板比每台乙型平板进价多600元,用6万元购进甲型平板与用4.5万元购进乙型平板的数量相等.(1)、求每台甲型、乙型平板的进价各是多少元?(2)、该公司计划购进甲,乙两种型号的平板共80台进行试销,其中甲型平板为m台,购买资金不超过17.76万元.并且甲型平板不少于乙型平板的2倍,试销时甲型平板每台售价2800元,乙型平板每台售价2400元,问该公司有几种进货方案?并求出这几种方案中,销售完后获得的利润W的最大值.24. 如图1,在平面直角坐标系中,直线:与x轴交于点 , 与y轴交于点 , 经过原点的直线与直线交于点C. (1)、若 , , 求直线的函数表达式;(2)、在(1)的条件下,当点C的横坐标为1时,求的面积;(3)、当上时,如图2,若OC的长为h,求证 .
(1)、若 , , 求直线的函数表达式;(2)、在(1)的条件下,当点C的横坐标为1时,求的面积;(3)、当上时,如图2,若OC的长为h,求证 .