云南省昆明市石林县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$ B、 $3 \sqrt{5} + 2 \sqrt{5} = 5 \sqrt{10}$ C、 $\sqrt{5} \cdot \sqrt{2} = \sqrt{7}$ D、 $\frac{\sqrt{6}}{\sqrt{2}} = \sqrt{3}$

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{8}$ D、 $2 \sqrt{4}$

查看试题解析
3. 下列命题错误的是（）

A、平行四边形的对角线互相平分 B、矩形的对角线相等且互相平分 C、菱形的对角线相等且互相平分 D、正方形的对角线相等且互相垂直平分

查看试题解析
4. 春和第三中学，八年级一班中的7名学生，2022年期末考试数学成绩如下（单位：分）：82、90、72、100、62、82、82．则这组数据的中位数和众数分别是（）

A、90，82 B、72，82 C、82，82 D、100，82

查看试题解析
5. 点 $(- 2 ， y_{1})$ ， $(1 ， y_{2})$ 都在直线 $y = 2 x + 1$ 上，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} > y_{2}$ D、无法确定

查看试题解析
6. 2016年11月23日国务院印发《“十三五”脱贫攻坚规划》，《规划》按照精准扶贫精准脱贫的基本方略，因地制宜，分类施策，效果显著，2022年某市为了解贫困户后续收入是否稳定，则工作人员需了解贫困户收入的（）

A、平均数 B、方差 C、众数 D、频数

查看试题解析
7. 某天学校组织学生到市文化宫参观学习，早上，大客车从学校出发到市文化宫，匀速行驶一段时间后，途中遇到堵车，原地等了一会，然后大客车加快速度行驶，按时到达文化宫参观学习后，大客车匀速行驶返回．其中t表示客车从学校出发后所用的时间，s表示客车离学校的距离．下面能反映s与t的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
8. 若△ABC三边a、b、c满足 $| a - 3 | + {(b - 4)}^{2} + \sqrt{c - 5} = 0$ ，则△ABC的形状是（）

A、直角三角形 B、等腰三角形 C、锐角三角形 D、钝角三角形

查看试题解析
9. 若 $\sqrt{{(m - 2)}^{2}} = 2 - m$ 成立，则m的取值范围是（）

A、 $m > 2$ B、 $m \geq 2$ C、 $m \leq 2$ D、 $m < 2$

查看试题解析
10. 如图，将矩形ABCD沿直线DE折叠，顶点A落在BC边上F处，已知 $B E = 3$ ， $C D = 8$ ，则BF的长为（）

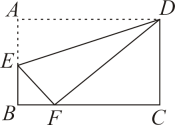A、5 B、4 C、3 D、2

查看试题解析
11. 如图，在菱形ABCD中，对角线AC、BD相交于点O，BE⊥AD于点E，且 $O A = 4$ ， $O B = 3$ ．则BE的长为（）

A、3 B、4 C、4.8 D、5

查看试题解析
12. 如图，某通信公司就使用宽带网推出了E、F、G三种月收费方式，这三种收费方式每月上网时间 $t (h)$ 与所需费用s（元）的函数关系如图所示，则下列判断错误的是（）

A、每月上网时间不足25h时，选择E方式最省钱 B、每月上网费用为70元时，E方式上网时间比F方式多 C、每月上网时间为35h时，选择F方式最省钱 D、每月上网时间超过80h时，选择G方式最省钱

查看试题解析

二、填空题

13. 若二次根式 $\sqrt{3 x - 1}$ 有意义，则x的取值范围是．

查看试题解析
14. 直线 $y = - 2 x + b$ 经过 $(3 ， 2)$ ，则 $b =$ ；

查看试题解析
15. 将一组数据中的每一个数减去30后，得到新的一组数据的平均数是6，则原来这组数据的平均数是；

查看试题解析
16. 如图， $▱ A B C D$ 的对角线AC、BD相交于点O，P是AB边上的中点，且 $O P = 2$ ，则BC的长为；

查看试题解析
17. 如图，在△ABC中，D是AB边上的中点， $∠ A C B = 90 °$ ， $A C = 5$ ， $B C = 12$ ，则 $C D =$ ；

查看试题解析
18. 如图，直线 $y = k x - 3$ 与x轴、y轴分别交于点B与点A， $O B = \frac{1}{3} O A$ ，点C是直线AB上的一点，且位于第二象限，当△OBC的面积为3时，点C的坐标为．

查看试题解析

三、解答题

19. 计算下列各题

(1)、 $2 \sqrt{12} - 9 \sqrt{\frac{1}{3}} + \sqrt{27}$

(2)、 $(\sqrt{3} + 2) (3 - \sqrt{3}) + {(\sqrt{3} + 1)}^{2}$

查看试题解析
20. 如图，BD是 $▱ A B C D$ 的对角线，E、F为BD上两点，且 $B F = D E$ ．求证：四边形AECF是平行四边形．

查看试题解析
21. 某学校为了解学生身高情况，随机抽取了该学校若干名男生、女生进行抽样调查在抽取的样本中男生、女生的人数相同，利用所得数据绘制成如下的统计图表：
根据图表提供的信息，回答下列问题：

(1)、在样本中，男生身高在B组的人数为；

(2)、在样本中，女生身高的众数在组，中位数在组；

(3)、已知该校共有男生500人，女生400人，请估计该校身高在 $155 c m \leq x < 165 c m$ 之间的学生共有多少人？

查看试题解析
22. 如图，在四边形ABCD中， $A B = 12$ ， $B C = 3$ ， $C D = 4$ ， $A D = 13$ ， BC⊥DC于点C．求四边形ABCD的面积．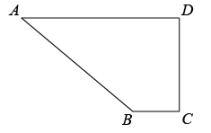

查看试题解析
23. 如图，直线 $y = \frac{3}{2} x - 2$ 与 $y = - x + 3$ 相交于点P，直线 $y = \frac{3}{2} x - 2$ 分别交x轴、y轴于点C、D；直线 $y = - x + 3$ 分别交x轴、y轴于点A、B．

(1)、求两直线交点P的坐标；

(2)、连接BC，求△BCD的面积．

查看试题解析
24. 如图，在四边形ABCD中，AB $∥$ CD， $∠ A B C = 90 °$ ， $A D = C D = 13 c m$ ， $B C = 12 c m$ ， M、N是线段AB、CD上两动点，M点从点A出发，以每秒2cm的速度沿AB方向运动，N点从点D出发，以每秒1cm的速度沿DC方向运动，M、N同时出发，同时停止，当M运动到点B时，M、N同时停止运动，设运动时间为t秒．

(1)、求AB的长；

(2)、当t为何值时，四边形AMCN为平行四边形？

(3)、在M、N运动的过程中，是否存在四边形MBCN是矩形，若存在，请求出的t值；若不存在，请说明理由．

查看试题解析