云南省昆明市盘龙区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
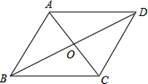
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,四边形ABCD中,对角线AC,BD相交于点O,下列条件能判定四边形ABCD是平行四边形的是( )
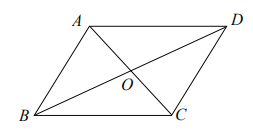 A、 , B、 , C、 , D、 ,4. 函数 中,自变量x的取值范围是( )A、x≠3 B、x≥3 C、x>3 D、x≤35. 为了增强学生的安全意识,某校组织学生开展了安全知识竞赛活动,经过一轮初赛后,共有21人进入决赛,本次活动将按照决赛分数评出一等奖2名,二等奖3名,三等奖5名.小丽进入了决寨,要判断自己能否获奖,她应当关注决赛分数的( )A、平均数 B、众数 C、中位数 D、方差6. 在平面直角坐标系xOy中,直线:与直线:的图象如图所示,则关于x的不等式的解集为( )
A、 , B、 , C、 , D、 ,4. 函数 中,自变量x的取值范围是( )A、x≠3 B、x≥3 C、x>3 D、x≤35. 为了增强学生的安全意识,某校组织学生开展了安全知识竞赛活动,经过一轮初赛后,共有21人进入决赛,本次活动将按照决赛分数评出一等奖2名,二等奖3名,三等奖5名.小丽进入了决寨,要判断自己能否获奖,她应当关注决赛分数的( )A、平均数 B、众数 C、中位数 D、方差6. 在平面直角坐标系xOy中,直线:与直线:的图象如图所示,则关于x的不等式的解集为( )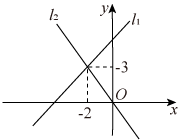 A、 B、 C、 D、7. 如图,在四边形ABCD中,∠B=∠D=90°,分别以四边向外做正方形甲、乙、丙、丁,若用S甲、S乙、S丙、S丁来表示它们的面积,那么下列结论正确的是( )
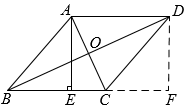
A、 B、 C、 D、7. 如图,在四边形ABCD中,∠B=∠D=90°,分别以四边向外做正方形甲、乙、丙、丁,若用S甲、S乙、S丙、S丁来表示它们的面积,那么下列结论正确的是( )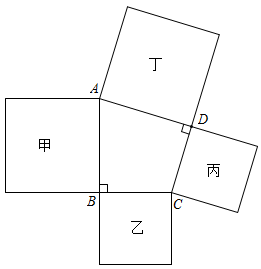 A、S甲= S丁 B、S乙=S丙 C、S甲+S乙=S丙+S丁 D、S甲-S乙=S丙-S丁8. 如图,在四边形ABCD中, , 点E、F分别是AC、AD的中点,且 , 若 , , 则CD的长为( )
A、S甲= S丁 B、S乙=S丙 C、S甲+S乙=S丙+S丁 D、S甲-S乙=S丙-S丁8. 如图,在四边形ABCD中, , 点E、F分别是AC、AD的中点,且 , 若 , , 则CD的长为( )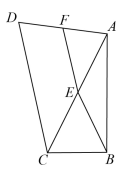 A、 B、 C、 D、89. 已知关于x的一次函数为 , 下列说法中错误的是( )A、若函数图象经过原点,则 B、若 , 则函数图象经过第一、二、三象限 C、函数图象与y轴交于点 D、无论m为何实数,函数图象总经过10. 如图,在矩形ABCD纸片中,E为AD上一点,将沿CE翻折至 . 若点F恰好落在AB上, , , 则( )
A、 B、 C、 D、89. 已知关于x的一次函数为 , 下列说法中错误的是( )A、若函数图象经过原点,则 B、若 , 则函数图象经过第一、二、三象限 C、函数图象与y轴交于点 D、无论m为何实数,函数图象总经过10. 如图,在矩形ABCD纸片中,E为AD上一点,将沿CE翻折至 . 若点F恰好落在AB上, , , 则( )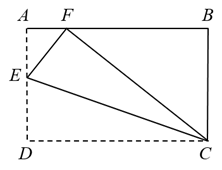 A、5.8 B、5 C、4.8 D、311. 甲、乙两人沿同一条路从A地出发,去往100km外的B地,甲、乙两人离A地的距离s(km)与时间t(h)之间的关系如图所示,以下说法正确的是( )
A、5.8 B、5 C、4.8 D、311. 甲、乙两人沿同一条路从A地出发,去往100km外的B地,甲、乙两人离A地的距离s(km)与时间t(h)之间的关系如图所示,以下说法正确的是( )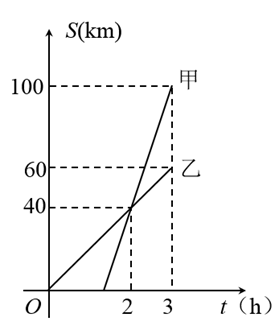 A、甲出发2h后两人第一次相遇 B、甲的速度是20km/h C、甲、乙同时到达B地 D、乙出发或时,甲、乙两人相距20km12. 如图,在正方形ABCD中,AB=4,E为对角线AC上与点A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3,其中正确的结论是( )
A、甲出发2h后两人第一次相遇 B、甲的速度是20km/h C、甲、乙同时到达B地 D、乙出发或时,甲、乙两人相距20km12. 如图,在正方形ABCD中,AB=4,E为对角线AC上与点A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3,其中正确的结论是( )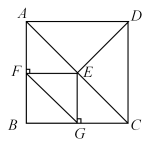 A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
13. 比较大小:14. 为了增强青少年的防毒意识,学校举办了一次“禁毒教育”演讲比赛.某位选手的演讲内容,语言表达,演讲技巧这三项成绩分别为90分,85分,90分,若依次按40%,40%,20%的比例确定最终成绩,则该选手的比赛成绩是分.15. 把直线向上平移5个单位长度,平移后的直线与x轴的交点坐标为 .16. 如图,在菱形ABCD中,对角线AC,BD相交于点O,若AC=6,BD=8,则菱形ABCD的周长是.
 17. 如图,在中, , , , 边在数轴上,以点为圆心,长为半径画弧,交数轴于点 , 则点表示的数是 .
17. 如图,在中, , , , 边在数轴上,以点为圆心,长为半径画弧,交数轴于点 , 则点表示的数是 .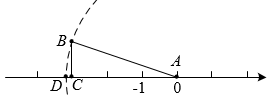 18. 在平面直角坐标系中,对于任意一点 , 我们把点称为点M的“中分对称点”.如图,矩形ABCD的顶点A、B在x轴上,点C的坐标为(2,1),矩形ABCD关于y轴成轴对称.若P在上运动,点Q是点P的“中分对称点”,且点Q在矩形ABCD的一边上,则的面积为 .
18. 在平面直角坐标系中,对于任意一点 , 我们把点称为点M的“中分对称点”.如图,矩形ABCD的顶点A、B在x轴上,点C的坐标为(2,1),矩形ABCD关于y轴成轴对称.若P在上运动,点Q是点P的“中分对称点”,且点Q在矩形ABCD的一边上,则的面积为 .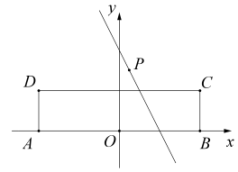
三、解答题
-
19.(1)、;(2)、 .20. 《生物多样性公约》第十五次缔约方大会(COP15)重新确定于2021年5月17日至30日在云南省昆明市举办.“生物多样性”的目标、方法和全球通力合作,将成为国际范围的热点关注内容.为广泛宣传云南生物多样性,某校组织七、八年级各200名学生对《云南的生物多样性》白皮书相关知识进行学习并组织定时测试.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的竞赛成绩,相关数据统计、整理如下:
【收集数据】
七年级10名同学测试成绩统计如下:
72,84,72,91,79,69,78,85,75,95
八年级10名同学测试成绩统计如下:
85,72,92,84,80,74,75,80,76,82
【整理数据】两组数据各分数段,如下表所示:
成绩
七年级
1
5
2
a
八年级
0
4
5
1
【分析数据】两组数据的平均数、中位数、众数、方差如下表:
年级
统计量
平均数
中位数
众数
方差
七年级
80
b
72
66.6
八年级
80
80
c
【问题解决】根据以上信息,解答下列问题:
(1)、填空:a= , b= , c=;(2)、计算八年级同学测试成绩的方差是: . 请估计哪个年级的竞赛成绩更整齐?(3)、按照比赛规定90分及其以上算优秀,请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人?(4)、根据以上数据,你认为该校七、八年级中哪个年级学生知识竞赛成绩更好?请说明理由(至少写出两条理由).21. 阅读下列一段文字,回答问题.【材料阅读】平面内两点M(),N(),则由勾股定理可得,这两点间的距离MN= . 例如,M(3,1),N(1,-2),则MN=
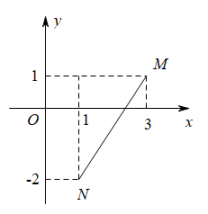
【直接应用】
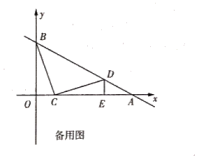
(1)、已知P(2,-3),Q(-1,3),求P、Q两点间的距离;(2)、如图,在平面直角坐标系中,A(-1,-3),OB= , OB与x轴正半轴的夹角是45°.
①求点B的坐标;
②试判断△ABO的形状.
22. 芯片是制造汽车不可或缺的零件,某芯片厂制造的两种型号芯片的成本和批发价如表所示:型号
价格
成本(万元/万件)
批发价(万元/万件)
A
30
34
B
35
40
该厂计划再制造A,B两种型号芯片共30万件,设制造A种型号芯片m万件,制造这批芯片获得的总利润为w万元,
(1)、求这批芯片获得的总利润w(万元)与制造A种型号芯片m(万件)的函数关系式;(2)、若B型号芯片的数量不多于A型号芯片数量的2倍,那么该厂制造A种型号芯片多少件时会获得最大利润,最大利润是多少?