云南省昆明市安宁市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 在函数中,自变量x的取值范围是( )A、 B、 C、且 D、且2. 如图,在中,已知 , , AE平分交BC于点E,则( )
 A、1cm B、2cm C、3cm D、4cm3. 下列无理数中,与相乘积为有理数的是( )A、 B、 C、 D、4. 如图,在正方形ABCD外侧作等边 , 则的度数为( )
A、1cm B、2cm C、3cm D、4cm3. 下列无理数中,与相乘积为有理数的是( )A、 B、 C、 D、4. 如图,在正方形ABCD外侧作等边 , 则的度数为( )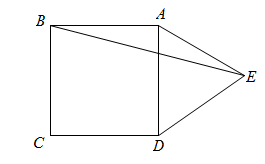 A、15° B、22.5° C、20° D、10°5. 下列数字作为三角形的三边长,不能构成直角三角形的是( )A、8,15,17 B、1, , C、4, , 3 D、 , ,6. 颠球是练习足球球感最基本的招式之一某校足球队10名球员在一次训练中的颠球测试成绩(以“次”为单位计)为:52,50,46,54,50,56,47,52,53,50.则以下数据中计算错误的是( )A、平均数为51 B、方差为8.4 C、中位数为53 D、众数为507. 如图,数轴上的点A对应的实数是-1,点B对应的实数是1,过点B作 , 使 , 连接AC,以点A为圆心,AC为半径画弧交数轴于点D,则点D对应的实数是( )
A、15° B、22.5° C、20° D、10°5. 下列数字作为三角形的三边长,不能构成直角三角形的是( )A、8,15,17 B、1, , C、4, , 3 D、 , ,6. 颠球是练习足球球感最基本的招式之一某校足球队10名球员在一次训练中的颠球测试成绩(以“次”为单位计)为:52,50,46,54,50,56,47,52,53,50.则以下数据中计算错误的是( )A、平均数为51 B、方差为8.4 C、中位数为53 D、众数为507. 如图,数轴上的点A对应的实数是-1,点B对应的实数是1,过点B作 , 使 , 连接AC,以点A为圆心,AC为半径画弧交数轴于点D,则点D对应的实数是( )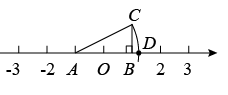 A、 B、 C、 D、8. 如果 ,则a的取值范围是( )A、 B、 C、 D、9. 若 , 则函数的图象可能是( )A、
A、 B、 C、 D、8. 如果 ,则a的取值范围是( )A、 B、 C、 D、9. 若 , 则函数的图象可能是( )A、 B、
B、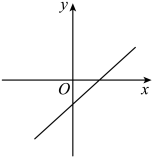 C、
C、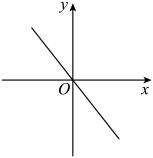 D、
D、 10. 如图,在四边形ABCD中,AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
10. 如图,在四边形ABCD中,AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( ) A、 , B、 , C、 , D、 ,11. 直线y= x+4与x轴、y轴分别交于点A和点B , 点C , D分别为线段AB , OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( ).
A、 , B、 , C、 , D、 ,11. 直线y= x+4与x轴、y轴分别交于点A和点B , 点C , D分别为线段AB , OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( ).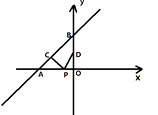 A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)12. 如图,四边形ABCD是正方形,对角线AC、BD相交于点O,点E是AD上除端点外的任意一点,过点O作交CD于点F,若 , 则四边形EOFD的面积为( )
A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)12. 如图,四边形ABCD是正方形,对角线AC、BD相交于点O,点E是AD上除端点外的任意一点,过点O作交CD于点F,若 , 则四边形EOFD的面积为( ) A、18 B、9 C、6 D、不能确定
A、18 B、9 C、6 D、不能确定二、填空题
-
13. 计算: .14. 如图,在中, , , 垂足为D,E是AC的中点,若 , 则 .
 15. 在Rt△ABC中, , 已知AB=15,AC=9,则BC=.16. 如图,直线:与直线:相交于点 , 则关于x的不等式的解集为 .
15. 在Rt△ABC中, , 已知AB=15,AC=9,则BC=.16. 如图,直线:与直线:相交于点 , 则关于x的不等式的解集为 . 17. 如图,O是矩形ABCD对角线AC的中点,E是AB上的一点,将沿CE折叠后,点B恰好与点O重合.若 , 则折痕CE的长为 .
17. 如图,O是矩形ABCD对角线AC的中点,E是AB上的一点,将沿CE折叠后,点B恰好与点O重合.若 , 则折痕CE的长为 . 18. 如图,在四边形ABCD中,对角线AC,BD相交于点O,点E、F、G、H分别是AB、BC、CD、AD的中点,顺次连接E、F、G、H.若 , , 则四边形EFGH的面积为 .
18. 如图,在四边形ABCD中,对角线AC,BD相交于点O,点E、F、G、H分别是AB、BC、CD、AD的中点,顺次连接E、F、G、H.若 , , 则四边形EFGH的面积为 .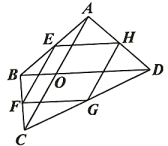
三、解答题
-
19. 计算:(1)、(2)、20. 金方商场日用品柜台10名销售员去年11月完成的销售额情况如下表:
销售额/万元
2
3
5
8
10
售货员/人
2
1
4
2
1
(1)、计算这10名销售员今年3月份销售额的平均数、中位数、众数;(2)、商场为了完成年度销售任务,充分调动销售员的积极性,计划在12月实施超额有奖的计划.根据上面的计算结果,你认为销售员的销售额定为多少比较合适?并说明理由.21. 自2020年以来,安宁市建起了多个“口袋公园”,它们既美化了城市空间,又拓展了市民的公共活动场所,还体现着城市风貌和文化.如图,在某小区旁有一块四边形空地,其中 , , , , . (1)、如图,连接AC,试求AC的长;(2)、安宁市委市政府计划将其打造为“口袋公园”,经测算,每平方米的费用为2000元,请你计算将这块地打造成“口袋公园”需要多少钱?22. 北京冬奥会开启了一场全球瞩目的精彩体育盛事,也让吉祥物“冰墩墩”成为新晋顶流,由于生产厂家产能不足,一度造成“一墩难求”的局面,售价直线上升,随着生产厂家全力协调产能配给,吉样物“冰墩墩”的售价逐渐趋于正常.某玩具商家安排采购员小雷从厂家购进“冰墩墩”、“雪容融”两款毛绒玩具,这两款毛绒玩具的进价和售价如下表:
(1)、如图,连接AC,试求AC的长;(2)、安宁市委市政府计划将其打造为“口袋公园”,经测算,每平方米的费用为2000元,请你计算将这块地打造成“口袋公园”需要多少钱?22. 北京冬奥会开启了一场全球瞩目的精彩体育盛事,也让吉祥物“冰墩墩”成为新晋顶流,由于生产厂家产能不足,一度造成“一墩难求”的局面,售价直线上升,随着生产厂家全力协调产能配给,吉样物“冰墩墩”的售价逐渐趋于正常.某玩具商家安排采购员小雷从厂家购进“冰墩墩”、“雪容融”两款毛绒玩具,这两款毛绒玩具的进价和售价如下表:品名
冰墩墩
雪容融
进价(元/个)
90
75
售价(元/个)
120
100
(1)、第一次小雷用8400元购进了“冰墩墩”、“雪容融”共100个,求“冰墩墩”、“雪容融”各购进多少个?(2)、第二次小雷在进货时,厂家规定“冰墩墩”的进货数量不得超过“雪容融”进货数量的两倍,小雷计划购进两款毛绒玩具共150个.设小雷购进“冰墩墩”m个,售完两款毛绒玩具共获得利润W元,问应如何设计进货方案才能获得最大利润?并求出最大利润.