天津市津南区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x＞﹣2 B、x≥﹣2 C、x≠﹣2 D、x≤﹣2

查看试题解析
2. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{24}$ C、 $\sqrt{5}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
3. 正比例函数y＝﹣1.5x的图象经过（）

A、第一、三象限 B、第二、三象限 C、第一、二象限 D、第二、四象限

查看试题解析
4. 在直角三角形中，斜边长为13，一条直角边长为12，则另一条直角边长为（）

A、3 B、4 C、5 D、6

查看试题解析
5. 在△ABC中，AB＝7，BC＝24，AC＝25，则∠B的大小是（）

A、90° B、60° C、45° D、30°

查看试题解析
6. 数据4，7，4，8，6，6，9，4的众数和中位数是（）

A、6，9 B、4，8 C、6，8 D、4，6

查看试题解析
7. 在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，参加表演的甲、乙两舞团的女演员的身高的平均数均为165，且方差分别为S_甲²＝1.5，S_乙²＝2.5，下列说法正确的是（）

A、乙团的女演员比甲团的女演员的身高整齐 B、甲团的女演员比乙团的女演员的身高整齐 C、两个团的女演员身高一样整齐 D、无法确定哪个团的女演员身高整齐

查看试题解析
8. 下列图标，不能看作中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，在 $▱$ ABCD中，BC＝10，AC＝8，BD＝14，则△AOD的周长是（）

A、18 B、19 C、20 D、21

查看试题解析
10. 如图，四边形ABCD是菱形，对角线AC，BD相交于点O，AB＝5．点E是CD的中点，连接OE，则OE的长是（）

A、2 B、 $\frac{5}{2}$ C、3 D、4

查看试题解析
11. 如图，直线y＝﹣x＋m与y＝nx＋4n（n≠0）的交点的横坐标为﹣3，则关于x的不等式﹣x＋m＞nx＋4n的解集为（）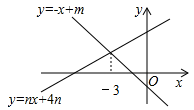

A、x＜﹣3 B、x≤﹣3 C、x＞﹣3 D、x≥﹣3

查看试题解析
12. 在平面直角坐标系中，菱形OABC位置如图所示，B（16，8），则点C的坐标是（）

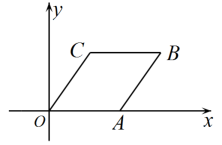A、（6，8） B、（8，6） C、（10，8） D、（8，10）

查看试题解析

二、填空题

13. 计算： $\sqrt{{(- \frac{2}{7})}^{2}}$ ＝； $\frac{\sqrt{3}}{\sqrt{5}}$ ＝．

查看试题解析
14. 某校招聘教师，其中一名教师的笔试成绩是80分，面试成绩是75分，综合成绩的计算方法是笔试成绩占60%，面试成绩占40%，则该教师的综合成绩为分．

查看试题解析
15. 在平面直角坐标系中，将直线y＝3x向下平移2个单位长度．则平移后所得直线的函数解析式是．

查看试题解析
16. 点P（﹣1，﹣ $\sqrt{3}$ ）关于原点的对称点Q的坐标是．

查看试题解析
17. 如图，四边形ABCD和EFGH都是正方形，点E，H分别在AD，CD边上，点F，G在对角线AC上．若AB＝6，则EFGH的面积是．

查看试题解析

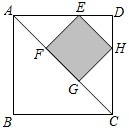
三、解答题

18. 如图，在每个小正方形的边长为1的网格中，点A、点B均为格点．

(1)、AB的长是；

(2)、在网格中，用无刻度的直尺，画出以线段AB为边的矩形ABCD，使它的面积为10，并说明C，D的位置是如何找到的 ▲ ．

查看试题解析
19. 计算：

(1)、 $2 \sqrt{12} - \sqrt{\frac{1}{3}} - \sqrt{27}$

(2)、 $(4 + \sqrt{5}) (4 - \sqrt{5})$

(3)、 $(\sqrt{7} + 2)^{2} + (\sqrt{56} - \sqrt{14}) \div \sqrt{2}$

查看试题解析
20. 如图，E是正方形ABCD的边CD上一点，以点A为中心．把△ADE绕点A逆时针旋转90°，得△ $A D^{'} E^{'}$ ，连接 $E E^{'}$ ．

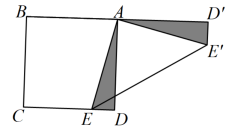(1)、 $∠ E A E^{'}$ 的度数为；

(2)、若AD＝4，DE＝1，求 $E E^{'}$ 的长．

查看试题解析
21. 已知一次函数y＝kx﹣1（k为常数，且k≠0）的图象经过点（3，5）．

(1)、求这个函数的解析式；

(2)、在如图所示的坐标系中画出这个函数的图象；

(3)、当﹣3≤y≤2时，写出x的取值范围．

查看试题解析
22. 已知： $▱$ ABCD的对角线AC、BD相交于点O，E，F分别是OA，OC的中点．

(1)、如图①，求证：DF＝BE；

(2)、如图②，连接DE、BF，求证：四边形DEBF是平行四边形．

查看试题解析
23. 农科院为了解某种小麦的长势，从中随机抽取了部分麦苗，对苗高（单位： $cm$ ）进行了测量．根据统计的结果，绘制出如下的统计图①和图②．

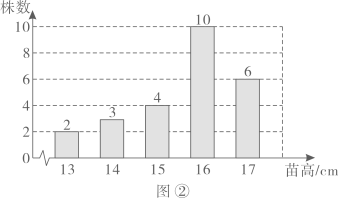
请根据相关信息，解答下列问题：

(1)、本次抽取的麦苗的株数为，图①中m的值为；

(2)、求统计的这组苗高数据的平均数、众数和中位数．

查看试题解析
24. 在 $▱$ ABCD中，对角线AC，BD相交于点O．

(1)、如图①，若OA＝OD，求证： $▱$ ABCD是矩形；

(2)、如图②，若AB＝17，AO＝15，BO＝8，求证▱ABCD是菱形．

查看试题解析
25. 某剧院举行专场音乐会，成人票每张20元，学生票每张5元. 暑假期间，为了丰富广大师生的业余文化生活，影剧院制定了两种优惠方案，方案一：购买一张成人票赠送一张学生票；方案二：按总价的90%付款. 某校有4名老师带队，与若干名（不少于4人）学生一起听音乐会．设学生人数为 $x$ 人， $x \geq 4$ （ $x$ 为整数）．

(1)、根据题意填表：

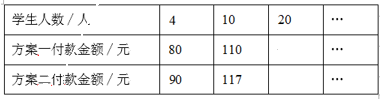(2)、设方案一付款总金额为 $y_{1}$ 元，方案二付款总金额为 $y_{2}$ 元，分别求 $y_{1}$ ， $y_{2}$ 关于 $x$ 的函数解析式；

(3)、根据题意填空：
①若用两种方案购买音乐会的花费相同，则听音乐会的学生有人；
②若有60名学生听音乐会，则用方案购买音乐会票的花费少；
③若用一种方案购买音乐会票共花费了 $450$ 元，则用方案购买音乐会票，使听音乐的学生人数多．

查看试题解析
26. 如图①，在平面直角坐标系中，四边形OACB是正方形，O，B两点的坐标分别是（0，0），（0，6），点C在第一象限，D为OB的中点．

(1)、点C的坐标是，点D的坐标是；

(2)、若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标；

(3)、若E、F为边OA上的两个动点，且EF＝2，当四边形CDEF的周长最小时，直接写出点E、F的坐标．

查看试题解析