山西省太原市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-26 类型：期末考试

进入出卷网下载

一、单选题

1. 分式 $\frac{m + 3}{m - 3}$ 有意义的条件是（）

A、m≠3 B、m≠﹣3 C、m＝3 D、m＝﹣3

查看试题解析
2. 面对新冠病毒疫情，我国毫不动摇坚持动态清零总方针，外防输人，内防反弹，下面是支付宝“国案政务服务平台”中关于疫情防控的四个小程序图标，其中的图案既是轴对称图形，又是中心对称图形的是（）

A、各地疫情风险等级查询 B、扫一扫防疫信息码 C、核酸和抗体检测查询 D、医用口罩信息查询

查看试题解析
3. 如图，四边形ABCD中，AB＝CD．添加下列一个条件后能使四边形ABCD成为平行四边形的是（）

A、AB//CD B、AD//BC C、AB＝BC D、AB＝AC

查看试题解析
4. 下列从左到右的变形，属于因式分解的是（）

A、m²+5m+4＝m（m+5）+4 B、m²﹣4m+4＝（m﹣2）² C、a（m﹣n）＝am﹣an D、15m²n＝3m•5mn

查看试题解析
5. 永寺双塔，又名凌霄双塔，是我市现存最高的古建筑，均为十三层八角形楼阁式砖塔，如图的正八边形是双塔平面示意图，其每个内角的度数为（）

A、80° B、100° C、120° D、135°

查看试题解析
6. 计算 $\frac{1}{x - 1} - \frac{1}{x + 1}$ 的结果是（）

A、 $- 2$ B、 $\frac{2}{x - 1}$ C、 $\frac{2}{x + 1}$ D、 $\frac{2}{x^{2} - 1}$

查看试题解析
7. 如图，△ABC中，∠B＝90°，AB＝BC＝5．现将△ABC沿BC方向平移到△DEF的位置．若平移的距离为3，则CG的长为（）

A、 $3 \sqrt{2}$ B、 $\sqrt{2}$ C、4 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析
8. 将不等式组 ${\begin{array}{l} x + 3 \geq 1 \\ \frac{5 - x}{2} ＜ 1 \end{array}$ 的解集表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
9. 已知四边形ABCD中，对角线AC，BD交于点O．将该四边形绕点O旋转180°，恰好能与原四边形重合，则下列结论不一定正确的是（）

A、OA＝OC，OB＝OD B、AB＝CD C、AC＝BD D、∠ABC＝∠ADC

查看试题解析
10. 2022年5月12日是我国第14个全国防灾减灾日，某校组织防灾减灾教育活动，八年级同学进行了两次地震应急演练，在改进撤离方案后，第二次平均每秒撤离的人数比第一次的多20%，结果360名同学全部撤离的时间比第一次节省了40秒，若设第一次平均每秒撤离x人，则x满足的方程为（）

A、 $\frac{360}{x} = \frac{360}{(1 + 20 %) x} +$ 40 B、 $\frac{360}{x} = \frac{360}{(1 + 20 %) x} -$ 0 C、 $\frac{360}{x} = \frac{360}{20 % x} +$ 40 D、 $\frac{360}{x} = \frac{360}{20 % x} -$ 40

查看试题解析

二、填空题

11. 请写出不等式﹣2x＞4的一个解：．

查看试题解析
12. 如图，已知△ABC中，D，E分别是AB，AC的中点，连接DE并延长至F．使EF＝DE，连接CF．若∠B＝45°，则 $∠ F$ 的度数为．

查看试题解析
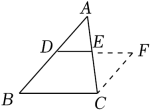13. 已知△A'B'C'是由△ABC平移得到的（点A'，B'，C'分别是A、B、C的对应点），若点A的坐标为（﹣1，2），A'的坐标为（3，4），则点B（﹣3．﹣2）的对应点B'的坐标为．

查看试题解析
14. 如图，四边形ABCD是一个长方形，根据图中所标注的线段长度表示长方形ABCD的面积，可得到的表示一个多项式因式分解的代数恒等式为．

查看试题解析
15. 已知△ABC中．AB＝AC＝5．BC＝2 $\sqrt{5}$ ．如图，将线段AC绕点A逆时针旋转，点C的对应点为D．当∠DAC＝∠CAB时，连接BD，则线段BD的长为．

查看试题解析
16. 已知△ABC中．AB＝AC＝5．BC＝2 $\sqrt{5}$ ．如图．将线段AC绕点C顺时针旋转，点A的对应点为D．当∠ACD＝90°时，连接BD，则线段BD的长为．

查看试题解析

三、解答题

17.

(1)、分解因式：ab³﹣a³b；

(2)、在分解因式时，小彬和小颖对同一道题产生了分歧，下面是他们的解答过程，请认真阅读并完成相应的任务．

题目：将（2x+y）²﹣（x+2y）²分解因式

小彬：原式＝（4x²+4xy+y²）﹣（x²+4xy+4y²）……第1步

＝3x²﹣3y²……第2步

＝3（x+y）（x﹣y）……第3步

小颖：原式＝（2x+y+x+2y）（2x+y﹣x+2y）……第1步

＝（3x+3y）（x+3y）……第2步

＝3（x+y）（x+3y）……第3步

任务：

①经过讨论，他们发现小彬的解答正确，他第1步依据的乘法公式用字母表示为，小颖的解答错误，从第步开始出错，错误的原因是．

②按照小颖的思路，写出正确的解答过程．

查看试题解析

18. 求不等式组 ${\begin{array}{l} 5 - x \geq 3 (x - 1) \\ \frac{2 x - 1}{3} - \frac{5 x + 1}{2} ＜ 1 \end{array}$ 的整数解．

查看试题解析
19.

(1)、先化简，再求值： $\frac{1}{x - 1} \div \frac{x + 2}{x^{2} - 2 x + 1} - \frac{x}{x + 2}$ ，其中x＝﹣4；

(2)、解分式方程： $\frac{4 - x}{3 + x} = \frac{1}{4} + \frac{3}{x + 3}$ ．

查看试题解析
20. 如图，在▱ABCD中，点E、F分别在AD、BC上，且AE＝CF，EF、BD相交于点O，求证：OE＝OF．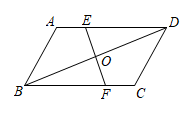

查看试题解析
21. 2022年，是中国共产主义青年团成立100周年，悠悠百年，共青团员始终高举“五四”火炬，坚定不移跟党走，奋力书写属于中国青年的壮丽篇章，为献礼建团百年，山西大剧院音乐厅举行合唱音乐会，校团委组织优秀团员前往观看，已知音乐会票价如下表所示，李老师在订票时，发现甲、丁两类票已售罄，只能选择乙、丙两类，已知李老师一共要订30张票，且总费用不能超过6000元，求他最多能订多少张丙类票？
种类
甲
乙
丙
丁
票价（元/张）
50
180
280
380

查看试题解析
22. 目前，太原结合六城区人口规模与分布、人员流动等因素，优化布设不少于2000个核酸采样点，打造“15分钟核酸检测圈”，免费为群众提供就近检测服务，王叔权家附近有两个核酸采样点，第一次做核酸他步行从家到A采样点，全程1200米；第二次做核酸他慢跑从家到B采样点，比第一次多行了300米，但路上所用时间是第一次的一半，已知王权叔慢跑每分钟比步行每分钟多行120米，求王叔叔慢跑的平均速度．

查看试题解析

23. 综合与实践：

已知，等腰三角形纸片ABC中，AB＝AC，∠BAC＝36°．现要将其剪成三张小纸片，使每张小纸片都是等腰三角形（不能有剩余）．下面是小文借助尺规解决这一问题的过程，请阅读后完成相应任务．

作法：如图1所示，

①分别作AB，AC的垂直平分线，交于点P；

②连接PA，PB，PC．

结论：沿线段PA，PB，PC剪开，即可得到三个等腰三角形，

理由：∵点P在线段AB的垂直平分线上，

∴…….. （依据）．

同理，PA＝PC．

∴PA＝PB＝PC．

∴△PAB、△PBC、△PAC都是等腰三角形

任务：

(1)、上述过程中，横线上的结论为，括号中的依据为．

(2)、受小文的启发，同学们想到另一种思路：如图2，以B为圆心，BC长为半径画弧，交AC于点D，交AB于点E．在此基础上构造两条线段（以图中标有字母的点为端点）作为裁剪线，也可解决问题！请在图2中画出一种裁剪方案，直接写出得到的三个等腰三角形及相应顶角的度数．

(3)、如图3，等腰三角形纸片ABC中，AB＝AC，∠BAC＝108°，请从A，B两题中任选一题作答、我选择题．

A．请在图3中设计出一种裁剪方案，将该三角形纸片分成三个等腰三角形（要求：尺规作图，保留作图痕迹，不写作法，说明裁剪线）．

B．请在图3中设计出一种裁剪方案，将该三角形纸片分成四个等腰三角形，且四个三角形互不全等（要求：尺规作图，保留作图痕迹，不写作法，说明裁剪线）．

查看试题解析

24. 综合与探究：
问题情境：已知，如图1，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4．点D是AC的中点，点E在BC延长线上，且∠CDE＝60°．保持△ABC不动，将△CDE从图1的位置开始，绕点C顺时针旋转α°（0＜α＜180）得到△CD'E'，D、E的对应点分别为D'、E'．

(1)、初步思考：求证：DE＝AC；

(2)、操作探究：如图2，当点 $D^{'}$ 落在DE边上时，连接AD'，判断此时四边形ACE'D'的形状，并说明理由；

(3)、拓展延伸：请从A，B两题中任选一题作答，我选择题．
A．在△CDE旋转过程中，当D'E'//BC时，请直接写出此时旋转角a的度数及B、E'两点间的距离．

B．在△CDE旋转过程中，当D'E'//AB时，延长AC交D'E'于点F，请直接写出此时旋转角α的度数及线段CF的长．

查看试题解析

种类	甲	乙	丙	丁
票价（元/张）	50	180	280	380