山东省枣庄市薛城区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 2022年3月5日,李克强总理在政府工作报告中提出,今年发展主要预期目标之一是粮食产量保持在1.3万亿斤以上.若用x(万亿斤)表示我国今年粮食产量,则x满足的关系为( )A、 B、 C、 D、2. 若分式的值为0,则( )A、 B、 C、 D、3. 如图,边长为a、b的长方形周长为20,面积为16,则a2b+ab2的值为( )
 A、80 B、160 C、320 D、4804. 围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、
A、80 B、160 C、320 D、4804. 围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、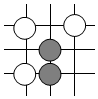 B、
B、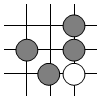 C、
C、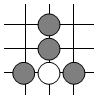 D、
D、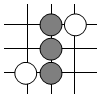 5. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ).
5. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ). A、在 AC、BC 两边高线的交点处 B、在 AC、BC 两边垂直平分线的交点处 C、在 AC、BC 两边中线的交点处 D、在∠A、∠B两内角平分线的交点处6. 如图,平行四边形中, , 是对角线上的两点,如果添加一个条件使四边形是平行四边形,则添加的条件不能是( )
A、在 AC、BC 两边高线的交点处 B、在 AC、BC 两边垂直平分线的交点处 C、在 AC、BC 两边中线的交点处 D、在∠A、∠B两内角平分线的交点处6. 如图,平行四边形中, , 是对角线上的两点,如果添加一个条件使四边形是平行四边形,则添加的条件不能是( ) A、 B、 C、 D、7. 一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )A、360° B、540° C、720° D、900°8. 如图,在中, , , 将绕点C按顺时针方向旋转后得到 , 此时点D在AB边上,则旋转角的大小为( )
A、 B、 C、 D、7. 一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )A、360° B、540° C、720° D、900°8. 如图,在中, , , 将绕点C按顺时针方向旋转后得到 , 此时点D在AB边上,则旋转角的大小为( ) A、20° B、40° C、70° D、50°9. 已知关于x的方程的解是负数,那么m的取值范围是( )A、且 B、且 C、 D、10. 如图,在▱ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CE,CF,EF,则以下四个结论一定正确的是( )
A、20° B、40° C、70° D、50°9. 已知关于x的方程的解是负数,那么m的取值范围是( )A、且 B、且 C、 D、10. 如图,在▱ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CE,CF,EF,则以下四个结论一定正确的是( )
①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边三角形;④CG⊥AE
A、只有①② B、只有①②③ C、只有③④ D、①②③④二、填空题
-
11. 已知 , 则分式的值等于 .12. 要使正十二边形旋转后与自身重合,至少应将它绕中心旋转的度数为13. 不等式组 无解,则m的取值范围 .14. 在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式 , 因式分解的结果是 , 若取 , 时,则各个因式的值是: , , , 于是就可以把“018162”作为一个六位数的密码.对于多项式 , 取 , 时,写出一个用上述方法产生的密码 .15. 枣庄市质检部门抽取甲、乙两厂相同数量的产品进行质量检测,结果甲厂有48件合格产品,乙厂有45件合格产品,甲厂产品的合格率比乙厂高5%,则甲厂产品的合格率为 .16. 如图,一副三角板如图1放置, ,顶点 重合,将 绕其顶点 旋转,如图2,在旋转过程中,当 ,连接 , ,此时四边形 的面积是.

三、解答题
-
17. 分解因式及解方程:(1)、(2)、18. 仔细阅读下面例题,解答问题:
例题:已知二次三项式有一个因式是 , 求另一个因式以及m的值.
解:设另一个因式为 , 则 ,
即 ,
∴ , 解得 .
故另一个因式为 , m的值为-21.
仿照上面的方法解答下面问题:
已知二次三项式有一个因式是x-5,求另一个因式以及k的值.
19. 先化简(1+ )÷ ,再从不等式组 的整数解中选一个合适的x的值代入求值.20. 如图,三角形ABC中任一点P(m,n)经平移后对应点为P1(m+4,n-3),将三角形ABC作同样的平移得到三角形A1B1C1 . (1)、直接写出A1、C1的坐标分别为A1 , C1 ;(2)、在图中画出△A1B1C1;(3)、求出△A1B1C1的面积;(4)、点M在y轴上,若三角形MOC1的面积的面积为6,直接写出点M的坐标 .21. 如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“友好数”.如:①8=32-12;②16=52-32;③24=72-52 , 因此8,16,24 都是“友好数”.(1)、48是“友好数”吗?为什么?(2)、若一个“友好数”能表示为两个连续奇数2k+1和2k-1(k为正整数)的平方差,则这个“友好数”是8的倍数吗?为什么?22. 如图,点D是ABC内一点,点E,F,G,H分别是AB,AC,CD,BD的中点.
(1)、直接写出A1、C1的坐标分别为A1 , C1 ;(2)、在图中画出△A1B1C1;(3)、求出△A1B1C1的面积;(4)、点M在y轴上,若三角形MOC1的面积的面积为6,直接写出点M的坐标 .21. 如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“友好数”.如:①8=32-12;②16=52-32;③24=72-52 , 因此8,16,24 都是“友好数”.(1)、48是“友好数”吗?为什么?(2)、若一个“友好数”能表示为两个连续奇数2k+1和2k-1(k为正整数)的平方差,则这个“友好数”是8的倍数吗?为什么?22. 如图,点D是ABC内一点,点E,F,G,H分别是AB,AC,CD,BD的中点. (1)、求证:四边形EFGH是平行四边形;(2)、如果∠BDC=90°,∠DBC=30°, , AD=6,求四边形EFGH的周长.23. 生活垃圾处理是关系民生的基础性公益事业,加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任.某小区购进A型和B型两种分类垃圾桶,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花30元,购买A型、B型垃圾桶各花费了1800元,且购买A型垃圾桶数量是购买B型垃圾桶数量的1.5倍.(1)、求购买一个A型垃圾桶和一个B型垃圾桶各需多少元?(2)、若小区一次性购买A型和B型垃圾桶共30个,要使总费用不超过2400元,最少要购买多少个A型垃圾桶?24. 如图,平行四边形ABCD中,AE平分交BC于E,DF平分交BC于F.
(1)、求证:四边形EFGH是平行四边形;(2)、如果∠BDC=90°,∠DBC=30°, , AD=6,求四边形EFGH的周长.23. 生活垃圾处理是关系民生的基础性公益事业,加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任.某小区购进A型和B型两种分类垃圾桶,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花30元,购买A型、B型垃圾桶各花费了1800元,且购买A型垃圾桶数量是购买B型垃圾桶数量的1.5倍.(1)、求购买一个A型垃圾桶和一个B型垃圾桶各需多少元?(2)、若小区一次性购买A型和B型垃圾桶共30个,要使总费用不超过2400元,最少要购买多少个A型垃圾桶?24. 如图,平行四边形ABCD中,AE平分交BC于E,DF平分交BC于F. (1)、求证:;(2)、若E为BC的三等分点(靠近C点), , , 求直线AB与CD之间的距离.
(1)、求证:;(2)、若E为BC的三等分点(靠近C点), , , 求直线AB与CD之间的距离.