山东省临沂市费县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-26 类型:期末考试
一、单选题
-
1. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、2. 如果是任意实数,下列各式中一定有意义的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 下列各组数中,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,105. 下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠A=∠C,∠B=∠D C、AB∥CD,AD∥BC D、AB=CD,AD=BC6. 下列描述一次函数 的图象与性质错误的是( )A、点 和 都在此图象上 B、直线与 轴的交点坐标是 C、与正比例函数 的图象平行 D、直线经过一、二、四象限7. 某校在甲、乙两名运动员中,选拔一名参加市运动会100米短跑比赛.分别随机抽取这两名运动员的5次成绩(单位:秒)分析,由甲运动员的成绩 , , 乙运动员的成绩 , , 则最适合参加本次比赛的运动员是( )A、甲 B、乙 C、甲、乙都一样 D、无法选择8. 变量的一些对应值如下表:
…
0
1
2
3
…
…
6
13
20
27
…
根据表格中的数据规律,当x=-5时,的值是( )
A、-29 B、-75 C、41 D、759. 数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得 , 对角线长为 , 改变教具的形状成为图2所示的正方形,则正方形的对角线长为( ) A、 B、 C、 D、10. 如图所示,在平行四边形ABCD中,AB=3.5cm,BC=5cm,AE平分∠BAD,CF∥AE,则AF的长度是( )
A、 B、 C、 D、10. 如图所示,在平行四边形ABCD中,AB=3.5cm,BC=5cm,AE平分∠BAD,CF∥AE,则AF的长度是( )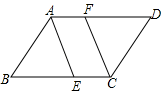 A、1.5cm B、2.5cm C、3.5cm D、0.5cm11. 如图,在菱形ABCD中,对角线AC、BD相交于点O,延长CB至E使BE=CD,连接AE,下列结论①AE=2OD;②∠EAC=90°;③四边形ADBE为菱形;④S四边形AEBO=S菱形ABCD中,正确的结论个数有( )
A、1.5cm B、2.5cm C、3.5cm D、0.5cm11. 如图,在菱形ABCD中,对角线AC、BD相交于点O,延长CB至E使BE=CD,连接AE,下列结论①AE=2OD;②∠EAC=90°;③四边形ADBE为菱形;④S四边形AEBO=S菱形ABCD中,正确的结论个数有( ) A、1个 B、2个 C、3个 D、4个12. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A、1个 B、2个 C、3个 D、4个12. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( ) A、
A、 B、
B、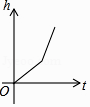 C、
C、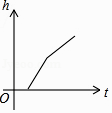 D、
D、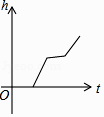
二、填空题
-
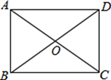
13. 若二次根式 有意义,则x的取值范围是 .14. 如图所示,在矩形ABCD中,AB=2,BD=4,则∠AOB=度 .
 15. 如图,在 的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心, 长为半径作弧,交格线于点D,则 的长为 .
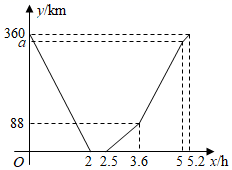
15. 如图,在 的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心, 长为半径作弧,交格线于点D,则 的长为 .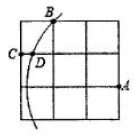 16. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.杜伟同学结合图象得出如下结论:
16. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.杜伟同学结合图象得出如下结论:①快车途中停留了 ;
②快车速度比慢车速度多 ;
③图中 ;
④快车先到达目的地.
其中正确的是.(填序号)
三、解答题
-
17. 计算:(1)、;(2)、 .18. 如图,在中, , , 交边于点 , . 求边的长.
 19. 如图,已知四边形AECF是平行四边形,D,B分别在AF,CE的延长线上,连接AB,CD,且∠B=∠D.
19. 如图,已知四边形AECF是平行四边形,D,B分别在AF,CE的延长线上,连接AB,CD,且∠B=∠D.
求证:
(1)、△ABE≌△CDF;(2)、四边形ABCD是平行四边形.20. 已知:如图,矩形中,对角线、相交于点 , 过 , 两点分别作 , 的平行线,两直线相交于点 . (1)、求证:四边形是菱形;(2)、若 , , 求四边形的周长.21. 为助力新冠肺炎疫情后经济的复苏,天天快餐公司积极投入到复工复产中.现有A、B两家农副产品加工厂到该公司推销鸡腿,两家鸡腿的价格相同,品质相近.该公司决定通过检查质量来确定选购哪家的鸡腿.检察人员从两家分别抽取100个鸡腿,然后再从中随机各抽取10个,记录它们的质量(单位:克)如表:
(1)、求证:四边形是菱形;(2)、若 , , 求四边形的周长.21. 为助力新冠肺炎疫情后经济的复苏,天天快餐公司积极投入到复工复产中.现有A、B两家农副产品加工厂到该公司推销鸡腿,两家鸡腿的价格相同,品质相近.该公司决定通过检查质量来确定选购哪家的鸡腿.检察人员从两家分别抽取100个鸡腿,然后再从中随机各抽取10个,记录它们的质量(单位:克)如表:A加工厂
74
75
75
75
73
77
78
72
76
75
B加工厂
78
74
78
73
74
75
74
74
75
75
(1)、根据表中数据,求A加工厂的10个鸡腿质量的中位数、众数、平均数;(2)、估计B加工厂这100个鸡腿中,质量为75克的鸡腿有多少个?(3)、根据鸡腿质量的稳定性,该快餐公司应选购哪家加工厂的鸡腿?22. 某种机器工作前先将空油箱加满,然后停止加油立即开始工作,当停止工作时,油箱中油量为 .在整个过程中,油箱里的油量y(单位:L)与时间x(单位: )之间的关系如图所示.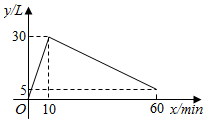 (1)、机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L.(2)、求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.(3)、直接写出油箱中油量为油箱容积的一半时x的值.23. 请你用学习一次函数时积累的经验和方法研究函数的图象和性质,并解决问题.
(1)、机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L.(2)、求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.(3)、直接写出油箱中油量为油箱容积的一半时x的值.23. 请你用学习一次函数时积累的经验和方法研究函数的图象和性质,并解决问题. (1)、根据函数解析式,填写下表:(2)、利用(1)中表格画出函数的图象;(3)、观察图象,当时,随的增大而减小;(4)、利用图象,直接写出不等式的解集.
(1)、根据函数解析式,填写下表:(2)、利用(1)中表格画出函数的图象;(3)、观察图象,当时,随的增大而减小;(4)、利用图象,直接写出不等式的解集.