内蒙古鄂尔多斯市2022年中考数学真题
试卷更新日期:2022-08-26 类型:中考真卷
一、单选题
-
1. 如图,数轴上点A表示的数的相反数是( )
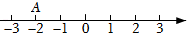 A、﹣2 B、﹣ C、2 D、32. 下列几何体的三视图中没有矩形的是( )A、
A、﹣2 B、﹣ C、2 D、32. 下列几何体的三视图中没有矩形的是( )A、 B、
B、 C、
C、 D、
D、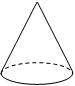 3. 一组数据2,4,5,6,5.对该组数据描述正确的是( )A、平均数是4.4 B、中位数是4.5 C、众数是4 D、方差是9.24. 下列运算正确的是( )A、a3b2+2a2b3=3a5b5 B、(﹣2a2b)3=﹣6a6b3 C、2﹣2=﹣ D、+ =5. 下列尺规作图不能得到平行线的是( )A、
3. 一组数据2,4,5,6,5.对该组数据描述正确的是( )A、平均数是4.4 B、中位数是4.5 C、众数是4 D、方差是9.24. 下列运算正确的是( )A、a3b2+2a2b3=3a5b5 B、(﹣2a2b)3=﹣6a6b3 C、2﹣2=﹣ D、+ =5. 下列尺规作图不能得到平行线的是( )A、 B、
B、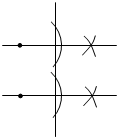 C、
C、 D、
D、 6. 如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为( )
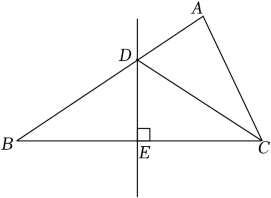
6. 如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为( ) A、2 B、2 C、4 D、4+27. 下列说法正确的是( )
A、2 B、2 C、4 D、4+27. 下列说法正确的是( )①若二次根式有意义,则x的取值范围是x≥1.
②7<<8.
③若一个多边形的内角和是540°,则它的边数是5.
④的平方根是±4.
⑤一元二次方程x2﹣x﹣4=0有两个不相等的实数根.
A、①③⑤ B、③⑤ C、③④⑤ D、①②④8. 实验学校的花坛形状如图所示,其中,等圆⊙O1与⊙O2的半径为3米,且⊙O1经过⊙O2的圆心O2 . 已知实线部分为此花坛的周长,则花坛的周长为( ) A、4π米 B、6π米 C、8π米 D、12π米9. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A、4π米 B、6π米 C、8π米 D、12π米9. 如图,菱形ABCD中,AB=2 , ∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )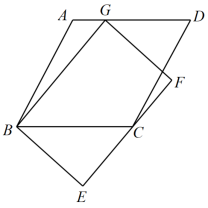 A、 B、 C、 D、310. 如图①,在正方形ABCD中,点M是AB的中点,点N是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为( )
A、 B、 C、 D、310. 如图①,在正方形ABCD中,点M是AB的中点,点N是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为( ) A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
11. 截止2022年1月中国向120多个国家和国际组织提供超20亿剂新冠疫苗,是对外提供此疫苗最多的国家.20亿用科学记数法表示为 .12. 如图,在△ABC中,边BC的垂直平分线DE交AB于点D,连接DC,若AB=3.7,AC=2.3,则△ADC的周长是 .
 13. 按一定规律排列的数据依次为 , , , ……按此规律排列,则第30个数是 .14. 如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE= , 则AB的长是 .
13. 按一定规律排列的数据依次为 , , , ……按此规律排列,则第30个数是 .14. 如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE= , 则AB的长是 . 15. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .
15. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .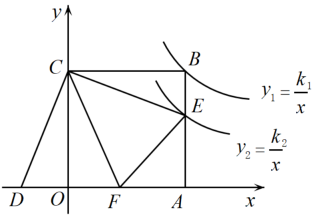 16. 如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
16. 如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .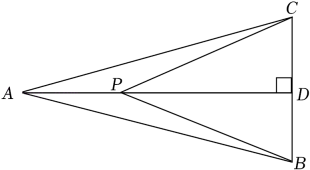
三、解答题
-
17.(1)、解不等式组 , 并写出该不等式组的最小整数解.(2)、先化简,再求值:(+1)÷ , 其中a=4sin30°﹣(π﹣3)0 .18. 为了调查九年级学生寒假期间平均每天观看冬奥会时长情况,随机抽取部分学生进行调查,根据收集的数据绘制了如图所示两幅不完整的统计图
“平均每天观看冬奥会时长”频数分布表
观看时长(分)
频数(人)
频率
0<x≤15
2
0.05
15<x≤30
6
0.15
30<x≤45
18
a
45<x≤60
0.25
60<x≤75
4
0.1
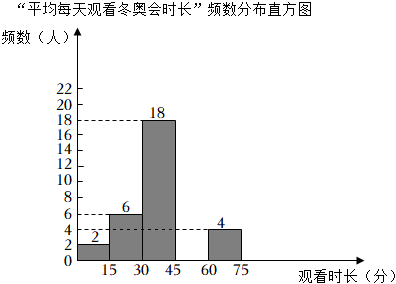 (1)、频数分布表中,a= ▲ , 请将频数分布直方图补充完整;(2)、九年级共有520名学生,请你根据频数分布表,估计九年级学生平均每天观看冬奥会时长超过60分钟的有人;(3)、校学生会拟在甲、乙、丙、丁四名同学中,随机抽取两名同学做“我与冬奥”主题演讲,请用树状图或列表法求恰好抽到甲、乙两名同学的概率.19. 旗杆及升旗台的剖面如图所示,MN、CD为水平线,旗杆AB⊥CD于点B.某一时刻,旗杆AB的一部分影子BD落在CD上,另一部分影子DE落在坡面DN上,已知BD=1.2m,DE=1.4m.同一时刻,测得竖直立在坡面DN上的1m高的标杆影长为0.25m(标杆影子在坡面DN上),此时光线AE与水平线的夹角为80.5°,求旗杆AB的高度.(参考数据:sin80.5°≈0.98,cos80.5°≈0.17,tan80.5°≈6)
(1)、频数分布表中,a= ▲ , 请将频数分布直方图补充完整;(2)、九年级共有520名学生,请你根据频数分布表,估计九年级学生平均每天观看冬奥会时长超过60分钟的有人;(3)、校学生会拟在甲、乙、丙、丁四名同学中,随机抽取两名同学做“我与冬奥”主题演讲,请用树状图或列表法求恰好抽到甲、乙两名同学的概率.19. 旗杆及升旗台的剖面如图所示,MN、CD为水平线,旗杆AB⊥CD于点B.某一时刻,旗杆AB的一部分影子BD落在CD上,另一部分影子DE落在坡面DN上,已知BD=1.2m,DE=1.4m.同一时刻,测得竖直立在坡面DN上的1m高的标杆影长为0.25m(标杆影子在坡面DN上),此时光线AE与水平线的夹角为80.5°,求旗杆AB的高度.(参考数据:sin80.5°≈0.98,cos80.5°≈0.17,tan80.5°≈6) 20. 如图,已知一次函数y=ax+b与反比例函数y=(x<0)的图像交于A(﹣2,4),B(﹣4,2)两点,且与x轴和y轴分别交于点C、点D.
20. 如图,已知一次函数y=ax+b与反比例函数y=(x<0)的图像交于A(﹣2,4),B(﹣4,2)两点,且与x轴和y轴分别交于点C、点D.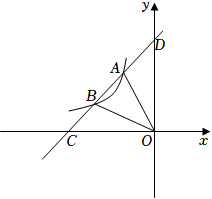 (1)、根据图像直接写出不等式<ax+b的解集;(2)、求反比例函数与一次函数的解析式;(3)、点P在y轴上,且S△AOP=S△AOB , 请求出点P的坐标.21. 如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.
(1)、根据图像直接写出不等式<ax+b的解集;(2)、求反比例函数与一次函数的解析式;(3)、点P在y轴上,且S△AOP=S△AOB , 请求出点P的坐标.21. 如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.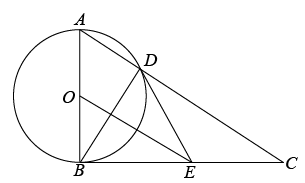 (1)、求证:DE是⊙O的切线;(2)、若DE=5,cos∠ABD= , 求OE的长.22. 某超市采购了两批同样的冰墩墩挂件,第一批花了6600元,第二批花了8000元,第一批每个挂件的进价是第二批的1.1倍,且第二批比第一批多购进50个.(1)、求第二批每个挂件的进价;(2)、两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少?23. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.
(1)、求证:DE是⊙O的切线;(2)、若DE=5,cos∠ABD= , 求OE的长.22. 某超市采购了两批同样的冰墩墩挂件,第一批花了6600元,第二批花了8000元,第一批每个挂件的进价是第二批的1.1倍,且第二批比第一批多购进50个.(1)、求第二批每个挂件的进价;(2)、两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少?23. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.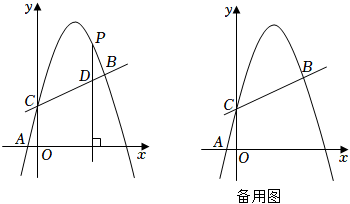 (1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.24. 在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
(1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.24. 在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.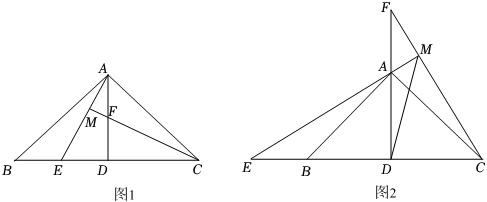 (1)、如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.
(1)、如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.①(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
②连接DM,求∠EMD的度数;
③若DM=6 , ED=12,求EM的长.