辽宁省丹东市2022年中考数学真题
试卷更新日期:2022-08-26 类型:中考真卷
一、单选题
-
1. -7的绝对值是( )A、7 B、-7 C、 D、2. 下列运算正确的是( )A、a2•a3=a6 B、(a2)3=a5 C、(ab)3=a3b3 D、a8÷a2=a43. 如图是由几个完全相同的小正方体组成的立体图形,它的左视图是( )
 A、
A、 B、
B、 C、
C、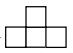 D、
D、 4. 四张不透明的卡片,正面标有数字分别是﹣2,3,﹣10,6,除正面数字不同外,其余都相同,将它们背面朝上洗匀后放在桌面上,从中随机抽取一张卡片,则这张卡片正面的数字是﹣10的概率是( )A、 B、 C、 D、15. 在函数y=中,自变量x的取值范围是( )A、x≥3 B、x≥﹣3 C、x≥3且x≠0 D、x≥﹣3且x≠06. 如图,直线l1//l2 , 直线l3与l1 , l2分别交于A,B两点,过点A作AC⊥l2 , 垂足为C,若∠1=52°,则∠2的度数是( )
4. 四张不透明的卡片,正面标有数字分别是﹣2,3,﹣10,6,除正面数字不同外,其余都相同,将它们背面朝上洗匀后放在桌面上,从中随机抽取一张卡片,则这张卡片正面的数字是﹣10的概率是( )A、 B、 C、 D、15. 在函数y=中,自变量x的取值范围是( )A、x≥3 B、x≥﹣3 C、x≥3且x≠0 D、x≥﹣3且x≠06. 如图,直线l1//l2 , 直线l3与l1 , l2分别交于A,B两点,过点A作AC⊥l2 , 垂足为C,若∠1=52°,则∠2的度数是( ) A、32° B、38° C、48° D、52°7. 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是s甲2=0.12,s乙2=0.59,s丙2=0.33,s丁2=0.46,在本次射击测试中,这四个人成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁8. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A、32° B、38° C、48° D、52°7. 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是s甲2=0.12,s乙2=0.59,s丙2=0.33,s丁2=0.46,在本次射击测试中,这四个人成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁8. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )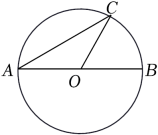 A、6π B、2π C、π D、π9. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a= . 其中正确的有( )
A、6π B、2π C、π D、π9. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a= . 其中正确的有( )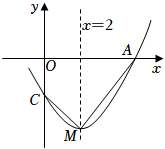 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 美丽的丹东山清水秀,水资源丰富.2021年水资源总量约为12600000000立方米,数据12600000000用科学记数法表示为 .11. 因式分解:2a2+4a+2= .12. 若关于x的一元二次方程x2+3x+m=0有实数根,则m的取值范围是 .13. 某书店与一所中学建立帮扶关系,连续6个月向该中学赠送书籍的数量(单位:本)分别为:200,300,400,200,500,550,则这组数据的中位数是本.14. 不等式组的解集为 .15. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=8,分别以A,C为圆心,以大于AC的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为 .
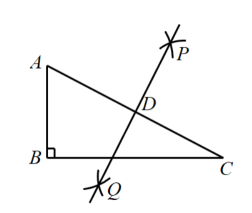 16. 如图,四边形OABC是平行四边形,点O是坐标原点,点C在y轴上,点B在反比例函数y=(x>0)的图象上,点A在反比例函数y=(x>0)的图象上,若平行四边形OABC的面积是7,则k= .
16. 如图,四边形OABC是平行四边形,点O是坐标原点,点C在y轴上,点B在反比例函数y=(x>0)的图象上,点A在反比例函数y=(x>0)的图象上,若平行四边形OABC的面积是7,则k= . 17. 如图,四边形ABCD是边长为6的菱形,∠ABC=60°,对角线AC与BD交于点O,点E,F分别是线段AB,AC上的动点(不与端点重合),且BE=AF,BF与CE交于点P,延长BF交边AD(或边CD)于点G,连接OP,OG,则下列结论:①△ABF≌△BCE;②当BE=2时,△BOG的面积与四边形OCDG面积之比为1:3;③当BE=4时,BE:CG=2:1;④线段OP的最小值为2﹣2 . 其中正确的是 . (请填写序号)
17. 如图,四边形ABCD是边长为6的菱形,∠ABC=60°,对角线AC与BD交于点O,点E,F分别是线段AB,AC上的动点(不与端点重合),且BE=AF,BF与CE交于点P,延长BF交边AD(或边CD)于点G,连接OP,OG,则下列结论:①△ABF≌△BCE;②当BE=2时,△BOG的面积与四边形OCDG面积之比为1:3;③当BE=4时,BE:CG=2:1;④线段OP的最小值为2﹣2 . 其中正确的是 . (请填写序号)
三、解答题
-
18. 先化简,再求值:÷﹣ , 其中x=sin45°.19. 为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2≤t<3,C:3≤t<4,D:t≥4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
 (1)、这次抽样调查共抽取人,条形统计图中的m=;(2)、在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;(3)、已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?(4)、学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.20. 为推动家乡学校篮球运动的发展,某公司计划出资12000元购买一批篮球赠送给家乡的学校.实际购买时,每个篮球的价格比原价降低了20元,结果该公司出资10000元就购买了和原计划一样多的篮球,每个篮球的原价是多少元?21. 如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.
(1)、这次抽样调查共抽取人,条形统计图中的m=;(2)、在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;(3)、已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?(4)、学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.20. 为推动家乡学校篮球运动的发展,某公司计划出资12000元购买一批篮球赠送给家乡的学校.实际购买时,每个篮球的价格比原价降低了20元,结果该公司出资10000元就购买了和原计划一样多的篮球,每个篮球的原价是多少元?21. 如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.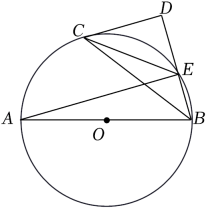 (1)、请判断直线CD与⊙O的位置关系,并说明理由;(2)、若sin∠ECD= , CE=5,求⊙O的半径.22. 如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2nmile(nmile是单位“海里”的符号)处,A港口在B港口北偏西50°方向且距离B港口40nmile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)、请判断直线CD与⊙O的位置关系,并说明理由;(2)、若sin∠ECD= , CE=5,求⊙O的半径.22. 如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2nmile(nmile是单位“海里”的符号)处,A港口在B港口北偏西50°方向且距离B港口40nmile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)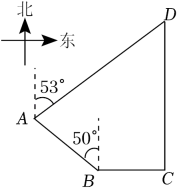 23. 丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
23. 丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:销售单价x(元/件)
…
35
40
45
…
每天销售数量y(件)
…
90
80
70
…
(1)、直接写出y与x的函数关系式;(2)、若每天销售所得利润为1200元,那么销售单价应定为多少元?(3)、当销售单价为多少元时,每天获利最大?最大利润是多少元?24. 已知矩形ABCD,点E为直线BD上的一个动点(点E不与点B重合),连接AE,以AE为一边构造矩形AEFG(A,E,F,G按逆时针方向排列),连接DG.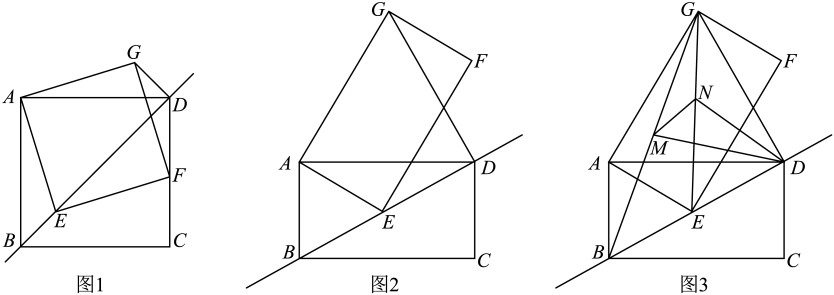 (1)、如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;(2)、如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;(3)、如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB= , ∠AEB=45°,请直接写出△MND的面积.25. 如图1,抛物线y=ax2+x+c(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,点P是第一象限内抛物线上的一个动点,过点P作PD⊥x轴,垂足为D,PD交直线BC于点E,设点P的横坐标为m.
(1)、如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;(2)、如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;(3)、如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB= , ∠AEB=45°,请直接写出△MND的面积.25. 如图1,抛物线y=ax2+x+c(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,点P是第一象限内抛物线上的一个动点,过点P作PD⊥x轴,垂足为D,PD交直线BC于点E,设点P的横坐标为m.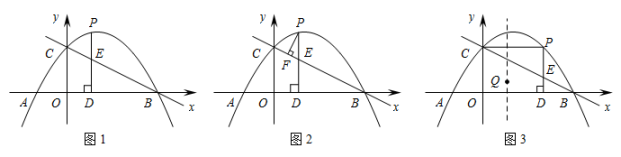 (1)、求抛物线的表达式;(2)、设线段PE的长度为h,请用含有m的代数式表示h;(3)、如图2,过点P作PF⊥CE,垂足为F,当CF=EF时,请求出m的值;(4)、如图3,连接CP,当四边形OCPD是矩形时,在抛物线的对称轴上存在点Q,使原点O关于直线CQ的对称点O′恰好落在该矩形对角线所在的直线上,请直接写出满足条件的点Q的坐标.
(1)、求抛物线的表达式;(2)、设线段PE的长度为h,请用含有m的代数式表示h;(3)、如图2,过点P作PF⊥CE,垂足为F,当CF=EF时,请求出m的值;(4)、如图3,连接CP,当四边形OCPD是矩形时,在抛物线的对称轴上存在点Q,使原点O关于直线CQ的对称点O′恰好落在该矩形对角线所在的直线上,请直接写出满足条件的点Q的坐标.