辽宁省营口市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{x + 3}$ 有意义的条件是（）

A、x>3 B、x>-3 C、x≥3 D、x≥-3

查看试题解析
2. 下列式子计算正确的是（）

A、 $\sqrt{2} - 2 \sqrt{2} = - \sqrt{2}$ B、 $\sqrt{8 a^{2}} = 4 a (a > 0)$ C、 $\sqrt{{(- 5)}^{2}} = - 5$ D、 $\sqrt{6} \div \sqrt{3} = \sqrt{3}$

查看试题解析
3. 如图所示，四边形 $A B C D$ 是平行四边形，点 $E$ 在线段 $B C$ 的延长线上，若 $∠ D C E = 132 °$ ，则 $∠ A =$ （）

A、 $38 °$ B、 $48 °$ C、 $58 °$ D、 $66 °$

查看试题解析
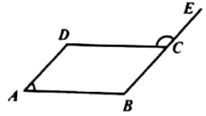4. 如图，在△ABC中，三边a、b、c的大小关系是（）

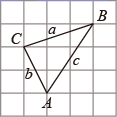A、a<b<c B、c<a<b C、c<b<a D、b<a<c

查看试题解析
5. 如图，在菱形 $A B C D$ 中， $A B = 8$ ， $∠ A D C = 120 °$ ，则 $A C$ 的长为（）

A、8 B、 $4 \sqrt{3}$ C、 $8 \sqrt{3}$ D、4

查看试题解析
6. 某校八年2班5位同学的身高（单位： $cm$ ）组成一组数据为：170、169、172、173、171，则这5位同学身高的平均值（）

A、170 B、171 C、171.5 D、172

查看试题解析
7. 如图，直线 $l_{1}$ ： $y = x + 1$ 与直线 $l_{2}$ ： $y = m x + n$ 相交于点 $P (a ， 2)$ ，则关于x的不等式 $x + 1 \geq m x + n$ 的解集为（）

A、 $x \leq 1$ B、 $x \geq - 1$ C、 $x \geq m$ D、 $x \geq 1$

查看试题解析
8. 如果p(2，m)，A（1，1）,B（4，0）三点在同一条直线，那么m的值为（）

A、2 B、- $\frac{2}{3}$ C、 $\frac{2}{3}$ D、1

查看试题解析
9. 如图，在平面直角坐标系中，点 $A_{1} ， A_{2} ， A_{3}$ …都在x轴上，点 $B_{1} ， B_{2} ， B_{3}$ ⋯都在直线 $y = x$ 上， $△ O A_{1} B_{1} ， △ B_{1} A_{1} A_{2} ， △ B_{2} B_{1} A_{2} ， △ B_{2} A_{2} A_{3} ， △ B_{3} B_{2} A_{3}$ ⋯都是等腰直角三角形，且 $O A_{1} = 1$ ，则点 $B_{2022}$ 的坐标是（）

A、 $(2^{2020} ， 2^{2020})$ B、 $(2^{2021} ， 2^{2021})$ C、 $(2^{2022} ， 2^{2022})$ D、 $(4042 ， 4042)$

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $∠ B C D = 90 °$ ， $A D = A B = 2$ ，点G为 $B C$ 上一点， $D G ∥ A B$ ，且 $D G$ 平分 $∠ B D C$ ，点E为 $B D$ 中点，下面结论：① $B D = 2 C D$ ；② $C D = 2$ ；③ $S_{△ A B D} = 2 S_{△ C D G}$ ；④ $C E ⊥ D G$ ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

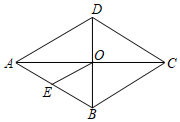
11. 比较大小：3²2³ ．

查看试题解析
12. 正比例函数 $y = (m - 2) x$ 的图象从左到右逐渐下降，则m的取值范围是．

查看试题解析
13. 如图，菱形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O，点E是边 $A B$ 的中点，若 $O E = 4$ ，则 $B C$ 的长为．

查看试题解析
14. 把直线y=x+1沿x轴向右平移2个单位，所得直线的函数解析式为．

查看试题解析
15. 如图， $△ A B H$ 、 $△ C B G$ 、 $△ C D F$ ， $△ D A E$ 是四个全等的直角三角形，如果 $B H = 8$ ， $E G = 2 \sqrt{2}$ ，那么 $A B$ 等于．

查看试题解析
16. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， P是 $B C$ 的中点，M、N分别是 $C A 、 B A$ 延长线上的点，且 $A M = A N = \frac{1}{2} B C$ ，则 $∠ M P N$ 的度数为．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{27} - 3 \sqrt{1 \frac{1}{3}} - \frac{1}{2} \sqrt{48}$ ；

(2)、 $2 \sqrt{12} \times \frac{\sqrt{3}}{4} \div 3 \sqrt{2}$ ．

查看试题解析
18. 某学校在今年母亲节期间开展了“孝顺父母，从家务做起”活动，活动结束后随机调查了八年级部分学生一周在家做家务的时间，并将结果绘制成如图所示两幅不完整的统计图．

请根据统计图提供的信息回答下列问题：

(1)、本次调查的学生总数为人，被调查学生做家务时间的中位数是小时，众数是小时；

(2)、请补全条形统计图；

(3)、若全校八年级共有学生1200人，估计八年级一周在家做家务的时间为5小时的学生有多少人？

查看试题解析
19. 如图，在 $▱ A B C D$ 中，过点D作 $D E ⊥ A B$ 于点E，点F在边 $C D$ 上， $D F = B E$ ，连接 $A F ， B F$ ．

(1)、求证：四边形 $B F D E$ 是矩形；

(2)、若 $C F = 6 ， B F = 8 ， D F = 10$ ，求证： $A F$ 平分 $∠ D A B$ ．

查看试题解析
20. 如图，直线 $y_{1} = x + 2$ 与x、y轴交于点A、B，直线 $y_{2} = k x + 4$ 与x、y轴交于点C、D，两直线相交于点 $E (\frac{2}{3} ， n)$ ．

(1)、求k的值；

(2)、求 $△ A C E$ 的面积．

查看试题解析
21. 如图， $R t △ A B C$ 中， $∠ B = 90 ° ， A B = 12 ， B C = 16 ， C D = 21 ， A D = 29$ ，点E是 $A D$ 的中点，求 $C E$ 的长．

查看试题解析
22. 一辆货车从甲地到乙地，一辆轿车从乙地到甲地，两车沿同一条公路分别从甲、乙两地同时出发，匀速行驶．已知轿车比货车每小时多行驶 $20km$ ．两车相遇后休息一段时间，再同时继续行驶．两车之间的距离 $y (km)$ 与货车行驶时间 $x (h)$ 之间的函数图象如图所示的折线 $A B - B C - C D - D E$ ，结合图象回答下列问题：

(1)、求两车的速度分别是多少 $km/h$ ？

(2)、求线段 $C D$ 的函数关系式．直接写出货车出发多长时间，与轿车相距 $20km$ ？

查看试题解析
23. 在矩形 $A B C D$ 中， $A B = 3 cm ， A D = 9 cm ， B D$ 的垂直平分线分别交 $A D ， B C$ 于点E，F，垂足为O．

(1)、如图1，连接 $B E ， D F$ ，试说明四边形 $B E D F$ 为菱形，并求出它的边长；

(2)、如图2，动点M，N分别从点E，F同时出发，沿 $△ E B A$ 和 $△ F C D$ 各边匀速运动一周，即点M自 $E \to B \to A \to E$ 停止，点N自 $F \to C \to D \to F$ 停止．在运动过程中，已知点M的速度为 $5cm/s$ ，点N的速度为 $4cm/s$ ，设运动时间为 $t s (0 < t < 3)$ ，当以点B，D，M，N四个点为顶点的四边形是平行四边形时，求t的值．

查看试题解析
24. 如图，在正方形 $A B C D$ 中，点P是对角线 $B D$ 上动点，连接 $A P$ 并延长至点E，使 $D E = A B$ ， $A E$ 与 $C D$ 交于点Q．

(1)、求证： $A P = C P$ ；

(2)、若 $∠ P C D = 15 °$
①判断线段 $P C 、 P D 、 P E$ 有怎样的数量关系？并给出证明；

②若AB＝ $\sqrt{6}$ ，请直接写出 $P E$ 的值．

查看试题解析
25. 如图1，直线 $y = \frac{3}{4} x + 6$ 与x，y轴分别交于A，B两点， $∠ A B O$ 的角平分线与x轴相交于点C．

(1)、求点C的坐标；

(2)、在直线 $B C$ 上有两点M，N， $△ A M N$ 是等腰直角三角形， $∠ M A N = 90 °$ ，求点M的坐标；

(3)、点P在y轴上，在平面上是否存在点Q，使以点A、B、P、Q为顶点的四边形为菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析